Luogu 3373

题目链接：https://www.luogu.org/problemnew/show/P3373

题目描述

如题，已知一个数列，你需要进行下面三种操作：

1.将某区间每一个数乘上x

2.将某区间每一个数加上x

3.求出某区间每一个数的和

输入格式：

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2： 格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3： 格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

输出格式： 

输出包含若干行整数，即为所有操作3的结果。

输入样例#1： 

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

输出样例#1： 

17
2

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^）

样例说明：

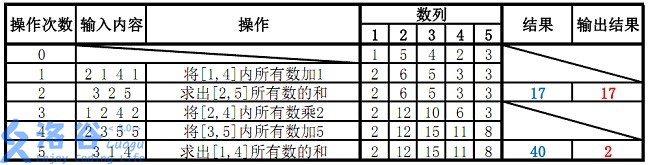
故输出应为17、2（40 mod 38=2）

题解：

由原本的单个的lazy标记变成两个标记：add标记和mul标记，一个记录加，一个记录乘；

需要注意的是，如果同时存在 $add$ 标记和 $mul$ 标记，应当先更新乘法标记，再更新加法标记，也就是说先把 $mul$ 标记pushdown，再把 $add$ 标记pushdown。

同时，由上面pushdown的顺序的缘故可知，当一个节点要乘以 $x$ 时，如果它的 $add$ 标记还存在，记得要把 $add$ 标记也乘 $x$（具体见代码的Update_Mul成员函数）。

（当然，如果你非头铁想要先把 $add$ 标记pushdown，再把 $mul$ 标记pushdown。那么，根据pushdown的顺序，当一个节点要加上 $x$ 时，如果它的 $mul$ 标记还存在，则要把 $x$ 除以 $mul$ 再加到 $add$ 标记上，不过在本题这样一个情况下估计是没法做了……）

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=100000+10;

ll MOD;
int n,m;
ll a[maxn];

/********************************* Segment Tree - st *********************************/
struct Node
{
    int l,r;
    ll val;
    ll add,mul;
    void Update_Mul(ll x)
    {
        val=(val*x)%MOD;
        mul=(mul*x)%MOD;
        add=(add*x)%MOD;
    }
    void Update_Add(ll x)
    {
        val=(val+(r-l+1)*x)%MOD;
        add=(add+x)%MOD;
    }
}node[4*maxn];
void Pushdown(int root)
{
    int ls=root*2, rs=root*2+1;
    if(node[root].mul!=1)
    {
        node[ls].Update_Mul(node[root].mul);
        node[rs].Update_Mul(node[root].mul);
        node[root].mul=1;
    }
    if(node[root].add)
    {
        node[ls].Update_Add(node[root].add);
        node[rs].Update_Add(node[root].add);
        node[root].add=0;
    }
}
void Pushup(int root)
{
    node[root].val=(node[root*2].val+node[root*2+1].val)%MOD;
}
void Build(int root,int l,int r) //对区间[l,r]建树
{
    if(l>r) return;
    node[root].l=l; node[root].r=r;
    node[root].val=0;
    node[root].add=0;
    node[root].mul=1;
    if(l==r) node[root].val=a[l];
    else
    {
        int mid=l+(r-l)/2;
        Build(root*2,l,mid);
        Build(root*2+1,mid+1,r);
        Pushup(root);
    }
}
void Add(int root,int st,int ed,ll val) //区间[st,ed]全部加上val
{
    if(st>node[root].r || ed<node[root].l) return;
    if(st<=node[root].l && node[root].r<=ed) node[root].Update_Add(val);
    else
    {
        Pushdown(root);
        Add(root*2,st,ed,val);
        Add(root*2+1,st,ed,val);
        Pushup(root);
    }
}
void Mul(int root,int st,int ed,ll val) //区间[st,ed]全部加上val
{
    if(st>node[root].r || ed<node[root].l) return;
    if(st<=node[root].l && node[root].r<=ed) node[root].Update_Mul(val);
    else
    {
        Pushdown(root);
        Mul(root*2,st,ed,val);
        Mul(root*2+1,st,ed,val);
        Pushup(root);
    }
}
ll Query(int root,int st,int ed) //查询区间[st,ed]的和
{
    if(st>node[root].r || ed<node[root].l) return 0;
    if(st<=node[root].l && node[root].r<=ed) return node[root].val;
    else
    {
        Pushdown(root);
        ll ls=Query(root*2,st,ed);
        ll rs=Query(root*2+1,st,ed);
        Pushup(root);
        return (ls+rs)%MOD;
    }
}
/********************************* Segment Tree - st *********************************/

int main()
{
    cin>>n>>m>>MOD;
    for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
    Build(1,1,n);

    for(int i=1;i<=m;i++)
    {
        int op; scanf("%d",&op);
        if(op==1)
        {
            int x,y; ll k;
            scanf("%d%d%lld",&x,&y,&k);
            Mul(1,x,y,k);
        }
        if(op==2)
        {
            int x,y; ll k;
            scanf("%d%d%lld",&x,&y,&k);
            Add(1,x,y,k);
        }
        if(op==3)
        {
            int l,r; scanf("%d%d",&l,&r);
            printf("%lld
",Query(1,l,r));
        }
    }
}