循环赛日程表

一、问题描述

设有 n = 2^k 个运动员要进行网球循环赛。现在要设计一个满足以下要求的比赛日程表

1. 每个选手必须与其他 n-1 个选手各赛一场
2. 每个选手一天只能比赛一场
3. 循环赛一共进行 n-1 天

二、算法分析

按此要求可将比赛日程表设计成 n 行 n-1 列的表，在表中第 i 行和第 j 列处填入第 i 个选手在第 j 天所遇到的对手。

按分治策略，可以将所有的选手分为两半，则 n 个选手的比赛日程表可以通过 n/2 个选手的比赛日程表来决定。递归地用一分为二的策略对选手进行划分，直到只剩下两个选手时，比赛日程表的制定就变得很简单，这时只要让这两个选手进行比赛就可以了。

通过 k 增长来看算法实现步骤：

1. 当 k = 1 时，n = 2¹ = 2 人，循环表为

   1　　2

   2　　1

2. 当 k = 2 时，n = 2² = 4 人，循环表为

   1　　2　　3　　4

   2　　1　　4　　3

   3　　4　　1　　2

   4　　3　　2　　1

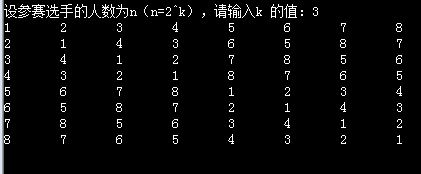
3. 当 k = 3 时，n = 2³ = 8 人，循环表为

   1　　2　　3　　4　　5　　6　　7　　8

   2　　1　　4　　3　　6　　5　　8　　7

   3　　4　　1　　2　　7　　8　　5　　6

   4　　3　　2　　1　　8　　7　　6　　5

   5　　6　　7　　8　　1　　2　　3　　4

   6　　5　　8　　7　　2　　1　　4　　3

   7　　8　　5　　6　　3　　4　　1　　2

   8　　7　　6　　5　　4　　3　　2　　1

以此类推，可以用分治的方法实现，先自顶向下分解，直到分解到最简单的情况，即人数为 2 人，这时就可以两两比赛，表的填充为对角填充的方式，然后再自底向上填充表格，具体的看上面的 k = 1、k = 2、k = 3 时形成的循环表就很好理解了。

三、代码实现

#include <stdio.h>

#define N 64

void GameTable(int k, int a[][N])
{
    int n = 2; // 选手数
    
    // 求解两个选手比赛日，得到左上角元素
    a[0][0] = 1;  a[0][1] = 2;
    a[1][0] = 2;  a[1][1] = 1;
    
    int i, j, half;
    
    // 循环处理，依次处理 2^2 ... 2^k 个选手比赛日程
    for (int t = 1; t < k; t++) {
        
        half = n; // 当前选手数的 1 / 2
        n *= 2;   // 当前选手数
        
        // 左下角
        for (i = half; i < n; i++) // 行
            for (j = 0; j < half; j++) // 列
                a[i][j] = a[i - half][j] + half;
        
        // 右上角
        for (i = 0; i < half; i++)
            for (j = half; j < n; j++)
                a[i][j] = a[i + half][j - half];
        
        // 右下角
        for (i = half; i < n; i++)
            for (j = half; j < n; j++)
                a[i][j] = a[i - half][j - half];
    }
    
    printf("运动员编号	");
    for (i = 1; i < n; i++) {
        printf("第 %d 天	", i);
    }
    printf("

");
    
    for (i = 0; i < n; i++) {
        printf("  %d 号  	", i + 1);
       
        for (j = 1; j < n; j++)
            printf("       %d", a[i][j]);
    
        printf("
");
    }
}

int main()
{
    int a[N][N] = { 0 };
    int k = 3;
    
    printf("******************************************
");
    printf("		**		循环赛日程表		**
");
    printf("******************************************

");
    
    GameTable(k, a);
    
    return 0;
}

******************************************
        **      循环赛日程表      **
******************************************

运动员编号   第 1 天 第 2 天  第 3 天  第 4 天   第 5 天   第 6 天   第 7 天   

  1 号     2       3       4       5       6       7       8
  2 号     1       4       3       6       5       8       7
  3 号     4       1       2       7       8       5       6
  4 号     3       2       1       8       7       6       5
  5 号     6       7       8       1       2       3       4
  6 号     5       8       7       2       1       4       3
  7 号     8       5       6       3       4       1       2
  8 号     7       6       5       4       3       2       1

四、内容来源

算法之循环赛日程表