1,树中的属性操作有:
1,树中结点的数目,树中高度,树的度数;
2,树中结点数目:

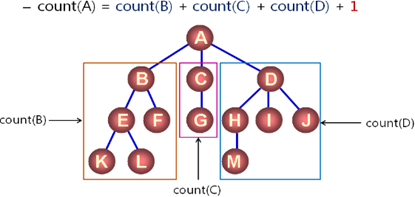
1,定义功能:count(node)
1,在 node 为根结点的树中统计结点数目;
2,递归实现;
2,功能函数代码实现:
1 /* 求以 node 为根结点所代表的树的结点数目,实现的很精妙 */ 2 int count(GTreeNode<T>* node) const // 公有的 count() 函数为 const 函数 3 { 4 int ret = 0; 5 6 if( node != NULL ) // 为空则直接是空树的数目,0;第一种情况;如果 node 没孩子,则 for 循环不会执行,返回 1; 7 { 8 ret = 1; // 至少已经有一个结点,第二种情况 9 10 for(node->child.move(0); !node->child.end(); node->child.next()) // 第三种情况 11 { 12 ret += count(node->child.current()); // 当前结点所拥有的孩子的数目,然后累加 13 } 14 } 15 16 return ret; 17 }
3,树中结点成员函数代码实现:
1 int count() const
2 {
3 return count(root());
4 }
3,树的高度:

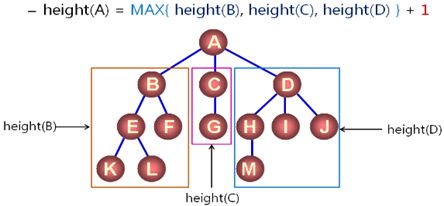
1,定义功能:height(node)
1,获取 node 为根结点的树的高度;
2,递归实现;
2,功能函数代码实现:
1 /* 递归实现以 node 为根结点的树的高度 */ 2 int height(GTreeNode<T>* node) const 3 { 4 int ret = 0; 5 6 if( node != NULL ) // 空树高度为 0 7 { 8 for(node->child.move(0); !node->child.end(); node->child.next()) 9 { 10 int h = height(node->child.current()); // 求当前子树高度 11 12 if( ret < h ) // 遍历查找最大元素 13 { 14 ret = h; 15 } 16 } 17 18 ret = ret + 1; // 子树的高度加上根结点的高度为当前树的高度,包含了二、三两种情况 19 } 20 21 return ret; 22 }
3,树的高度成员函数代码实现:
1 int height() const
2 {
3 return height(root());
4 }
4,树的度数:

1,定义功能:degree(node)
1,获取 node 为根结点的树的度数;
2,递归实现;
2,树的度数功能函数代码实现:
1 /* 递归实现以 node 为结点的树的度数 */ 2 int degree(GTreeNode<T>* node) const 3 { 4 int ret = 0; 5 6 if( node != NULL ) // 空树度数为 0 7 { 8 ret = node->child.length(); // 根结点孩子的数目 9 10 for(node->child.move(0); !node->child.end(); node->child.next()) 11 { 12 int d = degree(node->child.current()); // 每一颗子树都求度数 13 14 if( ret < d ) // 当前度数较小,则保存最新求出来的度数,这里同时也包含了根结点的孩子数目 15 { 16 ret = d; // ret 是度数最大值,即树的度数 17 } 18 } 19 } 20 21 return ret; 22 }
3,树的度数功能函数代码实现:
1 /* 递归实现以 node 为结点的树的度数 */ 2 int degree(GTreeNode<T>* node) const 3 { 4 int ret = 0; 5 6 if( node != NULL ) // 空树度数为 0 7 { 8 ret = node->child.length(); // 根结点孩子的数目 9 10 for(node->child.move(0); !node->child.end(); node->child.next()) 11 { 12 int d = degree(node->child.current()); // 每一颗子树都求度数 13 14 if( ret < d ) // 当前度数较小,则保存最新求出来的度数,这里同时也包含了根结点的孩子数目 15 { 16 ret = d; // ret 是度数最大值,即树的度数 17 } 18 } 19 } 20 21 return ret; 22 }