学习笔记:可持久化线段树(主席树):静态 + 动态
前置知识:
- 线段树。线段树分享可以看:@秦淮岸、@ZYzzz、@妄想の岚がそこに
- 树状数组。(BIT)分享可以看:@T-Sherlock、Chicago、@weishengkun
- 权值线段树:相当于将线段树当成一个桶,其中的每一个点所代表的区间相当于一段值域。维护的值为这段值域中的一些信息。
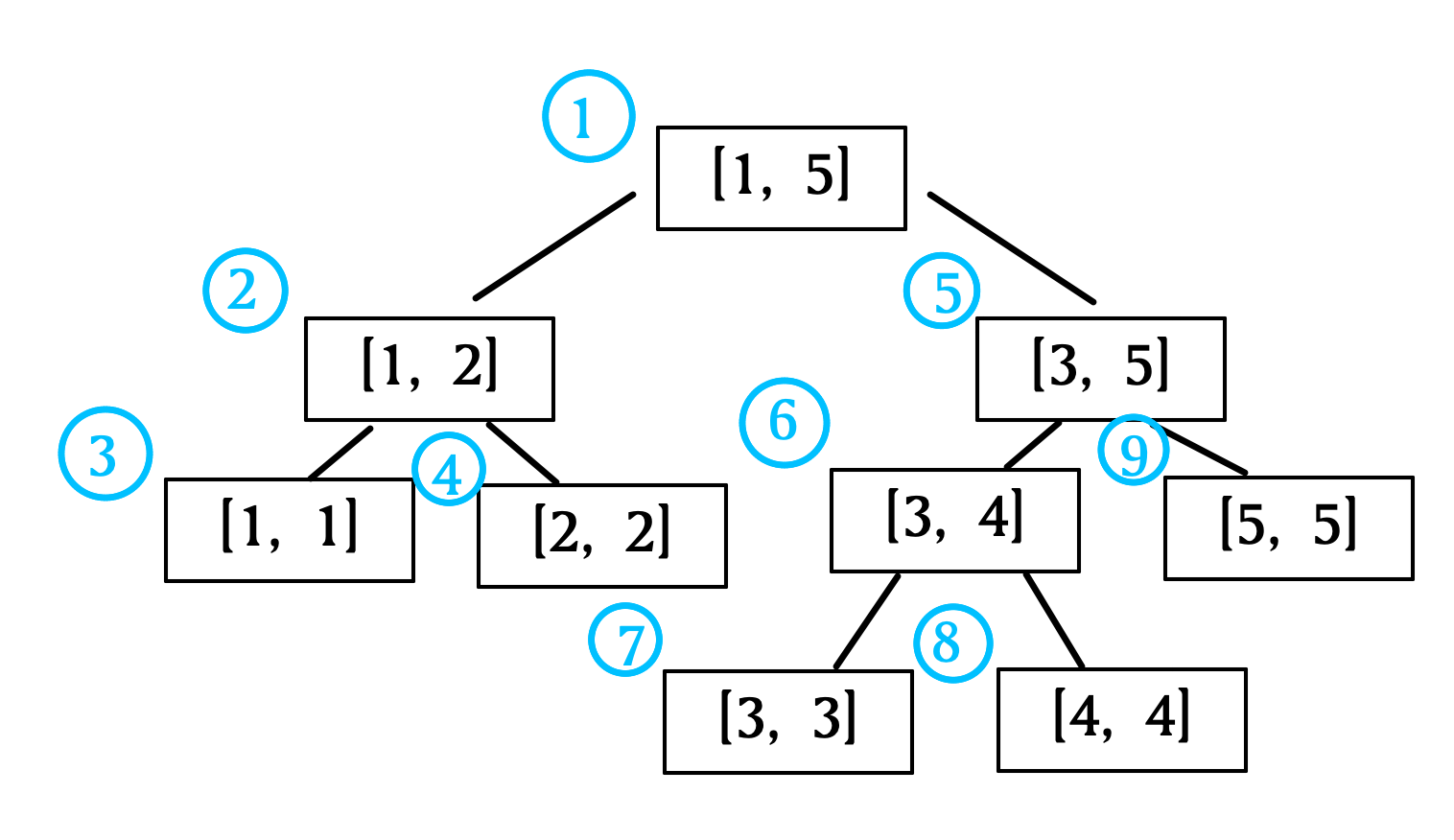
例如该图,节点(2)代表的是值域为([1, 2])的区间,节点(6)代表值域为([3, 4])的区间...
- 可持久化概念:
可持久化实质上就是存储该数据结构所有的历史状态,以达到高效的处理某些信息的目的。
静态区间第(k)小
抛出问题
题目链接:给定长度为(N)的序列(A),有(M)次询问,给定(l_i, r_i, k_i),求在([l_i, r_i])区间内第(k_i)小的数是多少。
(N <= 10^5, M <= 10^4)
先考虑如何求总序列第(k)小
我们可以建立一颗权值线段树,每个点存储的信息为该值域区间存在的数的个数。

因为线段树的性质,所以每个点的左子树的值域区间 $ <= $ 右子树的值域区间。
所以我们先看左子树区间有多少个数,记为(cnt_{left})。
- 如果(k_i <= cnt_{left}),说明第(k_i)小的数一定在左子树的值域内,所以问题便转换为了“在左子树的值域内找第(k_i)小的数”。
- 否则,说明第(k_i)小的数一定在左子树的值域内,考虑到左子树已经有(cnt_{left})个最小的数,问题便转换为了“在右子树的值域内找第(k_i - cnt_{left})小的数”
问题转换到任意区间
我们要用([l_i, r_i]) 区间的数建立权值线段树。
我们发现可以用前缀和来维护:
只要用预处理大法分别以([1, l_i])和([1, r_i])的数建立权值线段树,每个点的值对位相减即可。
关键性质
发现以([1, x])和([1, x + 1])区间内的数所建立的权值线段树的差异仅在一条链上:((A[x + 1])的次数(+1))。
也就是不超过(log_2n)个点。我们可以考虑动态开点:
- 与上一个权值线段树没有差异的地方直接指引过去
- 有差异,单独新增一个点
这样即可预处理出([1, x] (1 <= x <= n))所有的权值线段树了。
时间复杂度(O(nlog_2n)),空间复杂度(O(2n + nlog_2n))。
注意:由于值域很大,我们需要离散化一下。
参考代码:
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100005;
//d 为离散化数组
int n, m, len, a[N], d[N];
//T[i] 为 [1, i] 区间的权值线段树的根节点
int T[N], tot = 0;
//线段树的每个点
struct SegTree{
int l, r, v;
}t[N * 20];
//建树
int build(int l, int r){
int p = ++tot, mid = (l + r) >> 1;
if(l < r) {
t[p].l = build(l, mid);
t[p].r = build(mid + 1, r);
}
t[p].v = 0; return p;
}
//增加一个数 pre 为上一个的根节点。
int update(int pre, int l, int r, int v){
int p = ++tot, mid = (l + r) >> 1;
t[p].l = t[pre].l, t[p].r = t[pre].r, t[p].v = t[pre].v + 1;
if(l < r){
//应该更新哪一个值域区间
if(v <= mid) t[p].l = update(t[pre].l, l, mid, v);
else t[p].r = update(t[pre].r, mid + 1, r, v);
}
return p;
}
//查询
int query(int x, int y, int l, int r, int k){
//找到了
if(l == r) return l;
//对位相减
int sum = t[t[y].l].v - t[t[x].l].v, mid = (l + r) >> 1;
if(k <= sum) return query(t[x].l, t[y].l, l, mid, k);
else return query(t[x].r, t[y].r, mid + 1, r, k - sum);
}
int main(){
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
scanf("%d", a + i), d[i] = a[i];
//离散化
sort(d + 1, d + 1 + n);
len = unique(d + 1, d + 1 + n) - (d + 1);
for(int i = 1; i <= n; i++)
a[i] = lower_bound(d + 1, d + 1 + len, a[i]) - d;
T[0] = build(1, len);
for(int i = 1; i <= n; i++)
T[i] = update(T[i - 1], 1, len, a[i]);
//回答
while(m--){
int l, r, k; scanf("%d%d%d", &l, &r, &k);
int ans = query(T[l - 1], T[r], 1, len, k);
printf("%d
", d[ans]);
}
return 0;
}
动态区间第(k)小
抛出问题
题目链接:
给定长度为(N)的序列(A),有(M)次询问:
- 给定(l_i, r_i, k_i),求在([l_i, r_i])区间内第(k_i)小的数是多少。
- 给定(x_i, val_i),将(A[x_i])的值改为(val_i)。
(N <= 10^5, M <= 10^5)
解决方案:主席树 + 树状数组思路优化
注:这道题也有树套树和整体二分的做法,这里讲解的是主席树 + 树状数组思路优化。
考虑到修改操作对每棵权值线段树的影响是:
- 设修改前的值为(w),则([1, x] (x_i <= x <= n))的线段树都把值域为(w)的点(-1)
- ([1, x] (x_i <= x <= n))的线段树都把值域为(val_i)的点(+1)
这样做的时间复杂度过高,我们可以考虑用树状数组的二进制思想进行优化:
(T[i])这颗线段树代表([i - lowbit(x) + 1, x])这段区间建成的线段树:
- 修改操作,最多修改(log_2n)颗线段树即可。
- 查询操作,用不超过(2 * log_2n)颗线段树就能拼(前缀和)出([l_i, r_i])的线段树。
注意,在查询时的代码实现:
- 用(X)数组存储拼出([1, x - 1])的所有点。
- 用(Y)数组存储拼出([1, y])的所有点。
然后用普通主席树的方法,让所有的跟着跳,对位相减即可。
时间复杂度(O(nlog^2n)), 空间复杂度(O(2n + (n + m)log^2n))
参考代码:
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
//P为最多可能的线段树点数
const int N = 100005, P = N * 441, L = 20;
//操作序列
struct Ops{
int i, j, k;
}op[N];
//线段树
struct SegTree{
int l, r, v;
}t[P];
//d数组为离散化数组
int n, m, len = 0, a[N], d[N << 1];
//T[i] 以 [i - lowbit(x) + 1, x] 这段区间的线段树的根节点
//X[i]、Y[i]代表多个点跟着跳,类似于普通版的$x, y$。
int T[N], tot = 0, X[L], Y[L], cx, cy;
char s[2];
//建树
int build(int l, int r){
int p = ++tot, mid = (l + r) >> 1;
t[p].v = 0;
if(l < r){
t[p].l = build(l, mid);
t[p].r = build(mid + 1, r);
}
return p;
}
//更新
int update(int pre, int l, int r, int x, int v){
int p = ++tot, mid = (l + r) >> 1;
t[p].l = t[pre].l, t[p].r = t[pre].r, t[p].v = t[pre].v + v;
if(l < r){
if(x <= mid) t[p].l = update(t[pre].l, l, mid, x, v);
else t[p].r = update(t[pre].r, mid + 1, r, x, v);
}
return p;
}
//把 [1, i] (x <= i <= n) 的线段树中值域为 a[x] 的次数 += v
void inline add(int x, int v){
int val = lower_bound(d + 1, d + 1 + len, a[x]) - d;
for(; x <= n; x += x & -x)
T[x] = update(T[x], 1, len, val, v);
}
//查询
int query(int l, int r, int k){
if(l == r) return l;
int mid = (l + r) >> 1, sum = 0;
//前缀和
for(int i = 1; i <= cx; i++)
sum -= t[t[X[i]].l].v;
for(int i = 1; i <= cy; i++)
sum += t[t[Y[i]].l].v;
if(k <= sum){
//跟着跳
for(int i = 1; i <= cx; i++)
X[i] = t[X[i]].l;
for(int i = 1; i <= cy; i++)
Y[i] = t[Y[i]].l;
return query(l, mid, k);
}else{
//跟着跳
for(int i = 1; i <= cx; i++)
X[i] = t[X[i]].r;
for(int i = 1; i <= cy; i++)
Y[i] = t[Y[i]].r;
return query(mid + 1, r, k - sum);
}
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
scanf("%d", a + i), d[++len] = a[i];
for(int i = 1; i <= m; i++){
scanf("%s", s);
if(s[0] == 'Q') {
scanf("%d%d%d", &op[i].i, &op[i].j, &op[i].k);
}else{
scanf("%d%d", &op[i].i, &op[i].j);
d[++len] = op[i].j; op[i].k = 0;
}
}
//离散化
sort(d + 1, d + 1 + len);
len = unique(d + 1, d + 1 + len) - (d + 1);
//这里建树,将每一个根节点初始化成1。
T[0] = build(1, len);
for(int i = 1; i <= n; i++)
T[i] = 1;
//建立可持久化线段树
for(int i = 1; i <= n; i++)
add(i, 1);
//处理询问
for(int i = 1; i <= m; i++){
if(op[i].k){
//是查询操作
cx = 0; cy = 0;
//把需要跳的点扔进去
for(int j = op[i].i - 1; j; j -= j & -j)
X[++cx] = T[j];
for(int j = op[i].j; j; j -= j & -j)
Y[++cy] = T[j];
printf("%d
", d[query(1, len, op[i].k)]);
}else{
//修改操作
add(op[i].i, -1);
a[op[i].i] = op[i].j;
add(op[i].i, 1);
}
}
return 0;
}
参考: