引言
排序算法是数据结构和算法之中的基本功,无论是在笔试还是面试,还是实际运用中都有着很基础的地位。这不正直七月,每年校招的备战期,所以想把常见的排序算法记录下来。在本篇文章中的排序算法使用 JavaScript 实现。
一、 冒泡排序
冒泡排序是排序算法中最简单的一个算法,其优点是易理解,易实现。在一些对性能要求不高且数据量不大的需求中,冒泡排序是一个很好的选择。
原理:假设排序顺序为增序,数组长度为 N。数组每相邻两个元素进行比较,大数后移,小数前移,第一轮排序下来就能找到最大的数。也就是比较 A[i] 和 A[i+1] ,将大数后移,随后增加 i 的值,再进行比较。第二轮再对剩余的 N-1 个数进行排序,找出第二大的数,以此类推。同时也可以记录交换次数来进行优化,如果在一层循环之中交换次数为 0,则排序结束。
下面这张图展示了冒泡排序的全过程:

下面这张图展示冒泡排序在宏观层面的全过程:

| 平均时间复杂度 | 最优时间负复杂度 | 最坏时间复杂度 | 空间复杂度 |
| O(n^2) | O(n) | O(n^2) | O(1) |
1 function bubbleSort (arr) { 2 var swapTime = 0; 3 for(var i = 0, length1 = arr.length; i < length1; i ++){ 4 for(var j = 0, length2 = length1 - i; j < length2 - 1; j ++){ 5 if(arr[j] > arr[j+1]){ 6 swapTime++; 7 var temp = arr[j]; 8 arr[j] = arr[j+1]; 9 arr[j+1] = temp; 10 } 11 } 12 //检查交换次数,如果为0,则当前数组为有序数组;如不为0,则重置 13 if(swapTime === 0){ 14 break; 15 }else { 16 swapTime = 0; 17 } 18 } 19 }
二、选择排序
选择排序算法与冒泡排序算法类似,即每一轮找出一个最大值。但和冒泡排序不同的一点是,冒泡排序是采用不停的交换将最大值(最小值)筛选出来,而选择排序是记录下最大值(最小值)的索引。
原理:假设排序方式为增序,数组长度为 N。设置最大值索引初始值 index = 0,然后遍历数组,记录下最大值的索引,即比较 A[i] 与 A[index] 的值,若 A[i] > A[index] 则更新 index = i。在每一轮遍历结束后,交换 index 位置和末尾位置的值,即交换 A[index] 和 A[i],这样便保证了末尾值是最大值。随后对剩余的 N-1 个数进行同样的方式排序,以此类推。
下面这张图展示了选择排序的全过程:
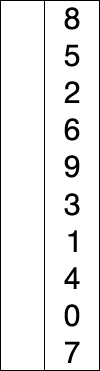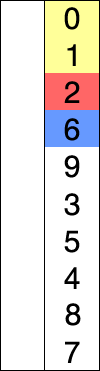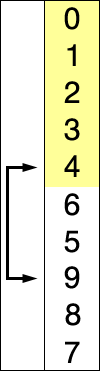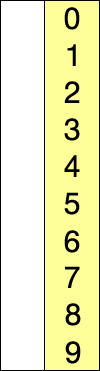
下面这张图展示了在宏观层面上选择排序的全过程:

| 平均时间复杂度 | 最优时间复杂度 | 最差时间复杂度 | 空间复杂度 |
| O(n^2) | O(n^2) | O(n^2) | O(1) |
1 function selectSort (arr) { 2 for(var i = 0, length1 = arr.length; i < length1; i ++){ 3 var index = 0 4 for(var j = 0, length2 = length1 - i; j < length2; j ++){ 5 if(arr[j] > arr[index]){ 6 index = j; 7 } 8 } 9 var temp = arr[index]; 10 arr[index] = arr[length1 - i - 1]; 11 arr[length1 - i - 1] = temp; 12 } 13 }
三、插入排序
插入排序的思想是将原始数组划分成两侧,一侧是有序数组,一侧是无序数组。每次取出无序数组的一个元素,将它插入到有序数组的正确位置上,这种方式也会导致有序数组中其插入位置之后的元素全部后移。插入排序的思想类似于我们抓扑克牌。
原理:假设排序方式为增序,数组长度为 N。初始设 A[0] 为有序数组,A[1] ~ A[N-1] 为无序数组,取出 A[1] 将其插入至有序数组中的正确位置,使得有序数组增大为 A[0] ~ A[1]。继续取 A[2] 将其插入至有序表数组的正确位置,以此类推,直至无序数组取完。
下面这张图展示了插入排序的全过程:

下面这张图展示了在宏观层面上插入排序的全过程:

| 平均时间复杂度 | 最优时间复杂度 | 最差时间复杂度 | 空间复杂度 |
| O(n^2) | O(n^2) | O(n^2) | O(1) |
1 function insertSort (arr) { 2 for(var i = 0, length1 = arr.length; i < length1; i ++){ 3 for(var j = 0, length2 = i + 1; j < length2; j ++){ 4 if(arr[j] > arr[length2]){ 5 var temp = arr[length2]; 6 for(var k = length2; k > j; k --){ 7 arr[k] = arr[k-1]; 8 } 9 arr[j] = temp; 10 } 11 } 12 } 13 }
四、 希尔排序
希尔排序是优化过后的插入,其算法的思想是在插入排序的基础上加上了一个步长 gap,通过步长将数组分成若干个子项,先分别对子项进行插入排序,使得每一个元素朝着最终目的地跨了一大步。然后逐步缩小步长,这种排序算法也是不稳定的。
原理:假设排序方式为增序,数组长度为 N。首先取步长 gap = N/2,那么便将 N 长度的数组拆分成了 [A[0], A[gap]],[A[1], A[gap+1]],[A[2], A[gap+3]] ... ... [A[gap-1], A[N-1]] 子数组,分别对子数组进行插入排序。随后逐步缩小步长,再进行插入排序,直至步长为 1。
下面这张图展示了希尔排序的全过程:
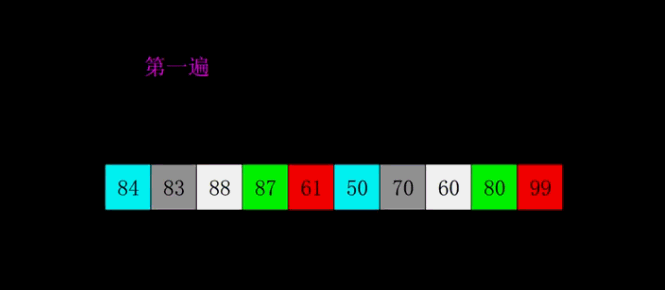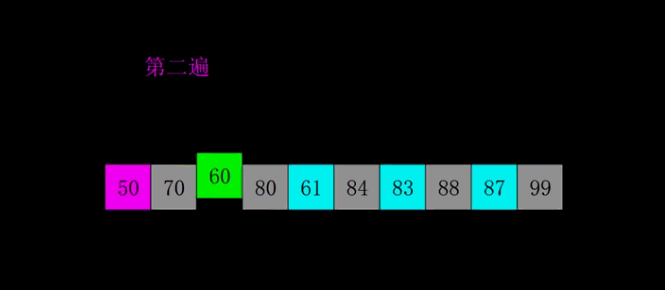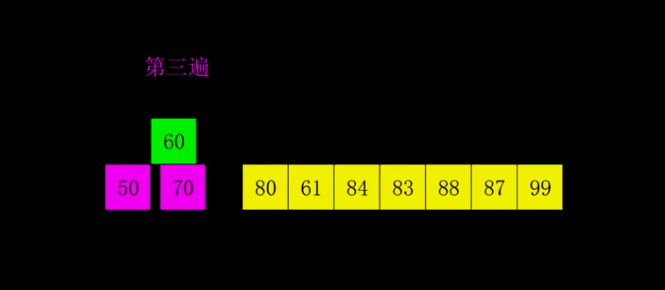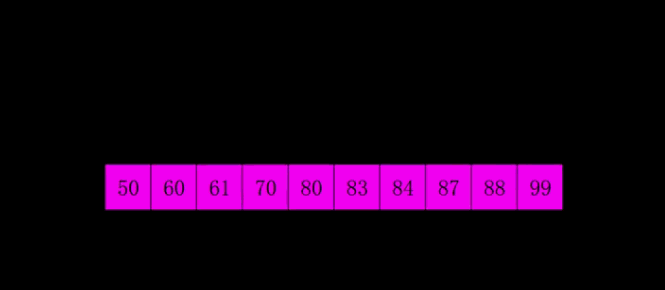
下面这张图展示了希尔排序在宏观上的全过程:

| 平均时间复杂度 | 最优时间复杂度 | 最差时间复杂度 | 空间复杂度 |
| O(nLogn)~O(n^2) | O(n^1.3) | O(n^2) | O(1) |
1 function shellSort(arr) { 2 var gap = Math.floor(arr.length / 2); 3 while (gap >= 1) { 4 for (var i = 0; i < gap; i++) { 5 for (var j = i; j < arr.length; j += gap) { 6 for (var k = i, length = j + gap; k < length; k += gap) { 7 if (arr[k] > arr[length]) { 8 var temp = arr[length]; 9 for (var x = length; x > k; x = x - gap) { 10 arr[x] = arr[x - gap]; 11 } 12 arr[k] = temp; 13 } 14 } 15 } 16 } 17 gap = Math.floor(gap / 2); 18 } 19 }
五、归并排序
归并排序是分治法思想的典型应用,我们可以把一个 N 规模的问题分解成若干个小规模的子问题,用子问题的解来求解原问题。这同时也涉及到了问题的求解顺序,在动态规划算法中有自顶向下和自底向上两种不同的求解顺序。在这里一般采用的是自底向上的求解方法,比如一个 N 长度的数组,我们可以分解成 N/2 个长度为 2 或 1 的子数组,分别对子数组排序,再进行两两相并,直到归并成原始数组。
原理:假设排序顺序为增序,数组长度为 N。将数组拆分成 N 个长度为 1 的数组。然后相邻子数组进行归并,形成若干个长度为 2 或者 1 的数组,再继续进行归并,直至长度为 N。
下面这张图展示了归并的排序的全过程:
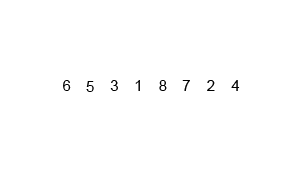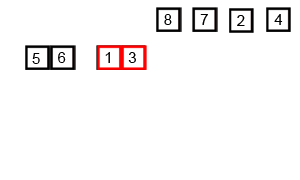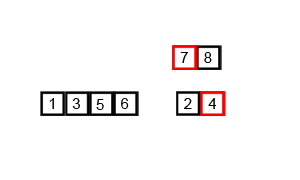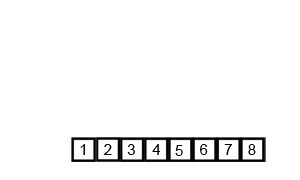
下面这张图展示了在宏观层面上归并排序的全过程:

| 平均时间复杂度 | 最优时间复杂度 | 最差时间复杂度 | 空间复杂度 |
| O(nLogn) | O(nLogn) | O(nLogn) | O(n) |
1 function mergeSort(arr) { 2 var n = 1; 3 while (n < arr.length) { 4 for (var i = 0; i < arr.length; i += n*2) { 5 var arr1 = arr.slice(i, i+n); 6 var arr2 = arr.slice(i+n, i+(n*2)); 7 var temp = []; 8 while(arr1.length != 0 || arr2.length != 0){ 9 if(arr1.length === 0){ 10 temp.push(arr2.shift()); 11 continue; 12 } 13 if(arr2.length === 0){ 14 temp.push(arr1.shift()); 15 continue; 16 } 17 if(arr1[0] < arr2[0]){ 18 temp.push(arr1.shift()); 19 }else{ 20 temp.push(arr2.shift()); 21 } 22 } 23 arr.splice(i, n*2, ...temp); 24 } 25 n = n * 2; 26 } 27 }
六、快速排序
快速排序同样也使用了分治法的思想,在实际运用中使用的最多的就是快速排序。快速排序的核心思想是运用递归法,在每轮排序时指定一个基数,将基数移动到正确的位置上,然后再把基数的左右两边拆分出来,并分别进行相同的排序处理,直到其子数组长度为 1。其采用的是自顶向下的处理法。
原理:在每一轮排序中取一个基数 k , 设 i 和 j 分别为数组的最左端和最右端,i 坐标从起始点向 k 点遍历,若找到一个比 k 大的元素,则停下来等待 j 的遍历。 j 坐标从起始点向 k 点遍历,若找到一个比 k 小的元素,则 i 和 j 坐标的元素互相交换。若有一端提前到达了 k 点,则等待满足条件后与另一端坐标交换。当 i 和 j 碰撞时,则为分治点,此时 i 和 j 相碰撞的坐标元素便是它的最终位置,以碰撞点为中心将数组拆分成两段,并进行相同的递归处理。当 i >= j 时,则为回退点。
下面给出一张维基百科上的图,展示了一轮快速排序的过程:
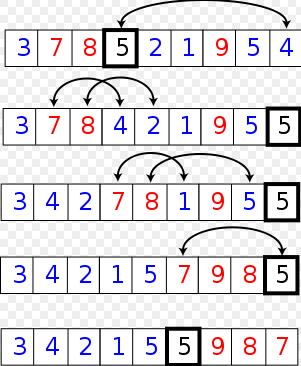
下面这张图展示了一段快速排序的全过程:
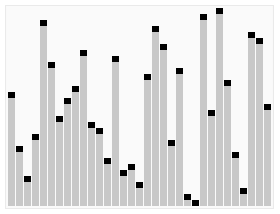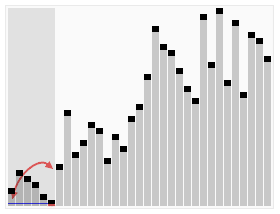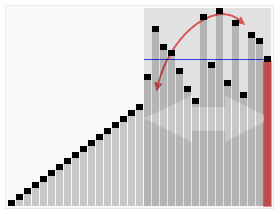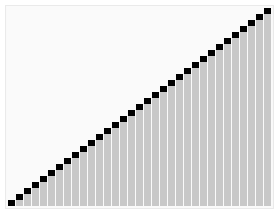
| 平均时间复杂度 | 最优时间复杂度 | 最差时间复杂度 | 空间复杂度 |
| O(nLogn) | O(nLogn) | O(n^2) | O(1) |
1 function quickSort (arr) { 2 function sort(array, first, last) { 3 if (first >= last) { 4 return; 5 } 6 var base = Math.floor((first + last) / 2); 7 var i = first - 1; 8 var j = last - 1; 9 var temp; 10 while (j > i) { 11 while (j > i && array[j] > array[base]) { 12 j--; 13 } 14 while (i < j && array[i] <= array[base]) { 15 i++; 16 } 17 temp = array[i]; 18 array[i] = array[j]; 19 array[j] = temp; 20 } 21 temp = array[base]; 22 array[base] = array[i]; 23 array[i] = temp; 24 sort(array, first, i); 25 sort(array, i + 2, last) 26 } 27 sort(arr, 1, arr.length); 28 }
在这里我们 JavaScript 描绘出快速排序的过程: