「XSection立体几何」游戏简介、平面、截面

Horis International Limited 制作组

最近在玩 Euclidea 的时候，偶然发现，这个制作组在 Google Play 上还有其他的作品：

玩了一圈下来，只有 Euclidea 中的题需要最优解，其他三个都不需要。在这些游戏中，我认为最有意思的是最后一个：XSection。

关于XSection

游戏共有11个章节，121个关卡。每个关卡都是关于立体几何的一道题，需要作图完成。

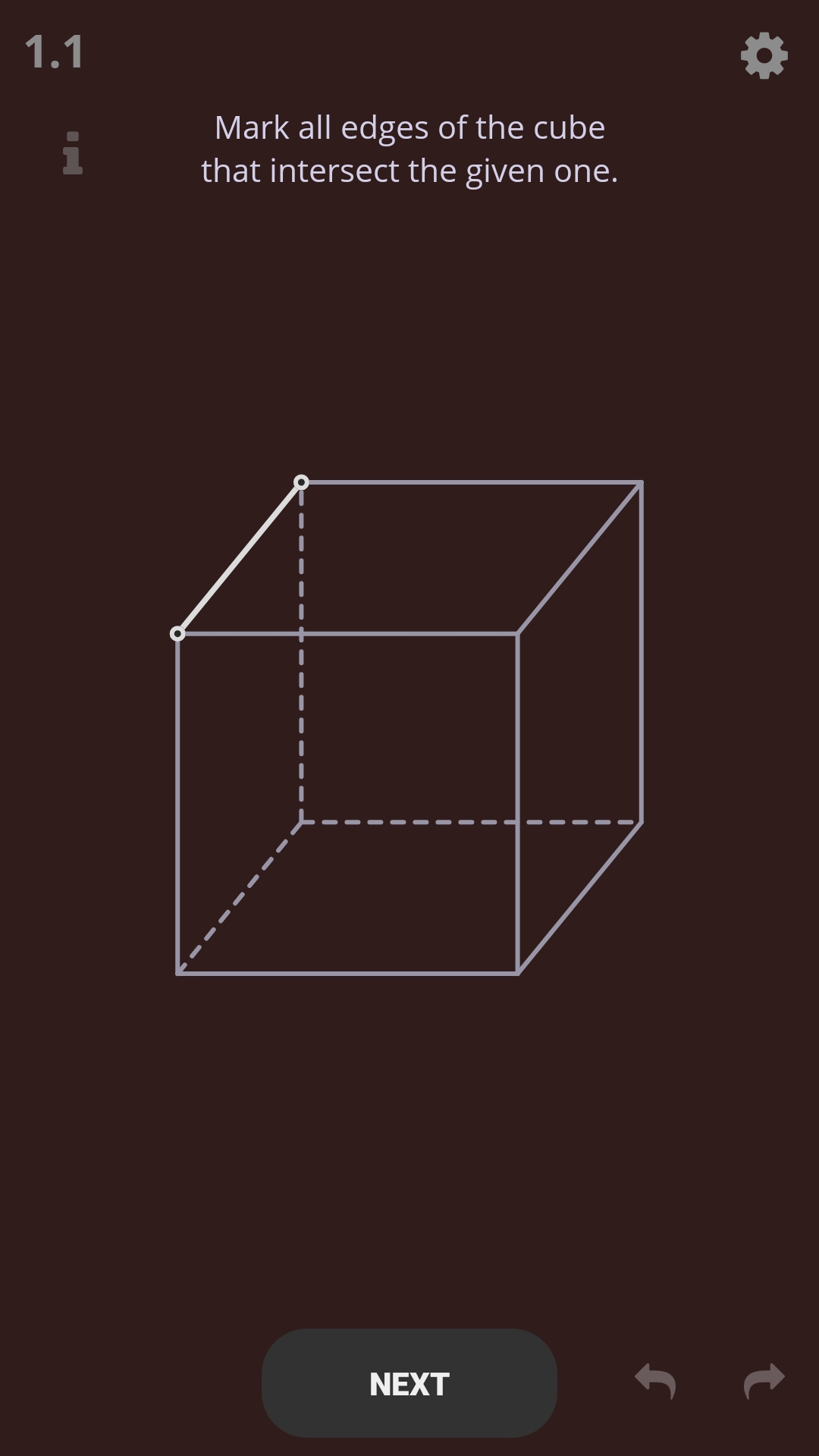
值得注意的是，在整个游戏过程中，你只能进行两种操作：

1. 作过两个点的一条直线（连接两个点）
2. 过一点作一条直线/线段的平行线

这两种操作的存在，使一些问题的解决非常困难。但这两种最基本的操作，是可以解决这里面的所有问题的。

并且，在游戏中，你无法切换视图，只能以设定好的位置观察这个图形，放大或者缩小。

这个游戏并不要求最优解，也就是说，可以尽情放飞自我作图，只要有解法就可以过关。后面的关卡会难一些，需要比较强的空间想象力，并且后面的题需要等待4小时解锁，或者可以通过内购解锁所有关卡。

当然是有破解的方法的，我的经验告诉我，可以通过调系统时间来让软件误以为时间已经过去，测试之后果然有效。

据我所知，这个游戏国内的大部分应用商店都没有，可以在 Google Play 下载，国内的某些论坛/贴吧貌似也有安装包。

另外，这软件到目前（2020年8月1日）为止，是没有汉化的（只有 English 和 Russian）。某些关卡对于别人是数学题，对于我就是英译汉。但其实术语就那么多，那些看不懂的词还可以查自带的术语表（这个真的良心），所以对英语的要求并不高。

立体图形的截面

平面

先上 Wikipedia 对平面的定义

数学上，一个平面（plane）就是基本的二维对象。直观的讲，它可以视为一个平坦的拥有无穷大面积的纸。多数几何、三角学和制图的基本工作都在二维进行，或者说，在平面上进行。

众所周知，三个点可以定义一个平面，两点可以定义一条直线。

那么，四个点定义的两条不平行的直线，并不一定会相交，因为这四个点不一定处在同一个平面上。

所以，尽管不能切换视图，但某些看起来相交却无法作出交点的线时刻提醒着你正处在一个三维的世界中。

平面几何就是在一个平面上展开的。根据长期以来的经验，显然，一个平面上任意个点都是处在同一平面的，可以相交（或平行）。并且，这个平面上任意三个点都可以确定这个平面。

为什么要强调这个呢？因为这个游戏中许多解法的证明都是与这个有关的。

截面

游戏中大部分的问题是和立体图形的截面有关的。下面是 Wikipedia 对截面的定义：

截面（英语：Cross section）为一几何学名词，是指一三维空间下的物体和一平面相交所产生交集。截面的面积称为截面积。

截面，顾名思义，它是一个面。这个面是有限的，也就是说它存在面积。它是一个平面落在物体上的一个部分。

举个栗子：

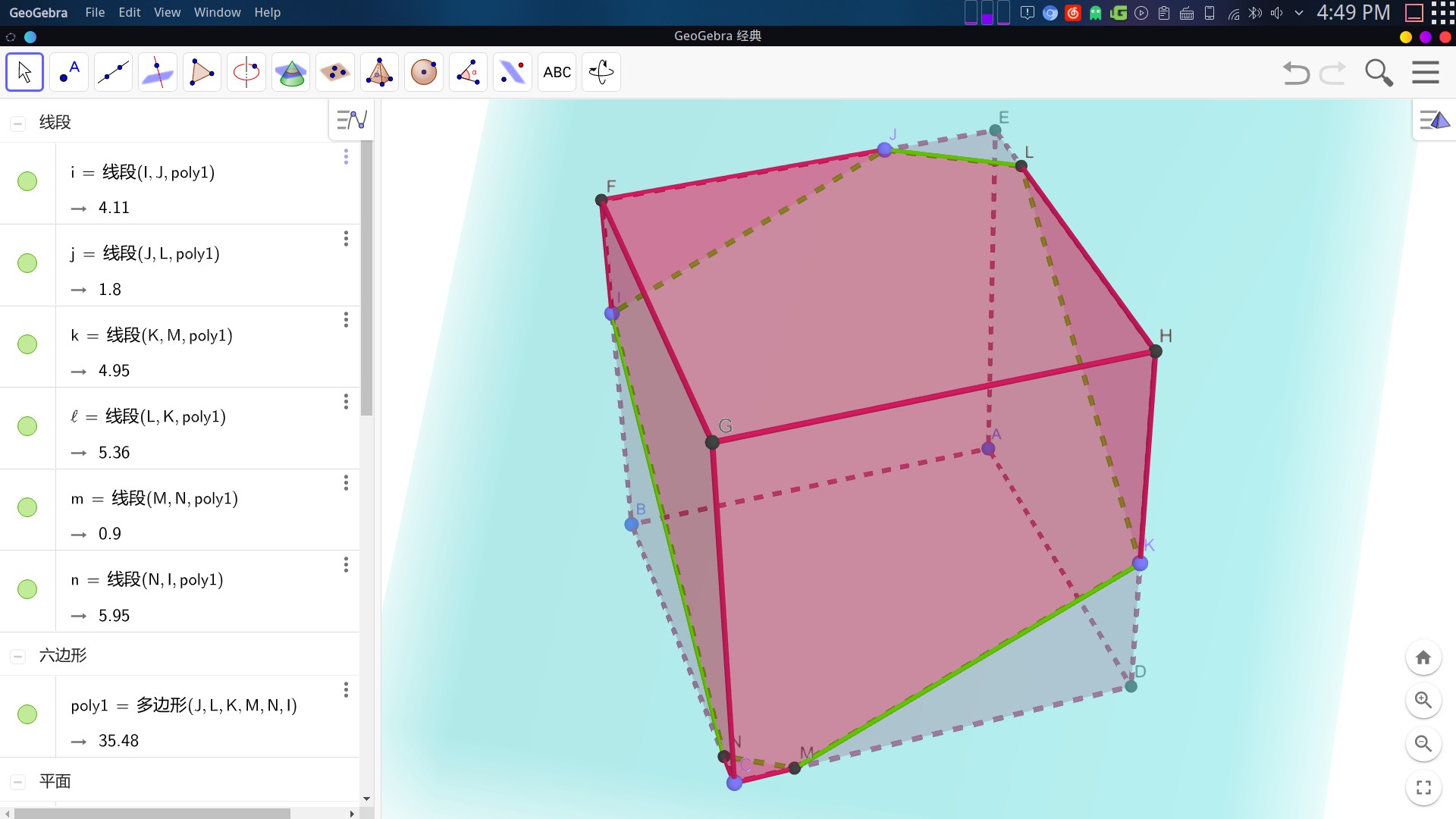
图中的六边形 JLKMNI 就是淡蓝色平面和正方体所产生的截面。可以将它想象成这个蓝色的面将这个正方体切成了两块，截面就是切下去之后多出来的那个面。

插句题外话，这幅图使用 GeoGebra 画出来的，这是一个非常好用的数学软件，之后应该会出一个关于它的介绍。我会把我所有的演示文件放到 我的GeoGebra主页 上了，不需要下载软件，直接在网页里就可以看。

To be continued……