数据结构 之树

树的概念

　　树(tree) 是一种抽象的数据类型（ADT） 获知实作这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由 n n(n>=1) 个有限节点组成一个具有层次关系的集合。把它叫做“树” 是因为它看起来像一棵树，也就是根朝上，而叶朝下的。它具有以下特点：

• 每个节点有0 个或多个子节点
• 没有父节点的节点称为根节点
• 每一个非根节点有且具有一个父节点
• 除了根节点，每个子节点可以分为多个不相交的子树

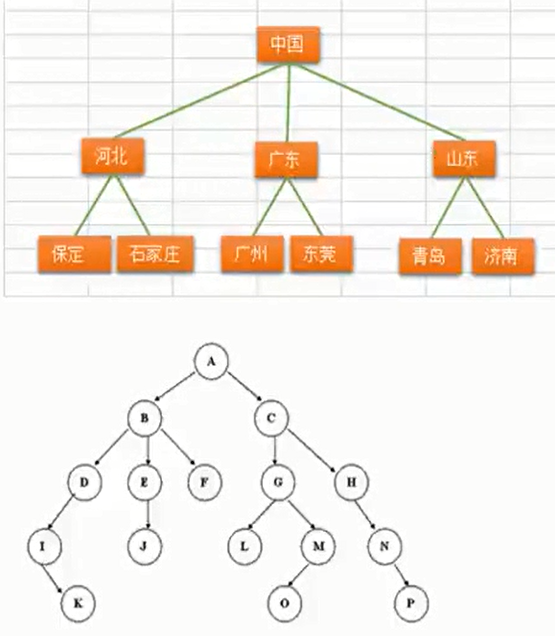
相关术语

节点的度：一个节点含有的子树的个数称为该节点的度；

 

叶节点或终端节点：度为0的节点称为叶节点；

 

非终端节点或分支节点：度不为0的节点；

 

双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；

 

孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；

 

兄弟节点：具有相同父节点的节点互称为兄弟节点；

 

树的度：一棵树中，最大的节点的度称为树的度；

 

节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；

 

树的高度或深度：树中节点的最大层次；

 

堂兄弟节点：双亲在同一层的节点互为堂兄弟；

 

节点的祖先：从根到该节点所经分支上的所有节点；

 

子孙：以某节点为根的子树中任一节点都称为该节点的子孙。

 

森林：由m（m>=0）棵互不相交的树的集合称为森林；

 树的种类

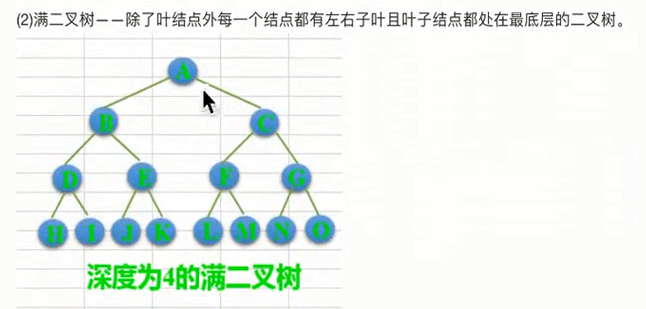
二叉树

　　在计算机科学中，二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。

 

　　一棵深度为k，且有2^k-1个节点的二叉树，称为满二叉树。这种树的特点是每一层上的节点数都是最大节点数。而在一棵二叉树中，除最后一层外，若其余层都是满的，并且最后一层或者是满的，或者是在右边缺少连续若干节点，则此二叉树为完全二叉树。具有n个节点的完全二叉树的深度为floor(log2n)+1。深度为k的完全二叉树，至少有2k-1个叶子节点，至多有2k-1个节点

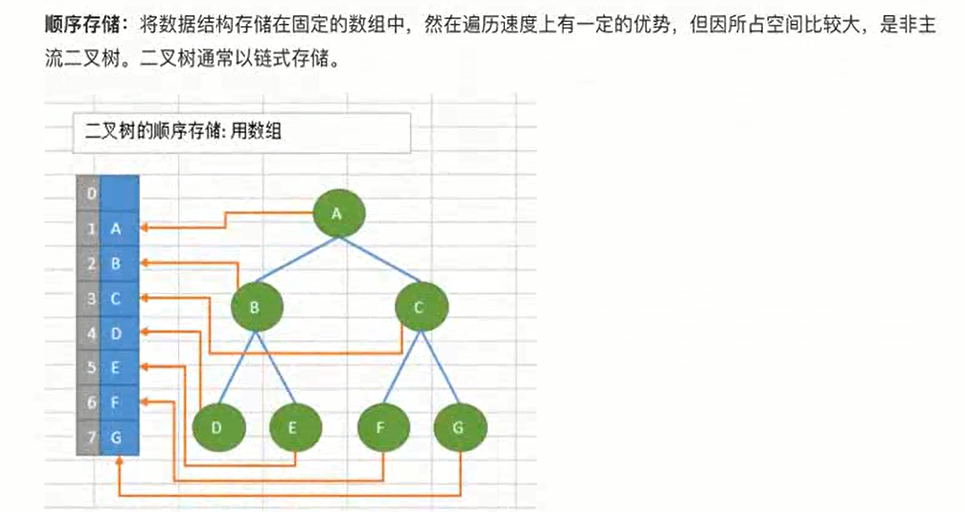
树的存储

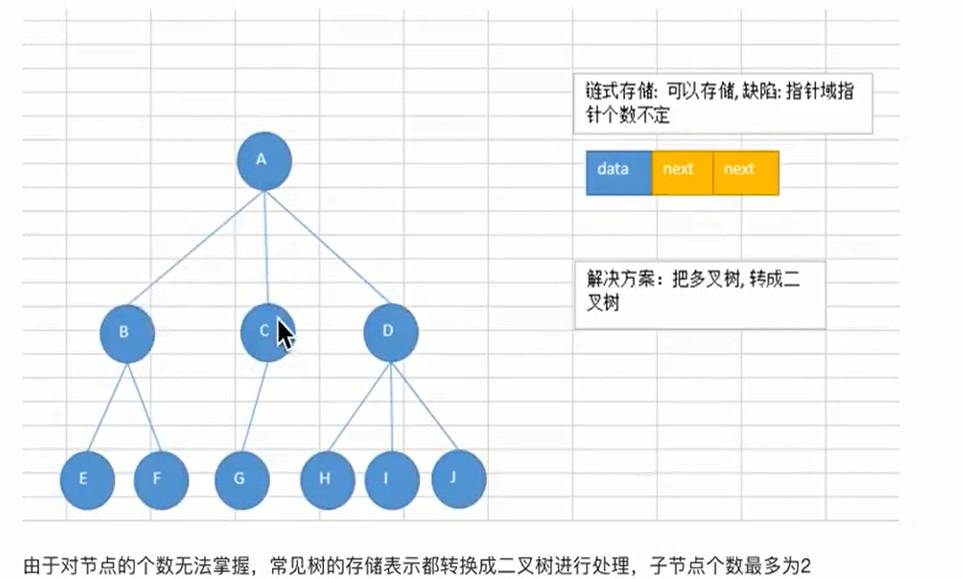
常见使用场景

二叉树创建

class Node(object):
    def __init__(self,item):
        self.elem = item
        self.lchild = None
        self.rchild = None

class Tree(object):
    """二叉树"""
    def __init__(self):
        self.root = None

1. 添加节点：

    def add(self,item):
        node = Node(item)
        if self.root is None:
            self.root = node
            return
        queue = [self.root]
        while queue:
            cur_node = queue.pop(0)
            if cur_node.lchild is None:
                cur_node.lchild = node
                return
            else:
                queue.append(cur_node.lchild)

            if cur_node.rchild is None:
                cur_node.rchild = node
                return
            else:
                queue.append(cur_node.rchild)

2. 广度遍历

    def bread_travel(self):
        """广度遍历"""
        if self.root is None:
            return
        queue = [self.root]
        while queue:
            cur_node = queue.pop(0)
            print(cur_node.elem)
            if cur_node.lchild is not None:
                queue.append(cur_node.lchild)

            if cur_node.rchild is not None:
                queue.append(cur_node.rchild)

3. 前序，中序，后序遍历

    def preorder(self,node):
        if node is None:
            return
        print(node.elem, end='  ')
        self.preorder(node.lchild)
        self.preorder(node.rchild)


    def inorder(self,node):
        if node is None:
            return
        self.inorder(node.lchild)
        print(node.elem, end='  ')
        self.inorder(node.rchild)

    def lastorder(self,node): 
        if node is None:
            return
        self.lastorder(node.lchild)
        self.lastorder(node.rchild)
        print(node.elem,end='  ')

后序： 左子树    - >  右子树  ->   根节点

中序： 左子树    - >  根节点  ->  右子树

前序： 根节点    ->   左子树  ->  右子树