先序遍历
先序遍历规则
先序遍历的核心思想:1.访问根节点;2.访问当前节点的左子树;3.若当前节点无左子树,则访问当前节点的右子树;即考察到一个节点后,即刻输出该节点的值,并继续遍历其左右子树。(根左右)
先序遍历举例
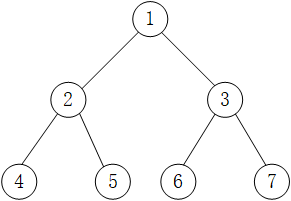
如图所示,采用先序遍历访问这颗二叉树的详细过程为:
1.访问该二叉树的根节点,找到 1;
2.访问节点 1 的左子树,找到节点 2;
3.访问节点 2 的左子树,找到节点 4;
4.由于访问节点 4 左子树失败,且也没有右子树,因此以节点 4 为根节点的子树遍历完成。但节点 2 还没有遍历其右子树,因此现在开始遍历,即访问节点 5;
5.由于节点 5 无左右子树,因此节点 5 遍历完成,并且由此以节点 2 为根节点的子树也遍历完成。现在回到节点 1 ,并开始遍历该节点的右子树,即访问节点 3;
6.访问节点 3 左子树,找到节点 6;
7.由于节点 6 无左右子树,因此节点 6 遍历完成,回到节点 3 并遍历其右子树,找到节点 7;
8.节点 7 无左右子树,因此以节点 3 为根节点的子树遍历完成,同时回归节点 1。由于节点 1 的左右子树全部遍历完成,因此整个二叉树遍历完成;
因此,图 中二叉树采用先序遍历得到的序列为:1 2 4 5 3 6 7
先序遍历代码(递归)
/*
* @Description:
* @Version:
* @Autor: Carlos
* @Date: 2020-05-29 16:55:41
* @LastEditors: Carlos
* @LastEditTime: 2020-05-30 17:03:23
*/
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define TElemType int
//构造结点的结构体
typedef struct BiTNode{
TElemType data;//数据域
struct BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;
/**
* @Description: 初始化树的函数
* @Param: BiTree *T 结构体指针的指针
* @Return: 无
* @Author: Carlos
*/
void CreateBiTree(BiTree *T){
*T=(BiTree)malloc(sizeof(BiTNode));
//根节点
(*T)->data=1;
(*T)->lchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->rchild=(BiTree)malloc(sizeof(BiTNode));
//1节点的左孩子2
(*T)->lchild->data=2;
(*T)->lchild->lchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->lchild->rchild=(BiTree)malloc(sizeof(BiTNode));
//2节点的右孩子5
(*T)->lchild->rchild->data=5;
(*T)->lchild->rchild->lchild=NULL;
(*T)->lchild->rchild->rchild=NULL;
//1节点的右孩子3
(*T)->rchild->data=3;
(*T)->rchild->lchild=(BiTree)malloc(sizeof(BiTNode));
//3节点的左孩子6
(*T)->rchild->lchild->data=6;
(*T)->rchild->lchild->lchild=NULL;
(*T)->rchild->lchild->rchild=NULL;
(*T)->rchild->rchild=(BiTree)malloc(sizeof(BiTNode));
//3节点的右孩子7
(*T)->rchild->rchild->data=7;
(*T)->rchild->rchild->lchild=NULL;
(*T)->rchild->rchild->rchild=NULL;
//2节点的左孩子4
(*T)->lchild->lchild->data=4;
(*T)->lchild->lchild->lchild=NULL;
(*T)->lchild->lchild->rchild=NULL;
}
/**
* @Description: 模拟操作结点元素的函数,输出结点本身的数值
* @Param:BiTree elem 就结构体指针
* @Return: 无
* @Author: Carlos
*/
void PrintBiT(BiTree elem){
printf("%d ",elem->data);
}
/**
* @Description: 先序遍历
* @Param: BiTree T 结构体指针
* @Return: 无
* @Author: Carlos
*/
void PreOrderTraverse(BiTree T){
if (T) {
PrintBiT(T);//调用操作结点数据的函数方法
PreOrderTraverse(T->lchild);//访问该结点的左孩子
PreOrderTraverse(T->rchild);//访问该结点的右孩子
}
//如果结点为空,返回上一层
return;
}
int main() {
BiTree Tree;
CreateBiTree(&Tree);
printf("先序遍历:
");
PreOrderTraverse(Tree);
}
先序遍历代码(非递归)
因为要在遍历完某个树的根节点的左子树后接着遍历节点的右子树,为了能找到该树的根节点,需要使用栈来进行暂存。中序和后序也都涉及到回溯,所以都需要用到栈。
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define TElemType int
//构造结点的结构体
typedef struct BiTNode{
TElemType data;//数据域
struct BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;
int top = -1;
//定义一个顺序栈
BiTree a[20];
/**
* @Description: 初始化树
* @Param: BiTree *T 指针的指针
* @Return: 无
* @Author: Carlos
*/
void CreateBiTree(BiTree *T){
*T=(BiTree)malloc(sizeof(BiTNode));
//根节点
(*T)->data=1;
(*T)->lchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->rchild=(BiTree)malloc(sizeof(BiTNode));
//1节点的左孩子2
(*T)->lchild->data=2;
(*T)->lchild->lchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->lchild->rchild=(BiTree)malloc(sizeof(BiTNode));
//2节点的右孩子5
(*T)->lchild->rchild->data=5;
(*T)->lchild->rchild->lchild=NULL;
(*T)->lchild->rchild->rchild=NULL;
//1节点的右孩子3
(*T)->rchild->data=3;
(*T)->rchild->lchild=(BiTree)malloc(sizeof(BiTNode));
//3节点的左孩子6
(*T)->rchild->lchild->data=6;
(*T)->rchild->lchild->lchild=NULL;
(*T)->rchild->lchild->rchild=NULL;
(*T)->rchild->rchild=(BiTree)malloc(sizeof(BiTNode));
//3节点的右孩子7
(*T)->rchild->rchild->data=7;
(*T)->rchild->rchild->lchild=NULL;
(*T)->rchild->rchild->rchild=NULL;
//2节点的左孩子4
(*T)->lchild->lchild->data=4;
(*T)->lchild->lchild->lchild=NULL;
(*T)->lchild->lchild->rchild=NULL;
}
/**
* @Description: 打印二叉树
* @Param: BiTree elem 指针的指针
* @Return: 无
* @Author: Carlos
*/
void PrintBiT(BiTree elem){
printf("%d ",elem->data);
}
/**
* @Description: 二叉树压栈函数
* @Param: BiTree* a 结构体指针的指针(也可以理解为指针数组) BiTree elem 结构体指针
* @Return: 无
* @Author: Carlos
*/
void Push(BiTree* a,BiTree elem)
{
a[++top]=elem;
}
/**
* @Description: 二叉树弹栈函数
* @Param: 无
* @Return: 无
* @Author: Carlos
*/
void Pop()
{
if (top==-1) {
return ;
}
top--;
}
/**
* @Description: 获取栈顶元素
* @Param: BiTree*a 结构体指针数组
* @Return: 结构体指针
* @Author: Carlos
*/
BiTree GetTop(BiTree*a){
return a[top];
}
/**
* @Description: 先序遍历
* @Param: BiTree Tree 结构体指针
* @Return: 无
* @Author: Carlos
*/
void PreOrderTraverse(BiTree Tree)
{
//临时指针
BiTree p;
//根结点进栈
Push(a, Tree);
while (top!=-1) {
//取栈顶元素
p=GetTop(a);
//弹栈
Pop();
while (p) {
//调用结点的操作函数
PrintBiT(p);
//如果该结点有右孩子,右孩子进栈
if (p->rchild) {
Push(a,p->rchild);
}
p=p->lchild;//一直指向根结点最后一个左孩子
}
}
}
int main() {
BiTree Tree;
CreateBiTree(&Tree);
printf("先序遍历:
");
PreOrderTraverse(Tree);
}
中序遍历
中序遍历规则
二叉树中序遍历的实现思想是:1.访问当前节点的左子树;2.访问根节点;3.访问当前节点的右子树。即考察到一个节点后,将其暂存,遍历完左子树后,再输出该节点的值,然后遍历右子树。(左根右)
中序遍历举例
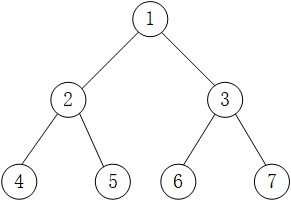
以上图为例,采用中序遍历的思想遍历该二叉树的过程为:
1.访问该二叉树的根节点,找到 1;
2.遍历节点 1 的左子树,找到节点 2;
3.遍历节点 2 的左子树,找到节点 4;
4.由于节点 4 无左孩子,因此找到节点 4,并遍历节点 4 的右子树;
5.由于节点 4 无右子树,因此节点 2 的左子树遍历完成,访问节点 2;
6.遍历节点 2 的右子树,找到节点 5;
7.由于节点 5 无左子树,因此访问节点 5 ,又因为节点 5 没有右子树,因此节点 1 的左子树遍历完成,访问节点 1 ,并遍历节点 1 的右子树,找到节点 3;
8.遍历节点 3 的左子树,找到节点 6;
9.由于节点 6 无左子树,因此访问节点 6,又因为该节点无右子树,因此节点 3 的左子树遍历完成,开始访问节点 3 ,并遍历节点 3 的右子树,找到节点 7;
10.由于节点 7 无左子树,因此访问节点 7,又因为该节点无右子树,因此节点 1 的右子树遍历完成,即整棵树遍历完成;
因此,上图中二叉树采用中序遍历得到的序列为:4 2 5 1 6 3 7
中序遍历代码(递归)
/*
* @Description: 递归实现的中序遍历
* @Version: V1.0
* @Autor: Carlos
* @Date: 2020-05-18 14:53:29
* @LastEditors: Carlos
* @LastEditTime: 2020-05-30 17:21:06
*/
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define TElemType int
//构造结点的结构体
typedef struct BiTNode{
//数据域
TElemType data;
//左右孩子指针
struct BiTreelchild,*rchild;
}BiTNode,*BiTree;
/**
* @Description: 初始化树
* @Param: BiTree *T 结构体指针的指针(指针数组)
* @Return: 无
* @Author: Carlos
*/
void CreateBiTree(BiTree *T){
*T=(BiTree)malloc(sizeof(BiTNode));
(*T)->data=1;
(*T)->lchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->rchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->lchild->data=2;
(*T)->lchild->lchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->lchild->rchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->lchild->rchild->data=5;
(*T)->lchild->rchild->lchild=NULL;
(*T)->lchild->rchild->rchild=NULL;
(*T)->rchild->data=3;
(*T)->rchild->lchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->rchild->lchild->data=6;
(*T)->rchild->lchild->lchild=NULL;
(*T)->rchild->lchild->rchild=NULL;
(*T)->rchild->rchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->rchild->rchild->data=7;
(*T)->rchild->rchild->lchild=NULL;
(*T)->rchild->rchild->rchild=NULL;
(*T)->lchild->lchild->data=4;
(*T)->lchild->lchild->lchild=NULL;
(*T)->lchild->lchild->rchild=NULL;
}
/**
* @Description: 显示函数
* @Param: BiTree elem 结构体指针
* @Return: 无
* @Author: Carlos
*/
void PrintBiT(BiTree elem){
printf("%d ",elem->data);
}
/**
* @Description: 中序遍历
* @Param: BiTree T 结构体指针
* @Return: 无
* @Author: Carlos
*/
void INOrderTraverse(BiTree T){
if (T) {
INOrderTraverse(T->lchild);//遍历左孩子
PrintBiT(T);//调用操作结点数据的函数方法
INOrderTraverse(T->rchild);//遍历右孩子
}
//如果结点为空,返回上一层
return;
}
int main() {
BiTree Tree;
CreateBiTree(&Tree);
printf("中序遍历算法:
");
INOrderTraverse(Tree);
}
中序遍历代码(非递归)
和非递归先序遍历类似,唯一区别是考查到当前节点时,并不直接输出该节点。而是当考查节点为空时,从栈中弹出的时候再进行输出(永远先考虑左子树,直到左子树为空才访问根节点)。
/*
* @Description: 二叉树的先序遍历(非递归)
* @Version: V1.0
* @Autor: Carlos
* @Date: 2020-05-17 16:35:27
* @LastEditors: Carlos
* @LastEditTime: 2020-05-18 14:51:01
*/
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define DBG_PRINTF(fmt, args...)
do
{
printf("<<File:%s Line:%d Function:%s>> ", __FILE__, __LINE__, __FUNCTION__);
printf(fmt, ##args);
}while(0)
#define TElemType int
int top=-1;//top变量时刻表示栈顶元素所在位置
//构造结点的结构体
typedef struct BiTNode{
//数据域
TElemType data;
//左右孩子指针
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
/**
* @Description: 初始化树
* @Param: BiTree *T 结构体指针的指针
* @Return: 无
* @Author: Carlos
*/
void CreateBiTree(BiTree *T){
*T=(BiTree)malloc(sizeof(BiTNode));
(*T)->data=1;
(*T)->lchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->rchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->lchild->data=2;
(*T)->lchild->lchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->lchild->rchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->lchild->rchild->data=5;
(*T)->lchild->rchild->lchild=NULL;
(*T)->lchild->rchild->rchild=NULL;
(*T)->rchild->data=3;
(*T)->rchild->lchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->rchild->lchild->data=6;
(*T)->rchild->lchild->lchild=NULL;
(*T)->rchild->lchild->rchild=NULL;
(*T)->rchild->rchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->rchild->rchild->data=7;
(*T)->rchild->rchild->lchild=NULL;
(*T)->rchild->rchild->rchild=NULL;
(*T)->lchild->lchild->data=4;
(*T)->lchild->lchild->lchild=NULL;
(*T)->lchild->lchild->rchild=NULL;
}
/**
* @Description: 中序遍历使用的进栈函数
* @Param: BiTree* a 指向树的指针数组 BiTree elem 进栈的元素
* @Return: 无
* @Author: Carlos
*/
void Push(BiTree* a,BiTree elem){
//指针进栈
a[++top]=elem;
}
/**
* @Description: 前序遍历使用的弹栈函数
* @Param: 无
* @Return: 无
* @Author: Carlos
*/
void Pop( ){
if (top==-1) {
return;
}
top--;
}
/**
* @Description: 显示函数
* @Param: BiTree elem 指向树的指针
* @Return: 无
* @Author: Carlos
*/
void PrintBiT(BiTree elem){
printf("%d ",elem->data);
}
/**
* @Description: 拿到栈顶元素
* @Param: BiTree*a 指针数组
* @Return: 栈顶元素的地址
* @Author: Carlos
*/
BiTree GetTop(BiTree*a){
return a[top];
}
/**
* @Description: 中序遍历非递归算法,先左,然后回退,然后右。从根结点开始,遍历左孩子同时压栈,当遍历结束,说明当前遍历的结点没有左孩子,
* 从栈中取出来调用操作函数,然后访问该结点的右孩子,继续以上重复性的操作
* @Return: 栈顶元素的地址
* @Author: Carlos
*/
void InOrderTraverse1(BiTree Tree){
//定义一个顺序栈
BiTree a[20];
//临时指针
BiTree p;
//根结点进栈
Push(a, Tree);
//top!=-1说明栈内不为空,程序继续运行
while (top!=-1) {
//一直取栈顶元素,且不能为NULL
while ((p=GetTop(a)) &&p){
//将该结点的左孩子进栈,如果没有左孩子,NULL进栈
Push(a, p->lchild);
}
//跳出循环,栈顶元素肯定为NULL,将NULL弹栈。 打印的第一个元素没有右孩子,所以也会Pop掉,再取栈顶元素就是第一个元素的父节点
Pop();
if (top!=-1) {
//取栈顶元素
p=GetTop(a);
//栈顶元素弹栈
Pop();
//遍历完所有左孩子之后,打印栈顶的元素。
PrintBiT(p);
//将p指向的结点的右孩子进栈
Push(a, p->rchild);
}
}
}
/**
* @Description: 中序遍历非递归算法。中序遍历过程中,只需将每个结点的左子树压栈即可,右子树不需要压栈。
* 当结点的左子树遍历完成后,只需要以栈顶结点的右孩子为根结点,继续循环遍历即可
* @Param: 无
* @Return: 栈顶元素的地址
* @Author: Carlos
*/
void InOrderTraverse2(BiTree Tree){
//定义一个顺序栈
BiTree a[20];
//临时指针
BiTree p;
p=Tree;
//当p为NULL或者栈为空时,表明树遍历完成
while (p || top!=-1) {
//如果p不为NULL,将其压栈并遍历其左子树
if (p) {
Push(a, p);
p=p->lchild;
}
//如果p==NULL,表明左子树遍历完成,需要遍历上一层结点的右子树 弹出时顺便访问右子树
else{
p=GetTop(a);
Pop();
PrintBiT(p);
p=p->rchild;
}
}
}
int main(){
BiTree Tree;
CreateBiTree(&Tree);
printf("中序遍历:
");
InOrderTraverse2(Tree);
DBG_PRINTF("123456
");
return 0;
}
后序遍历
后序遍历规则
二叉树后序遍历的实现思想是:1.访问左子树;2.访问右子树;3.完成该节点的左右子树的访问后,再访问该节点。即考察到一个节点后,将其暂存,遍历完左右子树后,再输出该节点的值。(左右根)
后序遍历举例
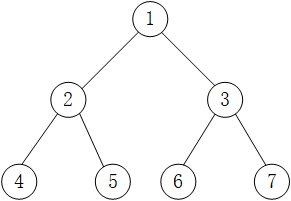
如上图中,对此二叉树进行后序遍历的操作过程为:
从根节点 1 开始,遍历该节点的左子树(以节点 2 为根节点);
1.遍历节点 2 的左子树(以节点 4 为根节点);
2.由于节点 4 既没有左子树,也没有右子树,此时访问该节点中的元素 4,并回退到节点 2 ,遍历节点 2 的右子树(以 5 为根节点);
3.由于节点 5 无左右子树,因此可以访问节点 5 ,并且此时节点 2 的左右子树也遍历完成,因此也可以访问节点 2;
4.此时回退到节点 1 ,开始遍历节点 1 的右子树(以节点 3 为根节点);
5.遍历节点 3 的左子树(以节点 6 为根节点);
6.由于节点 6 无左右子树,因此访问节点 6,并回退到节点 3,开始遍历节点 3 的右子树(以节点 7 为根节点);
7.由于节点 7 无左右子树,因此访问节点 7,并且节点 3 的左右子树也遍历完成,可以访问节点 3;节点 1 的左右子树也遍历完成,可以访问节点 1;
由此,对上图 中二叉树进行后序遍历的结果为:4 5 2 6 7 3 1
后序遍历代码(递归)
/*
* @Description: 二叉树的后序遍历(递归)
* @Version: V1.0
* @Autor: Carlos
* @Date: 2020-05-18 16:23:57
* @LastEditors: Carlos
* @LastEditTime: 2020-05-30 17:29:38
*/
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define TElemType int
//构造结点的结构体
typedef struct BiTNode{
//数据域
TElemType data;
//左右孩子指针
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
/**
* @Description: 初始化树
* @Param: BiTree *T 结构体指针
* @Return: 无
* @Author: Carlos
*/
void CreateBiTree(BiTree *T){
*T=(BiTree)malloc(sizeof(BiTNode));
(*T)->data=1;
(*T)->lchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->rchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->lchild->data=2;
(*T)->lchild->lchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->lchild->rchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->lchild->rchild->data=5;
(*T)->lchild->rchild->lchild=NULL;
(*T)->lchild->rchild->rchild=NULL;
(*T)->rchild->data=3;
(*T)->rchild->lchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->rchild->lchild->data=6;
(*T)->rchild->lchild->lchild=NULL;
(*T)->rchild->lchild->rchild=NULL;
(*T)->rchild->rchild=(BiTree)malloc(sizeof(BiTNode));
(*T)->rchild->rchild->data=7;
(*T)->rchild->rchild->lchild=NULL;
(*T)->rchild->rchild->rchild=NULL;
(*T)->lchild->lchild->data=4;
(*T)->lchild->lchild->lchild=NULL;
(*T)->lchild->lchild->rchild=NULL;
}
/**
* @Description: 显示函数
* @Param: BiTree elem 指向树的结构体指针
* @Return: 无
* @Author: Carlos
*/
void PrintBiT(BiTree elem){
printf("%d ",elem->data);
}
/**
* @Description: 先序遍历
* @Param: BiTree T 指针数组,存放各个节点的指针
* @Return: 无
* @Author: Carlos
*/
void PreOrderTraverse(BiTree T){
if (T) {
PreOrderTraverse(T->lchild);//访问该结点的左孩子
PreOrderTraverse(T->rchild);//访问该结点的右孩子
PrintBiT(T);//调用操作结点数据的函数方法
}
//如果结点为空,返回上一层
return;
}
int main() {
BiTree Tree;
CreateBiTree(&Tree);
printf("后序遍历:
");
PreOrderTraverse(Tree);
}
后序遍历代码(非递归)
/*
* @Description: 二叉树的后序遍历(非递归)
* @Version: V1.0
* @Autor: Carlos
* @Date: 2020-05-18 16:23:57
* @LastEditors: Carlos
* @LastEditTime: 2020-05-18 16:24:29
*/
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define TElemType int
//top变量时刻表示栈顶元素所在位置
int top=-1;
//构造结点的结构体
typedef struct BiTNode{
//数据域
TElemType data;
//左右孩子指针
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
/**
* @Description: 初始化树
* @Param: BiTree *T 结构体指针数组
* @Return: 无
* @Author: Carlos
*/
void CreateBiTree(BiTree *T){
*T=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->data=1;
(*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->data=2;
(*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->rchild->data=5;
(*T)->lchild->rchild->lchild=NULL;
(*T)->lchild->rchild->rchild=NULL;
(*T)->rchild->data=3;
(*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild->lchild->data=6;
(*T)->rchild->lchild->lchild=NULL;
(*T)->rchild->lchild->rchild=NULL;
(*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild->rchild->data=7;
(*T)->rchild->rchild->lchild=NULL;
(*T)->rchild->rchild->rchild=NULL;
(*T)->lchild->lchild->data=4;
(*T)->lchild->lchild->lchild=NULL;
(*T)->lchild->lchild->rchild=NULL;
}
/**
* @Description: 后序遍历使用的弹栈函数
* @Param: 无
* @Return: 无
* @Author: Carlos
*/
void Pop( ){
if (top==-1) {
return ;
}
top--;
}
/**
* @Description: 显示函数
* @Param: 无
* @Return: 无
* @Author: Carlos
*/
void PrintBiT(BiTree elem){
printf("%d ",elem->data);
}
//增加左右子树的访问标志
typedef struct SNode{
BiTree p;
int tag;
}SNode;
/**
* @Description: 后序遍历使用的进栈函数
* @Param: SNode *a 指向树和标志位的结构体的指针 BiTree sdata 进栈的元素
* @Return: 无
* @Author: Carlos
*/
void Push(SNode *a,SNode sdata){
a[++top]=sdata;
}
/**
* @Description: 后序遍历非递归算法。后序遍历是在遍历完当前结点的左右孩子之后,才调用操作函数,所以需要在操作结点进栈时,为每个结点配备一个标志位。
* 当遍历该结点的左孩子时,设置当前结点的标志位为 0,进栈;当要遍历该结点的右孩子时,设置当前结点的标志位为 1,进栈。这样,当遍历完成,该结点弹栈时,
* 查看该结点的标志位的值:如果是 0,表示该结点的右孩子还没有遍历;反之如果是 1,说明该结点的左右孩子都遍历完成,可以调用操作函数。
* @Param: 结构体指针数组
* @Return: 无
* @Author: Carlos
*/
void PostOrderTraverse(BiTree Tree){
//定义一个顺序栈
SNode a[20];
//临时指针
BiTree p;
int tag;
SNode sdata;
p=Tree;
while (p||top!=-1) {
//左孩子进栈
while (p) {
//为该结点入栈做准备
sdata.p=p;
//由于遍历是左孩子,设置标志位为0
sdata.tag=0;
//压栈
Push(a, sdata);
//以该结点为根结点,遍历左孩子
p=p->lchild;
}
//取栈顶元素 取左孩子的父节点
sdata=a[top];
//栈顶元素弹栈
Pop();
p=sdata.p;
tag=sdata.tag;
//右孩子进栈
//如果tag==0,说明该结点还没有遍历它的右孩子
if (tag==0) {
sdata.p=p;
sdata.tag=1;
//更改该结点的标志位,重新压栈
Push(a, sdata);
//以该结点的右孩子为根结点,重复循环
p=p->rchild;
}
//如果取出来的栈顶元素的tag==1,说明此结点左右子树都遍历完了,可以调用操作函数了
else{
PrintBiT(p);
p=NULL;
}
}
}
int main(){
BiTree Tree;
CreateBiTree(&Tree);
printf("后序遍历:
");
PostOrderTraverse(Tree);
}
层次遍历
层次遍历规则
按照二叉树中的层次从左到右依次遍历每层中的结点。通过使用队列的数据结构,从树的根结点开始,依次将其左孩子和右孩子入队。而后每次队列中一个结点出队,都将其左孩子和右孩子入队,直到树中所有结点都出队,出队结点的先后顺序就是层次遍历的最终结果。
层次遍历举例
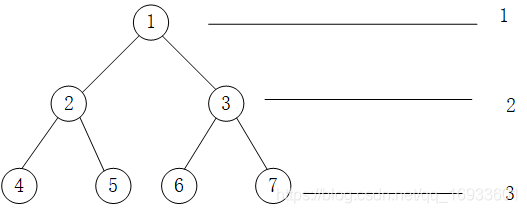
例如,层次遍历如上图中的二叉树:
1.根结点 1 入队;
2.根结点 1 出队,出队的同时,将左孩子 2 和右孩子 3 分别入队;
3.队头结点 2 出队,出队的同时,将结点 2 的左孩子 4 和右孩子 5 依次入队;
4.队头结点 3 出队,出队的同时,将结点 3 的左孩子 6 和右孩子 7 依次入队;
5.不断地循环,直至队列内为空。
层次遍历代码
/*
* @Description: 二叉树的层次遍历
* @Version: V1.0
* @Autor: Carlos
* @Date: 2020-05-20 14:52:38
* @LastEditors: Carlos
* @LastEditTime: 2020-05-30 17:41:48
*/
#include <stdio.h>
#include <stdlib.h>
#define TElemType int
//初始化队头和队尾指针开始时都为0
int front=0,rear=0;
typedef struct BiTNode{
//数据域
TElemType data;
//左右孩子指针
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
//采用顺序队列,初始化创建队列数组
BiTree a[20];
/**
* @Description: 初始化二叉树
* @Param: BiTree *T 二叉树的结构体指针数组
* @Return: 无
* @Author: Carlos
*/
void CreateBiTree(BiTree *T){
*T=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->data=1;
(*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->data=2;
(*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->rchild->data=5;
(*T)->lchild->rchild->lchild=NULL;
(*T)->lchild->rchild->rchild=NULL;
(*T)->rchild->data=3;
(*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild->lchild->data=6;
(*T)->rchild->lchild->lchild=NULL;
(*T)->rchild->lchild->rchild=NULL;
(*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild->rchild->data=7;
(*T)->rchild->rchild->lchild=NULL;
(*T)->rchild->rchild->rchild=NULL;
(*T)->lchild->lchild->data=4;
(*T)->lchild->lchild->lchild=NULL;
(*T)->lchild->lchild->rchild=NULL;
}
/**
* @Description: 入队
* @Param: BiTree *a 二叉树结构体指针 BiTree node 入队的节点
* @Return: 无
* @Author: Carlos
*/
void EnQueue(BiTree *a,BiTree node){
a[rear++]=node;
}
/**
* @Description: 出队
* @Param: BiTree *node 二叉树结构体指针数组
* @Return: 结构体指针
* @Author: Carlos
*/
BiTree DeQueue(BiTree *node){
return a[front++];
}
/**
* @Description: 二叉树输出函数
* @Param: BiTree node 输出的节点
* @Return: 无
* @Author: Carlos
*/
void displayNode(BiTree node){
printf("%d ",node->data);
}
int main() {
BiTree tree;
//初始化二叉树
CreateBiTree(&tree);
BiTree p;
//根结点入队
EnQueue(a, tree);
//当队头和队尾相等时,表示队列为空
while(front<rear) {
//队头结点出队
p=DeQueue(a);
displayNode(p);
//将队头结点的左右孩子依次入队
if (p->lchild!=NULL) {
EnQueue(a, p->lchild);
}
if (p->rchild!=NULL) {
EnQueue(a, p->rchild);
}
}
return 0;
}
总结:其实不管是哪种遍历方式,我们最终的目的就是访问所有的树(子树)的根节点,左孩子,右孩子。那么在访问的过程中,肯定不能一次访问并打印完毕。这个时候就需要栈来暂存我们已经访问过的元素。在需要的时候将其打印出来即可(我们以左孩子节点为基准,先序遍历是在访问左孩子节点之前打印节点,中序遍历是在左孩子节点压栈之后打印节点,后序遍历是在访问完左右孩子节点之后打印节点)。
文中代码均已测试,有任何意见或者建议均可联系我。欢迎学习交流!
如果觉得写的不错,请点个赞再走,谢谢!
有任何问题,均可通过公告中的二维码联系我