题意
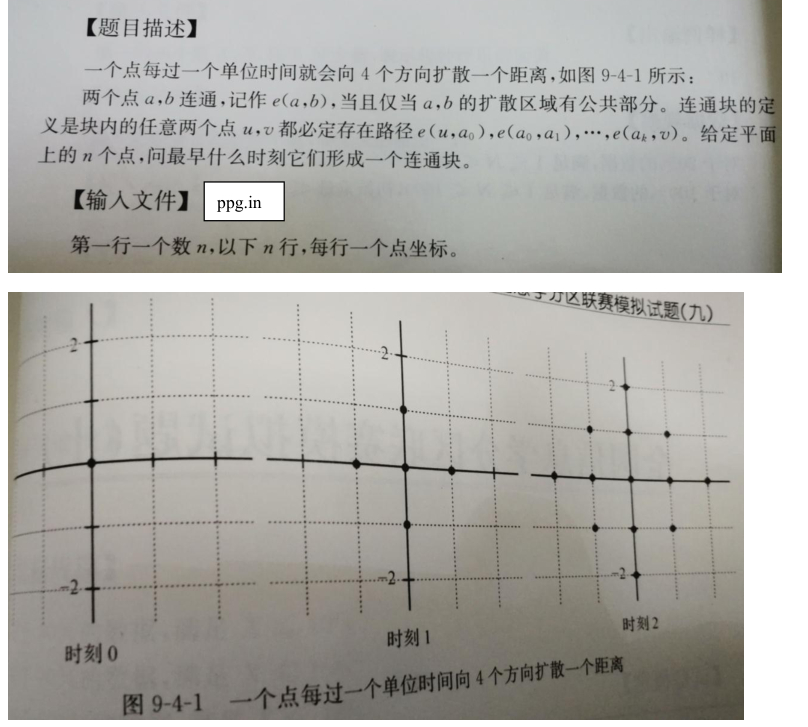
先讲一下一种容易陷入误区错误思路
要使时间最小,就去找相对于每个点的最短曼哈顿距离,然后取最大值,时间就是(maxn+1)/2。
代码
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cstdio>
#include<iostream>
#define ll long long
#define MX 55
using namespace std;
int d[MX][MX];
int x[MX],y[MX];
int ans=0;
int man=1<<30;
int n;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d %d",&x[i],&y[i]);
}
for(int i=1;i<=n;++i){
for(int j=i+1;j<=n;++j){
d[i][j]=d[j][i]=(abs(x[i]-x[j])+abs(y[i]-y[j]));
}
}
for(int i=1;i<=n;++i){
man=1<<30;
for(int j=1;j<=n;++j){
if(i==j) continue;
man=min(d[i][j],man);
}
ans=max(ans,man);
}
printf("%d",(ans+1)/2);
return 0;
}
这样做只有20分,为什么错了?
因为每次取最小的会使你遗漏边,有些边是一定要选的却没选,不选的话会导致联通块不连通,举个例子吧
咕咕,因为图床问题暂时咕咕
如果按照上面的方法就只会选到红边,但黑边至少要选一条,这就会导致联通块不连通,所以错误了。
正解
一种比较巧妙的方法,可以看作在最长距离中找一个最短的曼哈顿距离便可以二分,判断联通可以用并查集或者bfs。
代码
#include<bits/stdc++.h>
using namespace std;
int n,ans,l,r,cnt,fa[60],zx[60],zy[60];
int find(int x){
if(x==fa[x]) return x;
else return fa[x]=find(fa[x]);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d %d",&zx[i],&zy[i]);
}
l=0,r=1e9;
while(l<=r){
int mid=(l+r)>>1;
for(int i=1;i<=n;++i){
fa[i]=i;
}
for(int i=1;i<=n;++i){
for(int j=i+1;j<=n;++j){
int dis=abs(zx[i]-zx[j])+abs(zy[i]-zy[j]);
if(dis<=mid*2){
int fa1=find(i);
int fa2=find(j);
if(fa1!=fa2) fa[fa1]=fa2;
}
}
}
cnt=0;
for(int i=1;i<=n;++i){
if(fa[i]==i) cnt++;
}
if(cnt==1) r=mid-1;
else l=mid+1;
}
printf("%d",l);
return 0;
}
另外这道题还可以计算出任意两点间联通的时间,然后求最小生成树(MST),则MST的最大边就是答案。因为MST的性质之一就是满足任意两点间的最大边权最小。