通过支持向量机(上)和支持向量机(中)的介绍,对支持向量机应该有点感性的认识啦!在这个学习笔记中,来继续探寻带核函数的支持向量机(解决如下图所示的问题)
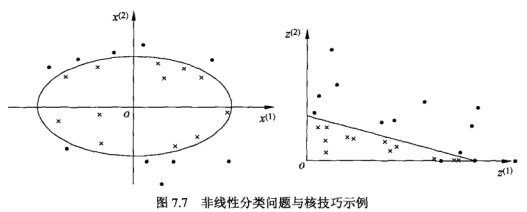
对解线性分类问题,线性分类支持向量机是一种非常有效的方法。但是,有时分类问题是非线性的,这时可以使用非线性支持向量机。
核技巧:
如上图所示,设原空间为$mathcal{X} subset R^2, x = (x^{(1)},x^{(2)})^T in mathcal{X}$,新空间为$mathcal{Z} subset R^2, z = (z^{(1)},z^{(2)})^T in mathcal{Z}$,定义从原空间到新空间的变换(映射):
$$z = phi (x) = ((x^{(1)})^2,(x^{(2)})^2)^T$$
经过变换$z=phi (x)$,原空间$ mathcal{X} subset R^2 $变换为新空间$ mathcal{Z} subset R^2$,原空间中的点相应地变换为新空间中的点,原空间中的椭圆:
$$w_{1}(x^{(1)})^2 +w_{2}(x^{(2)})^2 + b = 0$$
变换成为新空间中的直线:
$$w_{1}z^{(1)} + w_{2}z^{(2)} + b = 0 $$
在变换后的新空间里,直线$w_{1}z^{(1)} + w_{2}z^{(2)} + b = 0$可以将变换后的正负实例点正确分开。这样,原空间的非线性可分问题就变成了新空间的线性可分问题。
上面的例子说明,用线性分类方法求解非线性分类问题分为两步:首先使用一个变换将原空间的数据映射到新空间;然后在新空间里用线性分类学习方法从训练数据中学习分类模型。核技巧就属于这样的方法。
核技巧应用到支持向量机,其基本想法就是通过一个非线性变换将输入空间对应一个特征空间,使得在输入空间$R^n$中的超曲面模型对应于特征空间$mathcal{H}$中的超平面模型(支持向量机)。这样,分类问题的学习任务通过在特征空间中求解线性支持向量机就可以完成。
核函数的定义:
设$mathcal{X}$是输入空间(欧式空间$R^n$的子集或离散集合),又设$mathcal{H}$为特征空间(希尔伯特空间),如果存在一个从$mathcal{X}$到$mathcal{H}$的映射:
$$phi (x): mathcal{X} ightarrow mathcal{H}$$
使得对所有$x,z in mathcal{X}$,函数$K(x,z)$满足条件:
$$K(x,z) = phi (x)cdot phi (z)$$
则称$K(x,z)$为核函数,$phi (x)$为映射函数,式中$phi (x)cdot phi (z) $为$phi (x)$和$phi (z)$的内积。
核技巧的想法是,在学习与预测中只定义核函数$K(x,z)$,而不显示地定义映射函数$phi$。通常,直接计算$K(x,z)$比较容易,而通过$phi (x)$和$phi (z)$计算$K(x,z)$并不容易。注意,$phi$是输入空间$R^n$到特征空间$mathcal{H}$的映射,特征空间$mathcal{H}$一般是高维的,甚至是无穷维的。
核技巧在支持向量机中的应用:
在线性支持向量机的对偶问题中,无论是目标函数还是决策函数(分离超平面)都只涉及输入实例与实例之间的内积。在对偶问题的目标函数中内积$x_icdot x_j$可以用核函数$K(x_i,x_j) = phi (x_i) cdot phi (x_j)$ 来代替。此时对偶问题:
$$W(alpha) = frac{1}{2}sum_{i=1}^{N}sum_{j=1}^{N}alpha_ialpha_jy_iy_jK(x_i,x_j) - sum_{i=1}^{N}alpha_i$$
同样,分类决策函数中的内积也可以用核函数代替,而分类决策函数式为:
$$f(x) = sign(sum_{i=1}^{N_s}alpha_{i}^{*}y_iphi (x_i)cdot phi (x) + b^{*}) = sign(sum_{i=1}^{N_s}alpha_{i}^{*}y_iK(x_i,x) + b^{*})$$
这等价于经过映射函数$phi$将原来的输入空间变换到一个新的特征空间,将输入空间中的内积$x_icdot x_j$变换为特征空间中的内积$phi (x_i)cdot phi (x_j)$,在新的特征空间里从训练样本中学习线性支持向量机。当映射函数是非线性函数时,学习到的含有核函数的支持向量机是非线性分类模型。
也就是说,在核函数$K(x,z)$给定的条件下,可以利用线性分类问题的方法求解非线性分类问题的支持向量机。学习是隐式地在特征空间进行的,不需要显示地定义特征空间和映射函数。这样的技巧称为核技巧,它是巧妙地利用线性分类学习方法与核函数解决非线性问题的技术。在实际应用中,往往依赖领域知识直接选择核函数。下面介绍两种核函数:
常用核函数:
(1)多项式核函数(polynomial kernel function):
$$K(x,z) = (xcdot z + 1)^p$$
对应的支持向量机是一个$p$次多项式分类器。在此情形下,分类决策函数成为:
$$f(x) = sign(sum_{i=1}^{N_s}alpha_{i}^{*}y_i(x_icdot x + 1)^p + b^{*})$$
(2)高斯核函数(Gaussian kernel function)
$$K(x,z) = exp(- frac{||x-z||^2{2sigma^{2}}})$$
对应的支持向量机是高斯径向基函数(radial basis function)分类器。在此情形下,分类决策函数成为:
$$f(x) = sign(sum_{i=1}^{N_s}alpha_{i}^{*}y_iexp(- frac{||x-z||^2}{2sigma^{2}}) + b^*)$$
非线性支持向量机学习算法:
输入:训练数据集$T = {(x_1,y_1),(x_2,y_2),...,(x_N,y_N)}$,其中$x_i in mathcal{X} = R^n, y_i in mathcal{Y} = {-1,+1},i=1,2,...,N$;
输出:分类决策函数
(1)选取适当的核函数$K(x,z)$和适当的参数$C$,构造并求解最优化问题:
$$min_{alpha} frac{1}{2}sum_{i=1}^{N}sum_{j=1}^{N}alpha_ialpha_jy_iy_jK(x_i,x_j) - sum_{i=1}^{N}alpha_i$$
$$s.t. sum_{i=1}^{N}alpha_iy_i = 0$$
$$ 0 leq alpha_i leq C, i=1,2,...,N$$
求得最优解$alpha^{*} = (alpha_{1}^{*},alpha_{2}^{*},...,alpha_{N}^{*})^T$
(2)选择$alpha^{*}$的一个正分量$0<alpha_{j}^{*}<C$,计算
$$b^{*} = y_j - sum_{i=1}^{N}alpha_{i}^{*}y_iK(x_icdot x_j)$$
(3)构造决策函数:
$$f(x) = sign(sum_{i=1}^{N}alpha_{i}^{*}y_iK(xcdot x_i) + b^{*})$$
当$K(x,z)$是正定核函数时,上述目标函数是凸二次规划问题,解是存在的。对偶算法的实现请参考序列最小最优化算法。