深度学习与Pytorch入门实战（十四）时间序列预测

笔记摘抄

1. 问题描述

• 已知 [k, k+n)时刻的正弦函数，预测 [k+t, k+n+t)时刻的正弦曲线。

• 因为每个时刻曲线上的点是一个值，即feature_len=1

• 如果给出50个时刻的点，即seq_len=50

• 如果只提供一条曲线供输入，即batch=1

• 输入的shape=[seq_len, batch, feature_len] = [50, 1, 1]。

2. 代码实现

import torch
import torch.nn as nn
import numpy as np
import torch.optim as optim
from matplotlib import pyplot as plt 

input_size = 1
batch_size = 1
hidden_size = 16
num_layers = 1
output_size = 1

class Net(nn.Module):

    def __init__(self):
        super().__init__()

        self.rnn = nn.RNN(
            input_size=input_size,       # feature_len = 1
            hidden_size=hidden_size,     # 隐藏记忆单元个数hidden_len = 16
            num_layers=num_layers,       # 网络层数 = 1
            batch_first=True             # 在传入数据时,按照[batch,seq_len,feature_len]的格式
        )

        for p in self.rnn.parameters():  # 对RNN层的参数做初始化
            nn.init.normal_(p, mean=0.0, std=0.001)

        self.linear = nn.Linear(hidden_size, output_size) # 输出层

    def forward(self, x, hidden_prev):
        """
        x：一次性输入所有样本所有时刻的值(batch,seq_len,feature_len)
        hidden_prev：第一个时刻空间上所有层的记忆单元(batch, num_layer, hidden_len)
        输出out(batch,seq_len,hidden_len) 和 hidden_prev(batch,num_layer,hidden_len)
        """
        out, hidden_prev = self.rnn(x, hidden_prev)
       
        # 因为要把输出传给线性层处理，这里将batch和seq_len维度打平
        # 再把batch=1添加到最前面的维度（为了和y做MSE）
        # [batch=1,seq_len,hidden_len]->[seq_len,hidden_len]
        out = out.view(-1, hidden_size)  
        #[seq_len,hidden_len]->[seq_len,output_size=1]
        out = self.linear(out)
        
        # [seq_len,output_size=1]->[batch=1,seq_len,output_size=1]
        out = out.unsqueeze(dim=0)

        return out, hidden_prev

# 训练过程
learning_rate = 0.01

model = Net()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=learning_rate)

hidden_prev = torch.zeros(batch_size, num_layers, hidden_size)      #  初始化记忆单元h0[batch,num_layer,hidden_len]

num_time_steps = 50    # 区间内取多少样本点


for iter in range(6000):
    start = np.random.randint(3, size=1)[0]                      # 在0~3之间随机取开始的时刻点
    time_steps = np.linspace(start, start + 10, num_time_steps)   # 在[start,start+10]区间均匀地取num_points个点
    data = np.sin(time_steps)
    data = data.reshape(num_time_step, 1)                        # [num_time_steps,] -> [num_points,1]
    # 输入前49个点(seq_len=49)，即下标0~48 [batch, seq_len, feature_len]
    x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
    # 预测后49个点，即下标1~49
    y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)     
    # 以上步骤生成(x,y)数据对

    output, hidden_prev = model(x, hidden_prev)   # 喂入模型得到输出
    hidden_prev = hidden_prev.detach()            # at

    loss = criterion(output, y)                   # 计算MSE损失   
    model.zero_grad()
    loss.backward()
    optimizer.step()

    if iter % 1000 == 0:
        print("Iteration: {} loss {}".format(iter, loss.item()))

    
# 测试过程
# 先用同样的方式生成一组数据x,y
start = np.random.randint(3, size=1)[0]
time_steps = np.linspace(start, start + 10, num_time_steps)
data = np.sin(time_steps)
data = data.reshape(num_time_steps, 1)
x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)

predictions = []

input = x[:, 0, :]                      # 取seq_len里面第0号数据
input = input.view(1, 1, 1)             # input：[1,1,1]
for _ in range(x.shape[1]):             # 迭代seq_len次

    pred, hidden_prev = model(input, hidden_prev)
    input = pred                        # 预测出的(下一个点的)序列pred当成输入(或者直接写成input, hidden_prev = model(input, hidden_prev))
    predictions.append(pred.detach().numpy().ravel()[0])


x = x.data.numpy()
y = y.data.numpy()
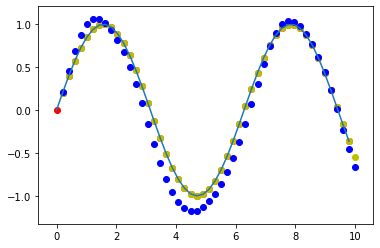
plt.plot(time_steps[:-1], x.ravel())

plt.scatter(time_steps[:-1], x.ravel(), c='r')     # x值
plt.scatter(time_steps[1:], y.ravel(), c='y')      # y值
plt.scatter(time_steps[1:], predictions, c='b')    # y的预测值
plt.show()

Iteration: 0 loss 0.47239747643470764
Iteration: 1000 loss 0.0028104630764573812
Iteration: 2000 loss 0.00022502802312374115
Iteration: 3000 loss 0.00013326731277629733
Iteration: 4000 loss 0.00011971688218181953
Iteration: 5000 loss 0.00046832612133584917

3. 梯度裁剪

如果发生梯度爆炸，在上面代码loss.backward() 与 optimizer.step() 之间要进行梯度裁剪：

    model.zero_grad()
    loss.backward()
    # 梯度裁剪
    for p in model.parameters():
        # print(p.grad.norm())                 # 查看参数p的梯度
        torch.nn.utils.clip_grad_norm_(p, 10)  # 将梯度裁剪到小于10
    optimizer.step()