Transformer
最近看了Attention Is All You Need这篇经典论文。论文里有很多地方描述都很模糊,后来是看了参考文献里其他人的源码分析文章才算是打通整个流程。记录一下。
Transformer整体结构
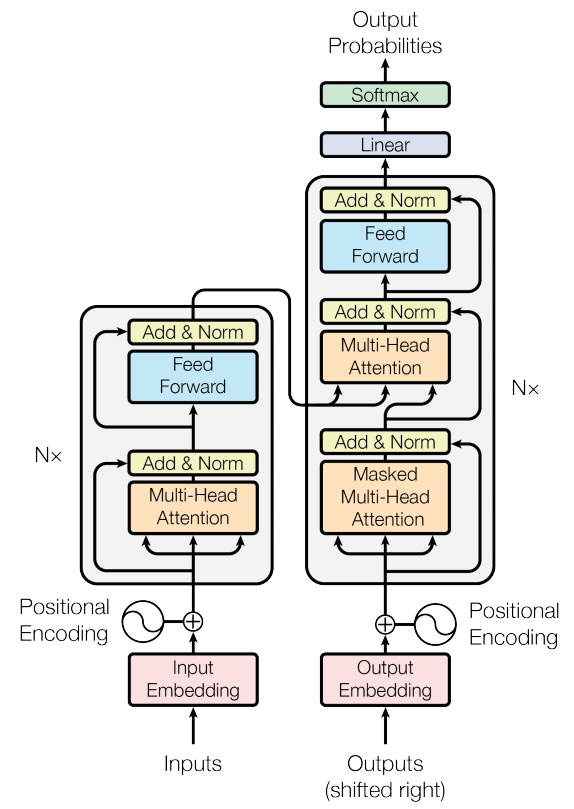
数据流梳理
符号含义速查
N: batch size
T: 一个句子的长度
E: embedding size
C: attention_size(num_units)
h: 多头header的数量
1. 训练
1.1 输入数据预处理
翻译前文本,翻译后文本,做长度截断或填充处理,使得所有语句长度都固定为T。
获取翻译前后语言的词库,对少出现词做剔除处理,词库添加< PAD >, < UNK >, < Start >, < End >四个特殊字符。
翻译前后文本根据词库,将文本转为id。
设batch_size=N, 则转换后翻译前后数据的size为:X=(N, T), Y=(N, T)
1.2 Encoder
前面结构图中Encoder的输入Inputs就是1.1中转换好的X。
1.2.1 Input Embedding
设输入词库大小为vocab_in_size, embedding的维度为E,则先随机初始化一个(vocab_in_size, E)大小的矩阵,根据embedding矩阵将X转换为(N, T, E)大小的矩阵。
1.2.2 Positional encoding
Position embedding矩阵维度也是(N,T,E),不同batch上,在T维度上相同位置的值一样。论文里用了三角函数sin和cos。
将Position embedding直接叠加到1.2.1的X上就是送入multi-head attention的输入了。
1.2.3 Multi-Head Attention
线性变换
将输入X=(N,T,E)通过线性变换,将特征维度转换为C。经过转换维度为X=(N,T,C)。
转为多头
沿特征方向平分为h份,在batch维度上拼接,方便后面计算。转换后维度X=(h*N, T, C/h)
计算(QK^T)
这里query(Q)和key(K)都是前面的X,计算后维度out=(h*N,T,T)
Mask Key
将out矩阵中key方向上原始key信息为0的部分mask掉,另其为一个极大的负数。所谓信息为0是指文本中PAD的部分。最开始会将PAD的embedding设为全0矩阵。
Softmax
把上一步的输入做softmax操作,变为归一化权值。维度(h*N,T,T)
Mask Query
把query部分信息量为0对应的维度置0。即这一部分的权重为0。信息量为0同样指PAD。
乘以value
self attention的value也就是上面的X(h*N, T, C/h),相乘后维度=(h*N, T, C/h)
reshape
将多头的部分恢复原来的维度,处理后维度out=(N, T, C)
1.2.4 Add & Norm
残差操作,out = out+X 维度(N, T, C)
layer norm归一化,维度(N, T, C)
多个block
上面1.2.3和1.2.4操作重复多次,最后一层的输出就是Encoder的最终输出。记为Enc。
1.3 Decoder
这里大部分跟前面Encoder是一样的。前面结构图中Decoder的输入Outputs就是1.1中转换好的Y。
1.3.1 output Embedding
设输入词库大小为vocab_out_size, embedding的维度为E,则先随机初始化一个(vocab_out_size, E)大小的矩阵,根据embedding矩阵将Y转换为(N, T, E)大小的矩阵。
1.3.2 Positional encoding
见1.2.2
1.3.3 Masked Multi-Head Attention
跟1.2.3基本相同,只是多了一个Mask步骤
线性变换
将输入Y=(N,T,E)通过线性变换,将特征维度转换为C。经过转换维度为Y=(N,T,C)。
转为多头
沿特征方向平分为h份,在batch维度上拼接,方便后面计算。转换后维度Y=(h*N, T, C/h)
计算(QK^T)
这里query(Q)和key(K)都是前面的Y,计算后维度out=(h*N,T,T)
Mask Key
将out矩阵中key方向上原始key信息为0的部分mask掉,另其为一个极大的负数。所谓信息为0是指文本中PAD的部分。最开始会将PAD的embedding设为全0矩阵。
Mask当前词之后的词
做这一步的原因是在解码位置i的词时,我们只知道位置0到i-1的信息,并不知道后面的信息。处理方式是将T_k>T_q部分置为一个极大的负数。T_k表示key方向维度,T_q表示query方向维度。
Softmax
把上一步的输入做softmax操作,变为归一化权值。维度(h*N,T,T)
Mask Query
把query部分信息量为0对应的维度置0。即这一部分的权重为0。信息量为0同样指PAD。
乘以value
self attention的value也就是上面的X(h*N, T, C/h),相乘后维度=(h*N, T, C/h)
reshape
将多头的部分恢复原来的维度,处理后维度out=(N, T, C)
1.3.4 Add & Norm
残差操作,out = out+X 维度(N, T, C)
layer norm归一化,维度(N, T, C)
1.3.5 Multi-Head Attention
跟之前的区别在于,以前是self attention,这里query是上面decode的输出dec, key是encoder的输出enc
转为多头
将dec沿特征方向平分为h份,在batch维度上拼接,方便后面计算。转换后维度dec=(h*N, T, C/h)
计算(QK^T)
这里query(Q)=dec和key(K)=enc,计算后维度out=(h*N,T_q,T_k)
Mask Key
将out矩阵中key方向上原始key信息为0的部分mask掉,另其为一个极大的负数。所谓信息为0是指文本中PAD的部分。最开始会将PAD的embedding设为全0矩阵。
Softmax
把上一步的输入做softmax操作,变为归一化权值。维度(h*N,T_q,T_k)
Mask Query
把query部分信息量为0对应的维度置0。即这一部分的权重为0。信息量为0同样指PAD。
乘以value
self attention的value也就是上面的enc(h*N, T, C/h),相乘后维度=(h*N, T_q, C/h)
reshape
将多头的部分恢复原来的维度,处理后维度out=(N, T_q, C)
1.3.6 Add & Norm
残差操作,out = out+dec 维度(N, T_q, C)
layer norm归一化,维度(N, T_q, C)
多个block
上面1.3.3-1.3.6重复多次
全连接变换
将上面输出结果(N, T_q, C)转换为(N, T_q, vocab_out_size)维,softmax获取每个位置输出各个词的概率。通过优化算法迭代更新参数。
2. 测试
测试时的Encoder部分比较好理解,跟训练时处理一样。只不过参数都是训练好的,比如embedding矩阵直接使用前面训练好的矩阵。
主要问题是在decoder的输入上。
对于一个语句,decoder一开始输入全0序列。表示什么信息也不知道(或者一个Start标签,表示开始)。经过一次decoder后输出一个长度为T的预测序列out1
第二次,输入out1预测的第一个字符,后面是全0,表示知道一个词了。经过decoder处理后,获得长度为T的输出预测序列out2
第三次,输入out2预测的前两个字符,后面是全0,表示知道2个词了。
依次类推。
注意,训练时decode结果是一次性获取的。但是测试的时候一次只获取一个词。需要类似RNN一样循环多次。
对于Position Embedding的理解
有些词颠倒一下顺序,含义是会变化的。
比如:奶牛 -> dairy cattle
如果没有添加位置信息,颠倒后会翻译成 牛奶 -> cattle dairy。
但这显然是不对的,在颠倒顺序后词的含义改变了, 应该翻译为 milk。
为了处理这种问题,所以需要加入位置信息。
参考文献
- https://blog.csdn.net/mijiaoxiaosan/article/details/74909076
- https://github.com/Kyubyong/transformer
- 《Attention Is All You Need》