重新写了之前的I,这是中期答辩我写的桥段,没用上就放到博客里来了。有意向了解的朋友们可以去看看另外几篇详述的。密码是123456
一个简易的室内路径规划基础模型
作者:dragonbean
1.1 选择编程工具
编程语言选择Python,语法简单易上手。选择Python的turtle库来实现绘制地图以及展示机器人“动态规划路径”的过程。
1.2 构建地图信息并绘制地图
采用矩形来描述室内障碍物,在室内平面图添加平面坐标系,用点的方式来定位障碍物和机器人。
下面是自己添加的一些障碍物的点坐标
'''author:https://www.cnblogs.com/dragonbean/
'''
class_allpoints = [[(80, 380), (80, 270), (0, 270), (0, 380)],
[(270, 200), (270, -70), (180, -70), (180, 200)],
[(-100, -100), (-100, -350), (-350, -350), (-350, -100)],
[(-20,50),(100,50),(100,-200),(-20,-200)],
[(-150,300),(-10,300),(-10,150),(-150,150)],
[(140,-90),(200,-90),(200,-160),(140,-160)],
[(-200,0),(-90,0),(-90,60),(-200,60)]
]
下面是用turtle库对上述障碍物点进行绘制的Python代码,都进行了一般化处理,后期修改或是使用都会很方便。
'''author:https://www.cnblogs.com/dragonbean/
'''
import turtle
__turtle = turtle.Turtle()
__turtle.hideturtle()
__turtle.speed(0)
#pointsList: [[point,point,point,...],[point,point,..],...]
def drawPolygons(pointsList,color='black',width=2):
if isinstance(pointsList,list) and isinstance(pointsList[0],list):
__turtle.width(width)
__turtle.color(color)
for each in pointsList:
__draw(each,style="polygon")
else:
print("date error!")
#pointsList: [point,point,point,...]
def drawRoad(pointsList,color="blue",width=1,speed=1):
__turtle.width(width)
__turtle.color(color)
__turtle.speed(speed)
__draw(pointsList,style=None)
#pointsList: [point,point,point,...]
def __draw(pointsList,style):
__turtle.penup()
__turtle.goto(pointsList[-1] if style=="polygon" else pointsList[0])
__turtle.pendown()
for point in pointsList:
__turtle.goto(point)
__turtle.penup()
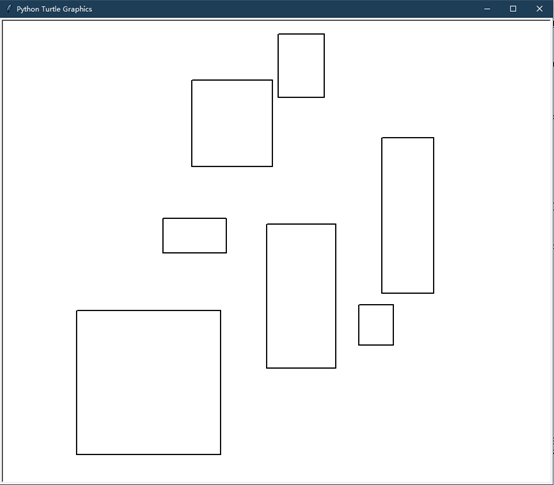
运行结果【室内障碍物】
1.3 设计算法
1.3.1递归
1.3.1.1 原型
以一种现有的通过深层迭代求解最短路径的路径搜索算法为原型进行改进:
'''author:https://www.cnblogs.com/dragonbean/
'''
def searchPath(graph, start, end):
results = []
__generatePath(graph, [start], end, results)
results.sort(key=lambda x:len(x))
return results
def __generatePath(graph, path, end, results):
current = path[-1]
if current == end:
results.append(path)
else:
for n in graph[current]:
if n not in path:
__generatePath(graph, path+[n], end, results)
def showPath(results):
print('The path from ', results[0][0], 'to' , results[0][-1], 'is :')
for path in results:
print(path)
if __name__=='__main__':
graph = {'a':['b','c','d'],
'b':['e'],
'c':['d','f'],
'd':['b','e','g'],
'e':['d'],
'f':['d','g'],
'g':['e']}
r1 = searchPath(graph, 'a', 'g')
showPath(r1)
1.3.1.2 改进
这个算法的思想有点像狄克斯特拉算法。将各节点间的权重进行相加,以最小成本路径作为最优规划路径的。但它的执行对象是节点,对于室内场景而言,障碍物是有大小和形状的,不能被看作是一个节点,因此我们重新定义节点:各个障碍物(矩形)的四个顶点作为节点,路径只能存在于各个障碍物的顶点之间。
现在就可以将上面这个算法进行以下改进:
1) 各个节点都是一个障碍物顶点对象,以坐标表示。
2) 节点间的成本就是节点间的距离,用两点间距离公式进行计算。
于是得到了下面的算法:
'''author:https://www.cnblogs.com/dragonbean/
'''
import math
def __searchPath(graph, start, end):
results = []
__generatePath(graph, [start,0], end, results)
results.sort(key=lambda x:x[-1])
return results
def __generatePath(graph, path, end, results):
current = path[-2]
if current == end:
results.append(path)
else:
for n in graph[current]:
if n not in path:
distance = path[-1] + math.sqrt((n[0]-path[-2][0])**2 + (n[1]-path[-2][1])**2) #增量计算不同路径的距离
__generatePath(graph, path[:-1]+[n,distance], end, results)
def showPath(results):
print('The path from ', results[0][0], 'to' , results[0][-1], 'is :')
for path in results:
print(path)
graph = {(-360,-360):((-350,-100),(-350,-350),(-100,-350)),
(-350,-100):((-350,-350),(-100,-100),(0,380),(0,270),(80,270),(180,200),(180,-70),(270,-70)),
(-350,-350):((-350,-100),(-100,-350)),
(-100,-350):((-350,-350),(-100,-100),(0,380),(0,270),(80,270),(180,200),(180,-70),(270,-70)),
(-100,-100):((-350,-100),(-100,-350),(0,380),(0,270),(80,270),(180,200),(180,-70),(270,-70)),
(0,380):((0,270),(80,380)),
……,
(0,270):((80,270),(180,200),(180,-70),(270,200)),
(80,270):((180,200),(180,-70),(270,200)),
(80,380):((180,200),(180,-70),(270,200)),
(180,200):((180,-70),(270,200)),
(180,-70):((180,200),(270,-70)),
(270,-70):((180,-70),(270,200),(300,150)),
(270,200):((180,-70),(270,-70),(300,150))
}
1.3.1.3 不足
这个算法在性能上和复用上都存在着极大的问题,可以说很差劲。
首先在性能上,为了简化编程复杂度,算法采用了递归的形式,当递归深度达到一定值后,运算速度会大幅下降运算时间呈指数增长。经过测试,发现当障碍物只有3个时运算速度为1-2秒,而再多添加一个障碍物运算时间就已经大于10分钟了。
其次是这个显眼的graph字典,它是这个算法的动力来源,规定了哪些节点可以到哪些节点,不能到哪些节点,而这些数据都需要人为创造、人工输入。这种数据类型也是造成上述性能差的最主要原因。
1.3.1.4 改进
对于性能方面,我们提出的改进方案是进行浅层递归,也就是降低递归深度。具体的做法有两种思路:
1) 选择起始位置到目标位置之间距离的1.5倍-3倍不等的值作为继续递归的真条件,一旦递归过程中已走过的距离大于这个值就本条递归执行下一条递归。
2) 针对1)的不完美,可以先进行一次无约束的寻路,先找到一条可行的路径(不一定是最优的),将这条路径的距离作为继续递归的真条件。
并且基于此我们还给出了另一种(两个)动态的寻找局部最优路径的算法(第二个是对第一个的改进):
'''author:https://www.cnblogs.com/dragonbean/
'''
def solution_two(start, end, graph):
print(graph)
#还阔以再优化,再计算多一个点,就更趋于最优了
def __findNext(start,end,graph, path):
minDistance = [None,None]
for each in graph[start]:
if each == end:
path.append(end)
return
else:
distance = math.sqrt((each[0]-start[0])**2+(each[1]-start[1])**2)+math.sqrt((end[0]-each[0])**2+(end[1]-each[1])**2)
if minDistance[1]==None or minDistance[1]>distance:
minDistance = [each,distance]
print(minDistance[0])
path.append(minDistance[0])
__findNext(minDistance[0],end, graph, path)
path = [start]
__findNext(start, end, graph, path)
print(path)
return path
def solution_three(start, end, graph):
def __findNext(start,end,graph, path):
minDistance = [None,None]
for each in graph[start]:
if each in path:
continue
elif each == end:
path.append(end)
return
next_min_distance = None
tmp_list = graph[each][:]
try:
tmp_list.remove(start)
print(start)
print(tmp_list)
except:
pass
for i in tmp_list:
if i == end:
path.extend([each,i])
return
next_distance = math.sqrt((end[0]-i[0])**2+(end[1]-i[1])**2) + math.sqrt((i[0]-each[0])**2+(i[1]-each[1])**2)
if next_min_distance==None or next_min_distance>next_distance:
next_min_distance = next_distance
distance = next_min_distance + math.sqrt((each[0]-start[0])**2+(each[1]-start[1])**2)
if minDistance[1]==None or minDistance[1]>distance:
minDistance = [each,distance]
path.append(minDistance[0])
__findNext(minDistance[0],end, graph, path)
path = [start]
__findNext(start, end, graph, path)
print(path)
return path
不论是限制递归层数的方法还是动态选择局部最优的方法,都可以极大的保持算法的高性能,但是仍不能解决人为创造、人工输入的麻烦,因此我们开始了漫漫长征路。
1.3.2可视化
1.3.2.1 前世今生
可视化这个词是在查找路径规划算法的时候邂逅的,很形象。为了解决人为创造、人工输入的麻烦,我们借用可视化来给已有的算法提供它所需要的graph字典。
1.3.2.2 理解可视化
首先我们来理解一下可视化,我们之所以能看到一个东西,是因为我们的眼睛和被看物体之间没有任何障碍物。也就是说,对于一个观察点而言,它和某个被观察点之间没有东西挡着,那么这个被观察点对于观察点而言就是可视的,反之则是不可视的。
在我们所处的这种场景中,可视和不可视的情况大致可分为三种:

在地图上任选一个观测点,最多只能看到障碍物的三个顶点,又由于障碍物和障碍物之间存在遮挡关系(如图中的半遮挡),因此这部分处理还需精心设计。
1.3.2.3 算法实现
为了让程序可以“理解”可视与不可视的概念,我们采用角度区间和距离远近这两个量度来做对比进行判断,来判断某个被观察点对于一个观察点来说可视与否。可以通过下面这张图来理解:
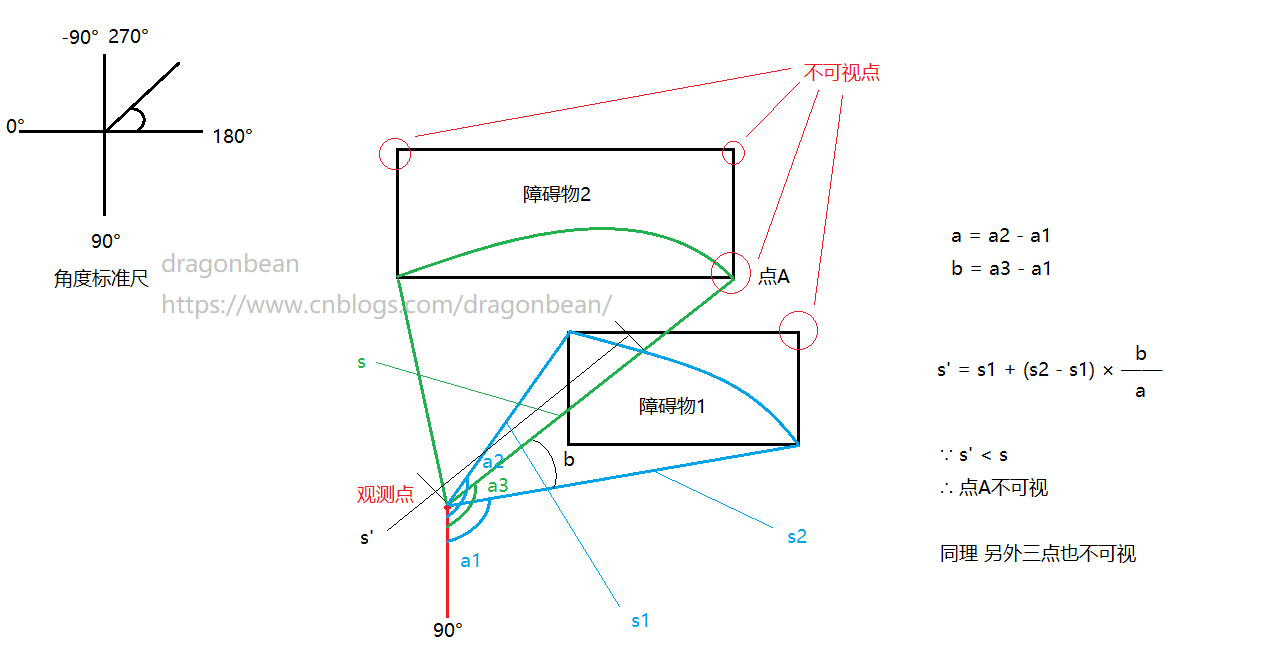
这个设计的巧妙之处在于,抽象了一个障碍物角度区间,角度区间内的每一个角度都对应一个距离长度,对于任何一个被观测点在已知障碍物角度区间上,该点和观测点的连线构成一个角度,只要该角度所对应的距离长度大于该点与观测点的距离,那么被观测点点就是可视的,反之是不可视的,即便在有很多障碍物的情况下,我们只要得到了障碍物角度区间,就可以对每一个被观测点(障碍物顶点)进行判断,判断其是否可视,将可视的点保存下来,不可视的点丢弃,这样就能生成一个graph字典。
但在获取所有障碍物角度区间和判断障碍物顶点是否可视的过程中,我们应当考虑把障碍物当成一个整体(类似于面向对象中类一样的东西),并且在判断的过程中优先和距离较近的障碍物角度区间进行比较,否则(如果和最远的障碍物角度区间进行比较)那么除了该障碍物上的不可视点以外,所有的其他障碍物上的所有被观测点都可视,因为所有点距离观测点的距离都小于角度区间下指定角度所对应的距离。
'''author:https://www.cnblogs.com/dragonbean/
'''
import math
import copy
def main(start, end, class_allpoints):
#对于所有的点的该点,判断是否在class_allpoints嵌套列表中,并深度复制成一个用于生成相对于该点的所有障碍物区间的点列表
#要生成障碍物区间的所有 该点 集
allpoints = [i for each in class_allpoints for i in each]
graph = dict()
if start not in allpoints:
allpoints.append(start)
if end not in allpoints:
allpoints.append(end)
for this_point in allpoints:
pop_allpoints = None
#深度拷贝一个用以产生障碍物区间的列表点集,该列表点集规避了一些漏洞(不会对 该点 进行拷贝)
for each in class_allpoints:
for i in each:
if i == this_point:
pop_allpoints = copy.deepcopy(class_allpoints)
pop_allpoints[class_allpoints.index(each)].remove(i)
break
if pop_allpoints:
break
pop_allpoints = pop_allpoints if pop_allpoints else copy.deepcopy(class_allpoints)
data = generateInterval(this_point, pop_allpoints)
graph[this_point] = judgeVisualPoints(this_point, pop_allpoints, data[0], end)
return graph
def generateInterval(this_point, pop_allpoints):
angleANDdistance = list()
angleANDpoint = list()
for each in pop_allpoints:
min_y = None #用于记录特殊情况下最底边到 该点 的距离
maxTmp = [None,None,None]
minTmp = [None,None,None]
for point in each:
tmp = (math.degrees(math.atan((point[1]-this_point[1])/(point[0]-this_point[0]))) if (point[0]-this_point[0]!=0) else -90 if (point[1]-this_point[1]>0) else 90)
tmp = tmp + 180 if point[0]-this_point[0]>0 else tmp #认为定义了角度的范围从-90~270,从正北方向逆时针转
#在遍历的基础上进行变量比较得到 最大和最小
maxTmp = [point,tmp,math.sqrt((point[1]-this_point[1])**2+(point[0]-this_point[0])**2)] if (maxTmp[1]==None or tmp > maxTmp[1]) else maxTmp
minTmp = [point,tmp,math.sqrt((point[1]-this_point[1])**2+(point[0]-this_point[0])**2)] if (minTmp[1]==None or tmp < minTmp[1]) else minTmp
#真是个头大的东西,这是一个特殊情况的粗暴处理(还是有很多问题,需要对跨270度的区间进行分开处理。!!!!!!!!!!!
# 问题解决了吧应该 我记得是解决了,,,我丢///)
if maxTmp[1]-minTmp[1] > 180 and (maxTmp[1]!=270 and minTmp!=0 or minTmp!=-90 and maxTmp!=180): #存在一种特例,当障碍物在起始点的正上方左右时,max_angle-min_angle不能表示障碍物区间
#对这种情况进行单独处理,一旦有点触发了这种情况(这里的特殊情况排除了特殊点为正上方障碍物的下面两个端点),就执行特殊代码,执行完后直接跳出该层循环,对下一个障碍物进行处理
#直接得到最大点和最小点(相对于角度而言)
maxPoint = (min(point[0] for point in each),min(point[1] for point in each))
minPoint = (max(point[0] for point in each),min(point[1] for point in each))
#为了和上面的一般情况统一,这里也用maxTmp和minTmp
maxTmp = [maxPoint,
(math.degrees(math.atan((maxPoint[1]-this_point[1])/(maxPoint[0]-this_point[0]))) if (maxPoint[0]-this_point[0]!=0) else -90),
math.sqrt((maxPoint[1]-this_point[1])**2+(maxPoint[0]-this_point[0])**2)]
minTmp = [minPoint,
(math.degrees(math.atan((minPoint[1]-this_point[1])/(minPoint[0]-this_point[0])))+180 if (minPoint[0]-this_point[0]!=0) else 270),
math.sqrt((minPoint[1]-this_point[1])**2+(minPoint[0]-this_point[0])**2)]
min_y = min(point[1] for point in each) #特殊情况下障碍物最底边距 该点 的距离
break
#对一般和特殊情况的最后一次分离处理,生成我们需要的区间
if min_y:
#将特殊情况下障碍物的区间 分开,因为其包含无穷大,所以也是从无穷大分开的
angleANDdistance.append([minTmp[1:],[270,min_y-this_point[1]]])
angleANDdistance.append([[-90,min_y-this_point[1]],maxTmp[1:]])
else:
#待删减(整个函数乃至整个代码)
angleANDdistance.append([minTmp[1:],maxTmp[1:]])
#记录角与点,用于后面的绘制可视区间
angleANDpoint.append([minTmp[:-1],maxTmp[:-1]])
return [angleANDdistance,angleANDpoint]
def judgeVisualPoints(this_point, pop_allpoints, angleANDdistance, end):
visualPoints = list()
sequentialPoints = sorted([i for each in pop_allpoints for i in each]+[end], key=lambda x:(x[0]-this_point[0])**2+(x[1]-this_point[1])**2)
for point in sequentialPoints:
#对新计算的角进行数据处理
angle = (math.degrees(math.atan((point[1]-this_point[1])/(point[0]-this_point[0]))) if (point[0]-this_point[0]!=0) else -90 if (point[1]-this_point[1]>0) else 90)
angle = angle + 180 if point[0]-this_point[0]>0 else angle
#用与判断点是否在区间,不再就返回false,在就返回所在区间对应的原始数据
tmp = __IsInIntervals(angle, angleANDdistance)
if tmp:
distance = (angle-tmp[0][0])/(tmp[1][0]-tmp[0][0])*(tmp[1][1]-tmp[0][1])+tmp[0][1]
if point == end and this_point == (270,-70):
print(point,angle,tmp,distance,math.sqrt((point[1]-this_point[1])**2+(point[0]-this_point[0])**2),sep="
")
if math.sqrt((point[1]-this_point[1])**2+(point[0]-this_point[0])**2) < distance:
visualPoints.append(point)
else:
visualPoints.append(point)
return visualPoints
def __IsInIntervals(angle,Raw_intervalsList):
#一个排序,把Raw_intervalsList按照最近距离进行排序(最远距离不行!!【如果最近距离也有问题的话,可以选择对全部区间遍历一遍,时间基本差不多吧、】),以保证算法依据人的想法正确运行,避免出现不可视点被加入可视点集
#因为总是前面的障碍物挡住后面的障碍物,这才导致某些点不可视
Raw_intervalsList.sort(key=lambda x: x[0][1] if x[0][1]<x[1][1] else x[1][1])
for each in Raw_intervalsList:
intervalsList = (each[0][0],each[1][0])
if angle>intervalsList[0] and angle<intervalsList[1]:
return each
else:
continue
return False
1.3.2.4 问题及改进
经过各种测试,发现这个可视化的算法仍存在问题:s’的计算方法有问题,图中的方法没有经过数学验证,实际得到的s’所组成的面积并不是图中所画的扇形,如:
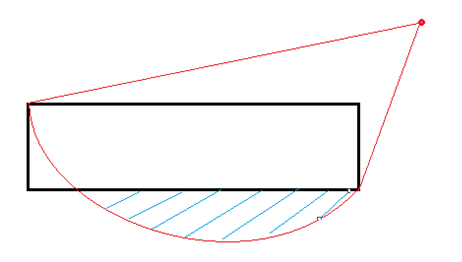
图中如果被观测点(非该障碍物上的其他障碍物顶点)落入蓝色阴影部分,那么就会将其纳入可视点的范围内去,有悖于实际情况。
因此我们需要通过严格的数学来找到真正能表达原图中曲线的方法。
转载请注明出:https://www.cnblogs.com/dragonbean