钢条切割

今天起床，清风徐来，迎接此题！

问题描述：切割一根钢条，不同的长度对应不同的售价，如何切割使得获得最大的利益。

Another decipition:

某公司购买钢条将其切割成锻钢条出售，切割过程本身没有支出，而钢条切割的长度不同价格不同，比如：
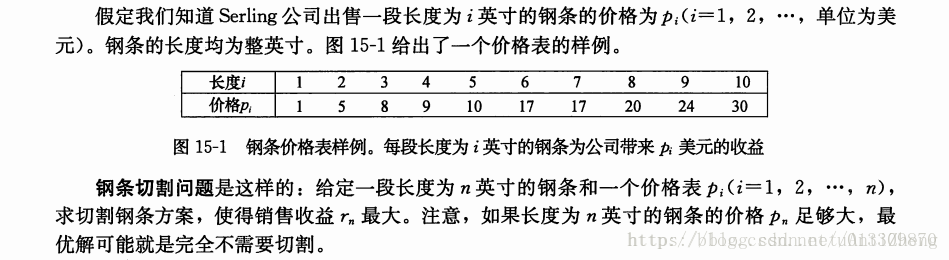
长度i 1 2 3 4 5 6 7 8 9 10
价格pi 1 5 8 9 10 17 17 20 24 30
给定一段长度为n的钢条和价格表，求使收益最大的钢条切割方案

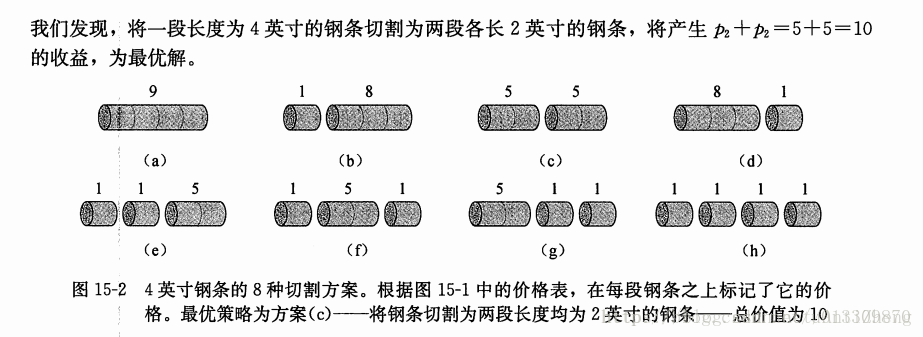
分析: 这是一个最优化问题，对于一般的n 用rn表示最大收益， rn = max{pn, r1+rn-1,r2+rn-2,…..rn-1+r1}; pn表示不切割的时候，其他表示切成两段，分别长i 和n-i，接着求解这两段的最优切割收益 这里为了求得原问题，先求形式完全一样但规模更小的子问题，即完成首次切割后，将切割出的两部分当做两个独立的实例，在组合子问题的最优解，在所有可能的两段切割方案中选取组合收益最大的，构成原问题的最优解。 所以钢条切割问题有最优子结构性质:问题的最优解由相关子问题的最优解组合而成，而这些子问题可以独立求解.

钢条切割问题还存在一种思路上更为简单的递归方式： 
将钢条从左边切割下长度为i 的一段，只对右边的n-i长度的进行递归切割，所以rn = max(pi + rn-i); (左边一段的加上右边的最大收益)这样最优解只包含一个子问题 

Reference 1:  https://blog.csdn.net/liu798675179/article/details/52997987

Reference 2:https://blog.csdn.net/jianfpeng241241/article/details/51855214

Relationships:https://download.csdn.net/download/qq_42324327/11156405

Resauces Taken:

我们可以用拉格朗日乘数法，求解给定条件下的方程最优解，同样，动态规划算法也是用于在一定条件下的求解最优解的方法

 

 

 一些参考：

# 自下而上的动态规划
def cutMemo(p, n):
    r = [0] * (n+1)
    for i in range(1, n+1):
        if n == 0:
            return 0
        q = 0
        for j in range(1, i+1):
            q = max(q, p[j-1]+r[i-j])
            r[i] = q
    return r