民生问题C++

目录

• 题目
  • 题目描述：
  • 输入输出样例:
  • 数据范围：
  • 附上民生问题原题
  • 附上测评系统
• 思路
  • 思路
  • 测评结果
• 代码

题目

项目问题 (就是民生问题,一模一样)
注:题目来自东莞2019年特长生测试第2题

题目描述：

张三是某项目工程总经理，在工程开发时遇到了 n 个问题，张三的团队中共
有 w 人，每一个人都有自己的特长，由于还有其他工作要做,希望解决这 n 个问
题最尽安排最少的人员，现在张三想知道至少安排多少个人,才能把所有的问题 都解决?
数据输入：
从文件 question.in 中读入数据，第一行两个整数 n、w 表示有 n 要解决的
问题和张三的员工有 w 人，要解决的问题以 1..n 编号。接下来 w 行，第 i+1 行
第一个数 li 表示第 i 个人能解决问题的数量，接下来 li 个数表示第 i 个人能解
决的问题的编号。
数据输出：
将结果输出到文件 question.out 中，只有一个数，表示至少要安排的人数。
3

输入输出样例:

question.in
4 4
2 1 2
1 4
3 2 3 4
2 1 3
question.out
2

数据范围：

对于 40%的数据,3<=n,w<=10
对于 100%的数据,3<=n,w<=60,1<=li<=6

附上民生问题原题

(题目来源:https://oj.dgzx.net/front/problem/ToProblemDetailBlank/3637)

【问题描述】
某市政府非常关注民生，最近对民生问题作了调研，提出了最近要解决的n个民生问题，政府的专家顾问组有w人，每一个专家都有自己的特长，政府知道每专家能解决哪些问题,现在政府想知道至少请多少位专家,才能把所有的问题都解决?
输入输出格式
输入格式：
从文件question.in中读入数据，第一行两个整数n、w表示有n要解决的问题和w位专家，要解决的问题以1..n编号。接下来w行，第i+1行第一个数li表示第i位专家能解决问题的数量，接下来li个数表示第i位专家能解决的问题的编号。
输出格式：
将结果输出到文件question.out中，只有一个数，表示至少要请多少位专家。
样例输入输出同上

附上测评系统

https://www.luogu.com.cn/problem/U127339

思路

思路

第一眼看到这题,搜啊!!!
看到数据范围,沉默......(貌似 不能过)
但是,正解就是搜索加了一堆剪枝

先说说搜索的剪枝,分为可行性剪枝和最优性剪枝.
显然,可以用到常规的最优性剪枝(并不难想到):如果当前选择的专家数 > 当前最优值,直接return.
其次,就是不常规的剪枝:

1. 如果专家a能解决的问题,专家b都能解决,那么专家a可以不纳入搜索范围
2. 如果一个问题,只有专家a可以解决,那么专家a必选,同时不纳入搜索范围

说完剪枝,就是怎么搜的问题:

1. 枚举每一个(这里指搜索范围以内的专家)专家选还是不选,直到所有问题被解决或已经遍历完所有专家(我一开始就是这样的)
2. 枚举每一个未解决的问题选择哪一个专家,顺便标记该专家能解决的其它问题(有点拗).从第一个问题枚举到最后一个问题,同时跳过已解决的问题

显然,第二种效率更高
别问我这些都是怎么想到的(老师讲的~ )
另外,这题确实比较麻烦,要一步步来,不要急

测评结果

完整版测评结果:

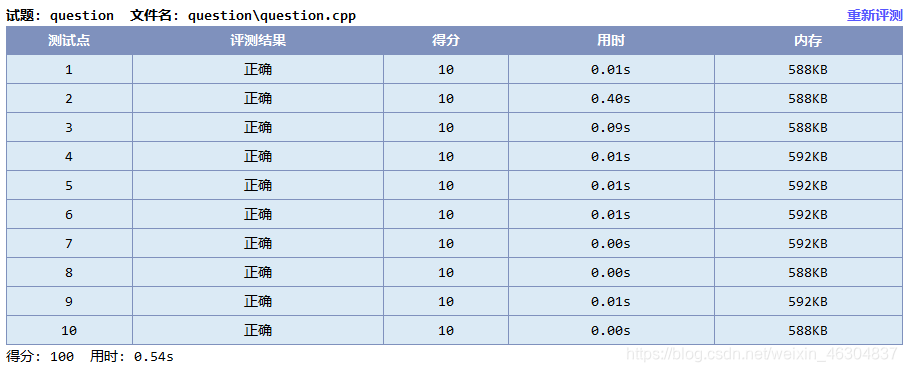
去掉最优性剪枝测评结果:

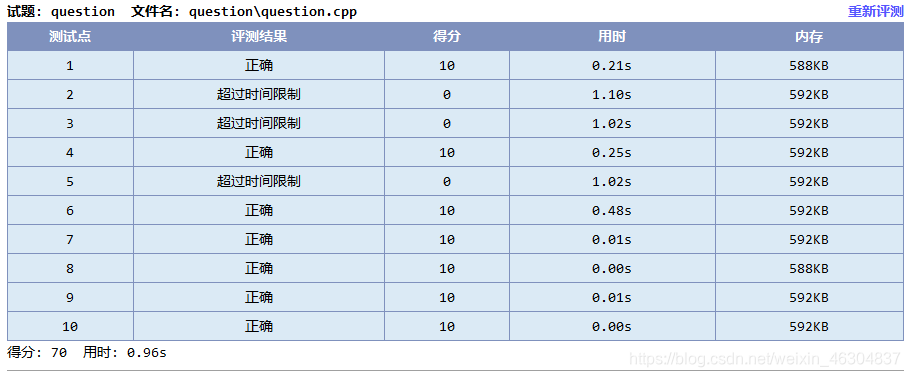
去掉剪枝1(专家之间的包含关系)测评结果:

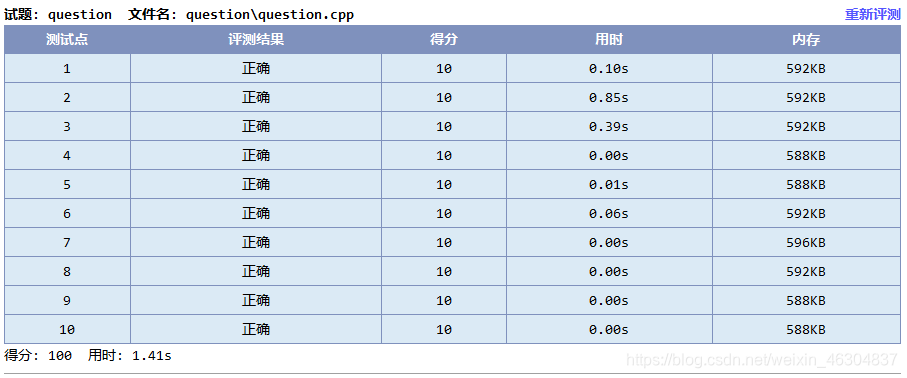
去掉剪枝2(能解决问题的唯一专家)测评结果:

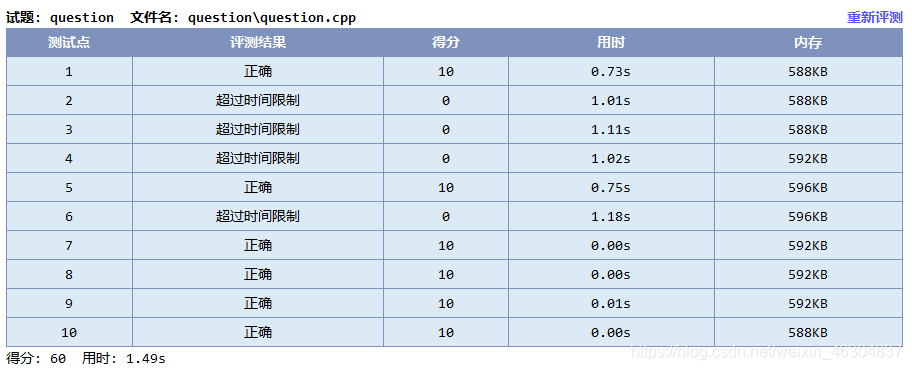
代码

#include <iostream>
#include <cstdio>
using namespace std;
int n , m , sum , ans , sol[110];
//sol[i]:问题i是否被解决(注意int类型,往下看就知道了) 
bool map[110][110], out[110];
//map[i][j]:false:i专家不能解决j问题,true:能解决,out[i]:i专家是否在搜索范围以内(true表示已经被踢出(不在范围内))
int p[110][110] , pn[110];//p[i][j]:i问题能被j专家解决(链表) ,pn[i]为能解决i问题的专家数量 
int q[110][110] , qn[110];//q[i][j]:i专家能解决j问题(链表) 
void dfs(int x , int nowsum){
	if(x == m + 1){
		if(nowsum < ans)
			ans = nowsum;
		return;
	}
	if(nowsum >= ans)//最优性剪枝 
		return;
	
	for(int i = 1 ; i <= pn[x] ; i++){
		for(int j = 1 ; j <= qn[p[x][i]] ; j++)
			sol[q[p[x][i]][j]]++;
			//这里注意:sol[i]表示当前能解决i问题的专家数量,sol[i]==0则i问题未解决,仔细想想为什么这样 
		
		int nex = x + 1;//同样,避免多次递归,提高效率 
		while(sol[nex] != 0 && nex <= m)nex++;
		dfs(nex , nowsum + 1);
		
		for(int j = 1 ; j <= qn[p[x][i]] ; j++)//回溯 
			sol[q[p[x][i]][j]]--;
	}
}
int main(){
	freopen("question.in" ,"r" , stdin);
	freopen("question.out" ,"w" , stdout);
	//input
	cin >> m >> n;
	for(int i = 1 ; i <= n ; i++){
		cin >> qn[i];
		for(int j = 1 ; j <= qn[i] ; j++){
			cin >> q[i][j];
			map[i][q[i][j]] = true;
		}
			
	}
	//判断包含关系 
	for(int i = 1 ; i <= n ; i ++)
		if(!out[i])
			for(int j = 1 ; j <= n ; j++)//判断i专家能解决的问题是否包含j专家 
				if(i != j && !out[j]){
					bool b = false;
					
					for(int k = 1 ; k <= m ; k++)
						if(!map[i][k] && map[j][k]){
							b = true;
							break;
						}
					if(!b){
						out[j] = true;
					}
				}
	//判断问题的唯一解  
	for(int i = 1 ; i <= m ; i ++){
		if(sol[i] > 0)
			continue;
		int k = -1;
		bool b = false;
		
		for(int j = 1 ; j <= n ; j ++)
			if(map[j][i] && !out[j]){
				if(k != -1){
					b = true;
					break;
				}
				k = j;
			}
		if(b == false){
			out[k] = true;
			sum ++;
			for(int j = 1 ; j <= m ; j++)//标记该专家能解决的问题 
				if(map[k][j])
					sol[j] += 1;
		}
			
	}
	//未解决的问题和 搜索范围内的专家建立链表(效率更高) 
	for(int i = 1 ; i <= n ; i++)
		if(!out[i])
			for(int j = 1 ; j <= m ; j ++)
				if(map[i][j]){
					pn[j]++;
					p[j][pn[j]] = i;
				}
	
	int beg = 1;//找到第一个没解决的问题,避免多次递归 
	while(sol[beg] != 0 && beg <= m)beg++;
	ans = 10000;
	dfs(beg , sum);
	cout << ans;
	return 0;
}