「数据结构」第3章 RMQ问题课堂过关

目录

• A. 【例题1】数列区间
  • 题目
  • code
• B. 【例题2】静态区间
  • 题目
  • code
• C. 【例题3】与众不同
  • 题目
  • 思路
  • code
• D. 【例题4】矩阵最值
  • 题目
  • 思路
  • code

「数据结构」第3章 RMQ问题课堂过关

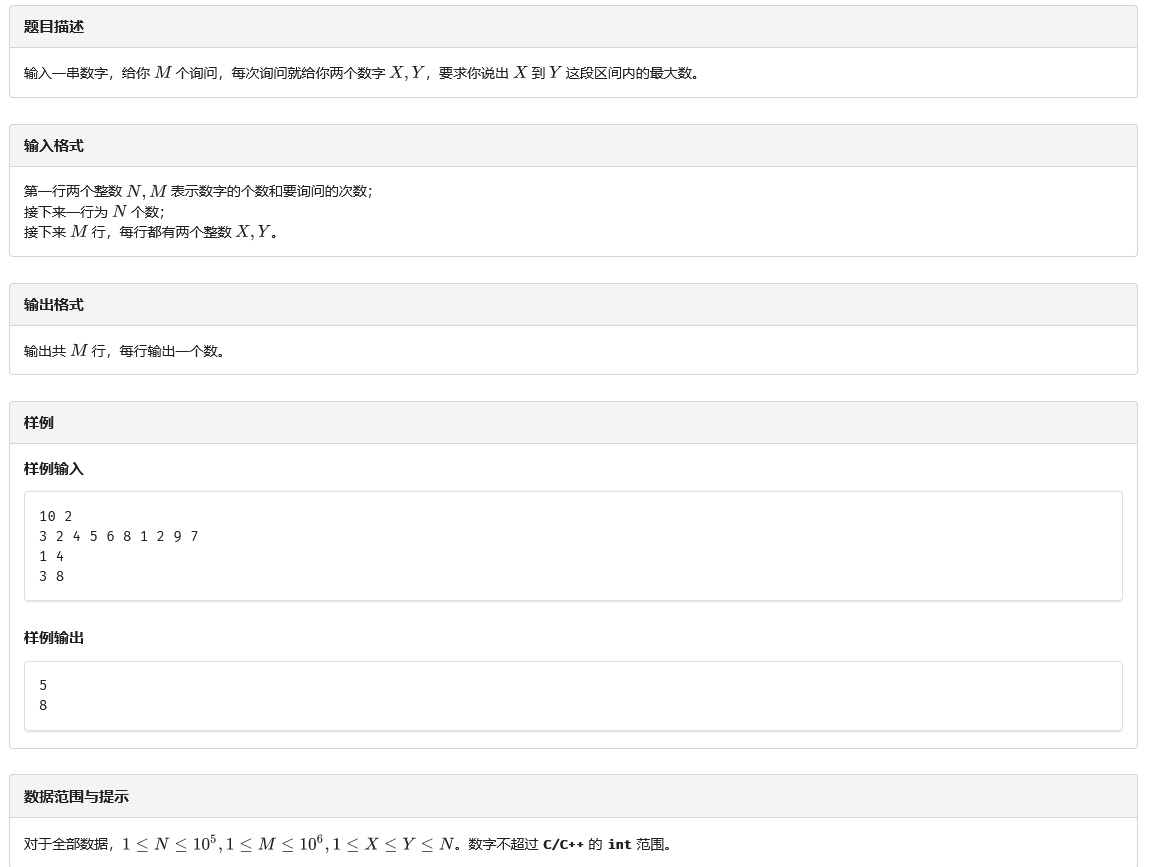
A. 【例题1】数列区间

题目

code

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>

#define nn 100010
using namespace std;
int read() {
	int re = 0;
	char c = getchar();
	while(c < '0' || c > '9')c = getchar();
	while(c >= '0' && c <= '9')
		re = (re << 1) + (re << 3) + c - '0',
		c = getchar();
	return re;
}

int n , m;
int st[nn * 2][25];
inline int max_(int a , int b) {return a > b ? a : b;}
int main() {
	memset(st , 0x81 , sizeof(st));
	
	n = read();	m = read();
	for(int i = 1 ; i <= n ; i++)
		st[i][0] = read();
	
	int k = log(n) / log(2) + 1;
	for(int j = 1 ; j <= k ; j++) {
		for(int i = 1 ; i <= n ; i++) {
			st[i][j] = max_(st[i][j - 1] , st[i + (1 << j - 1)][j - 1]);
		}
	}
	while(m--) {
		int l = read() , r = read();
		k = log(r - l + 1) / log(2);
		printf("%d
" , max_(st[l][k] , st[r - (1 << k) + 1][k]));
	}
	return 0;
}

---

B. 【例题2】静态区间

题目

code

#include <iostream>
#include <cstdio>
#include <cmath>
#define N 50010
using namespace std;
int read() {
	int re = 0;
	char c = getchar();
	bool sig = false;
	while(c < '0' || c > '9') {
		if(c == '-')	sig = true;
		c = getchar();
	}
	while(c >= '0' && c <= '9')
		re  = (re << 1) + (re << 3) + c - '0' , c = getchar();
	return sig ? -re : re;
}
int n , m;
int st[N * 2][25];
int gcd(int a , int b) {
	if(a == 0) return b;
	return b == 0 ? a : gcd(b , a % b);
}
int main() {
	n = read() , m = read();
	for(int i = 1 ; i <= n ; i++)
		st[i][0] = read();
	
	for(int j = 1 ; (1 << j) <= n ; j++)
		for(int i = 1 ; i <= n ; i++)
			st[i][j] = gcd(st[i][j - 1] , st[i + (1 << j - 1)][j - 1]);
			
	for(int i = 1 ; i <= m ; i++) {
		int l = read() , r = read();
		int k = log(r - l + 1) / log(2);
		printf("%d
" , gcd(st[l][k] , st[r - (1 << k) + 1][k]));
	}
	return 0;
}

---

C. 【例题3】与众不同

题目

思路

说明:这题我的方法是线段树而非RMQ

做法比较奇妙,结合代码讲下:

//读入
	n = read() , m = read();
	segt.root = segt.build(1 , n);
	for(int i = 1 ; i <= n ; i++)
		a[i] = read();//原数据存储的数组
	for(int i = 1 ; i <= m ; i++)//询问
		q[i].l = read() + 1 , q[i].r = read() + 1 , q[i].id = i;
	
	sort(q + 1 , q + m + 1 , cmp);//按照询问的右端点排序
	Discretize(a + 1 , a + n + 1);//离散化

不难想到,从(i)位置开始,最长的完美序列长度是可以(O(n))求出来的:

	for(int i = 1 , p = 0 ; i <= n ; i++) {
		while(p < n && vis[a[p + 1]] == false)
			vis[a[p + 1]] = true , ++p;
		r[i] = p;//[i,r[i]]这一段为完美序列,且r[i]最大
		vis[a[i]] = false;
	}

处理每一个询问并输出,先贴出代码(主程序就这么短啦):

	for(int i = 1 , p = 0 ; i <= m ; i++) {
		while(p <= n && r[p + 1] <= q[i].r)
			++p , segt.change2(segt.root , p , r[p] - p + 1);//对p单点修改(直接修改值而不是加上一个东西)
			
		segt.change(segt.root , p + 1 , n , q[i].r - q[i - 1].r);//对[p+1,n]区间修改(直接加上一个东西)
		ans[q[i].id] = segt.ask(segt.root , q[i].l , q[i].r);//最大值查询
	}
	
	for(int i = 1 ; i <= m ; i++)
		printf("%d
" , ans[i]);

下面做解释:

设(dat_i)表示当前从(i)开始的最长"完美序列"长度((dat_i+i-1)不得大于当前右边界)

我们在上面把询问按照右端点从小到大排序,思考,每一次右端点扩张会对(dat)造成什么影响?显然,有以下情况:(下面(i,j)的意义与代码中不同)

[dat_i=egin{cases} 0 &(i >q_j.r)\ q_j-i+1 &(q_{j-1}.r le i le q_j.r &andquad q_j.rge r_i)\ dat_i+q_j.r-q_{j-1}.r &(ile q_j.rle r_i &andquad ileq q_{j-1}.r )\ r_i-i+1 &(r_ile q_j.r)\ end{cases} ]

对于询问,直接输出区间内的最大值即可

不难看出,对于后面两种情况及查询操作,(dat)数组是可以用线段树维护的,为了方便第一,第二种情况,我们不妨赋初始值:(dat_i=1-i)(比较巧妙,自己体会一下)

把线段树,离散化,快读写上,就完成啦:

code

#include <iostream>
#include <cstdio>
#include <algorithm>
#define N 200010
#define M 200010
#define inf 0x3fffffff
using namespace std;
int read() {
	int re = 0;
	char c = getchar();
	bool sig = 0;
	while(c < '0' || c > '9') {
		if(c == '-')	sig = true;
		c = getchar();
	}
	while(c >= '0' && c <= '9')	re = (re << 1) + (re << 3) + c - '0' ,  c = getchar();
	return sig ? -re : re;
}
struct DiscretizeNode {//离散化begin
	int dat , id;
}tmp[N];
bool cmp_Dis(DiscretizeNode a , DiscretizeNode b) {
	return a.dat < b.dat;
}
void Discretize(int *a , int *ed) {
	int n = ed - a;
	for(int i = 0 ; i < n ; i++)
		tmp[i].dat = a[i] , tmp[i].id = i;
	sort(tmp , tmp + n , cmp_Dis);
	int cnt = 1;
	a[tmp[0].id] = 1;
	for(int i = 1 ; i < n ; i++)
		a[tmp[i].id] = (tmp[i].dat != tmp[i - 1].dat ? ++cnt : cnt);
}//离散化end
struct SegmentTree {//线段树begin
	struct basis {
		int l , r , ls , rs , max , tag;
	}tr[N * 4];
	#define l(_) tr[_].l
	#define r(_) tr[_].r
	#define ls(_) tr[_].ls
	#define rs(_) tr[_].rs
	#define tag(_) tr[_].tag
	inline int max_(int x , int y) {return x > y ? x : y;}
	int root;
	int build(int l , int r) {
		static int cnt = 0;
		int p = ++cnt;
		l(p) = l , r(p) = r;
		if(l == r) {
			tr[p].max = 1 - l;//这里的初始化
			return p;
		}
		int mid = (l + r) / 2;
		ls(p) = build(l , mid);
		rs(p) = build(mid + 1 , r);
		tr[p].max = max_(tr[ls(p)].max , tr[rs(p)].max);
		return p;
	}
	inline void spread(int p) {
		if(tag(p) == 0)	return;
		tr[ls(p)].max += tag(p);
		tr[rs(p)].max += tag(p);
		tag(ls(p)) += tag(p);
		tag(rs(p)) += tag(p);
		tag(p) = 0;
	}
	void change(int p , int l , int r , int dat) {//[l,r]值增加dat
		if(l > r(p) || r < l(p))	return;
		if(l <= l(p) && r >= r(p)) {
			tag(p) += dat;
			tr[p].max += dat;
			return;
		}
		spread(p);
		change(ls(p) , l , r , dat);
		change(rs(p) , l , r , dat);
		tr[p].max = max_(tr[ls(p)].max , tr[rs(p)].max);
	}
	void change2(int p , int id , int dat) {//将id位置改为dat
		if(l(p) == r(p)) {
			tr[p].max = dat;
			return;
		}
		spread(p);
		change2(l(rs(p)) <= id ? rs(p) : ls(p) , id , dat);
		tr[p].max = max_(tr[ls(p)].max , tr[rs(p)].max);
	}
	int ask(int p , int l , int r) {
		if(l > r(p) || r < l(p))	return -inf;
		if(l <= l(p) && r >= r(p))
			return tr[p].max;
		spread(p);
		return  max_(ask(ls(p) , l , r) ,  ask(rs(p) , l , r));
	}
}segt;//线段树end

struct query {
	int l , r , id;
}q[N];
bool cmp(query a , query b) {return a.r < b.r;}

int n , m ;
int a[N];
int r[N];
int ans[M];
bool vis[M];

int main() {
	n = read() , m = read();
	segt.root = segt.build(1 , n);
	for(int i = 1 ; i <= n ; i++)
		a[i] = read();
	for(int i = 1 ; i <= m ; i++)
		q[i].l = read() + 1 , q[i].r = read() + 1 , q[i].id = i;
	
	sort(q + 1 , q + m + 1 , cmp);
	Discretize(a + 1 , a + n + 1);
	
	for(int i = 1 , p = 0 ; i <= n ; i++) {
		while(p < n && vis[a[p + 1]] == false)
			vis[a[p + 1]] = true , ++p;
		r[i] = p;
		vis[a[i]] = false;
	}
	for(int i = 1 , p = 0 ; i <= m ; i++) {
		while(p <= n && r[p + 1] <= q[i].r)
			++p , segt.change2(segt.root , p , r[p] - p + 1);
			
		segt.change(segt.root , p + 1 , n , q[i].r - q[i - 1].r);
		ans[q[i].id] = segt.ask(segt.root , q[i].l , q[i].r);
	}
	
	for(int i = 1 ; i <= m ; i++)
		printf("%d
" , ans[i]);
	return 0;
}

---

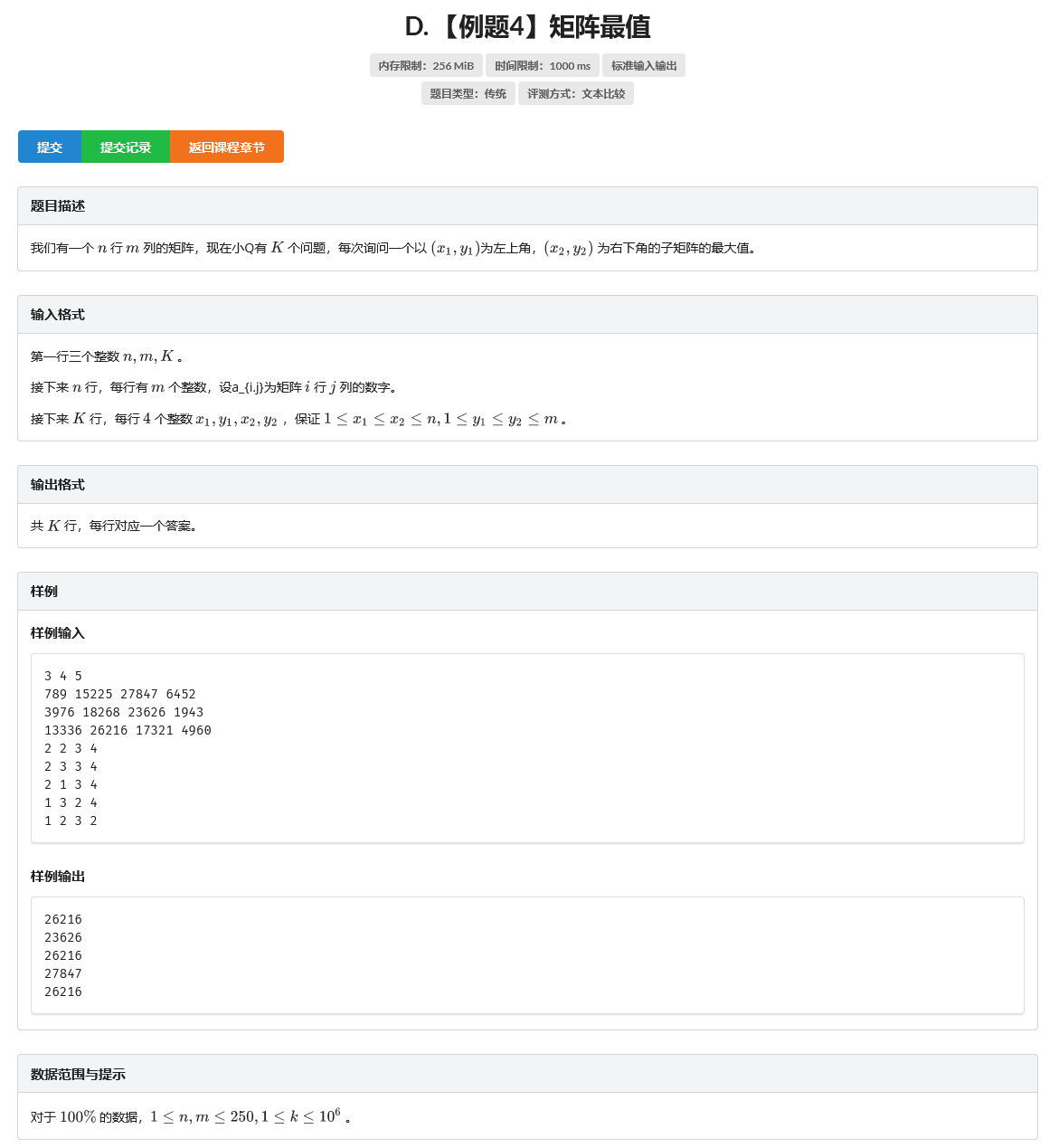
D. 【例题4】矩阵最值

题目

思路

二维ST表,没啥好说的,就是初始化的时候会不同,稍微理解下即可

code

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#define N 300
#define inf (int)0x80000000
using namespace std;
int read() {
	int re = 0;
	char c = getchar();
	bool sig = false;
	while(c < '0' || c > '9') {
		if(c == '-')	sig = true;
		c = getchar();
	}
	while(c >= '0' && c <= '9')
		re  = (re << 1) + (re << 3) + c - '0' , c = getchar();
	return sig ? -re : re;
}
int maxx(int a , int b , int c , int d) {
	return (a > b ? a : b) > (c > d ? c : d) ? (a > b ? a : b) : (c > d ? c : d);
}
#define max_(_ , __) ((_) > (__) ? (_) : (__))
int n , m , q;
int st[N * 2][N * 2][10][10];
int main() {
	memset(st , -0x3f , sizeof(st));
	n = read() , m = read() , q = read();
	for(int i = 1 ; i <= n ; i++)
		for(int j = 1 ; j <= m ; j++)
			st[i][j][0][0] = read();
	for(int I = 0 ; (1 << I) <= n ; I++)
		for(int J = 0 ; (1 << J) <= m ; J++) {
			if(I == 0 && J == 0)	continue;
			for(int i = 1 ; i <= n ; i++)
				for(int j = 1 ; j <= m ; j++)
					st[i][j][I][J] = (I != 0 ?
					max_(st[i][j][I - 1][J] , st[i + (1 << I - 1)][j][I - 1][J]) :
					max_(st[i][j][I][J - 1] , st[i][j + (1 << J - 1)][I][J - 1]) );
		}
	for(int i = 1 ; i <= q ; i++) {
		int lx , rx , ly , ry;
		lx = read() , ly = read() , rx = read() , ry = read();
		int kx = log(rx - lx + 1) / log(2);
		int ky = log(ry - ly + 1) / log(2);
		printf("%d
" , maxx(
		st[lx][ly][kx][ky] ,
		st[rx - (1 << kx) + 1][ly][kx][ky] , 
		st[lx][ry - (1 << ky) + 1][kx][ky] , 
		st[rx - (1 << kx) + 1][ry - (1 << ky) + 1][kx][ky]
		));
	}
	return 0;
}