链接
思路
我们希望x所在的连通块尽量的大,而且尽量走高处
离线的话可以询问排序,kruskal过程中更新答案
在线就要用kruskal重构树
这kruskal重构树的话,看图就明白了
叶子节点都是原树节点
非叶子节点都是边
按照从大到小的顺序依次加边(是深度不是长度)
如果连通块已经在一起就不联通,其他两个最大节点和这个边(新建节点)连边
看图就是很明白
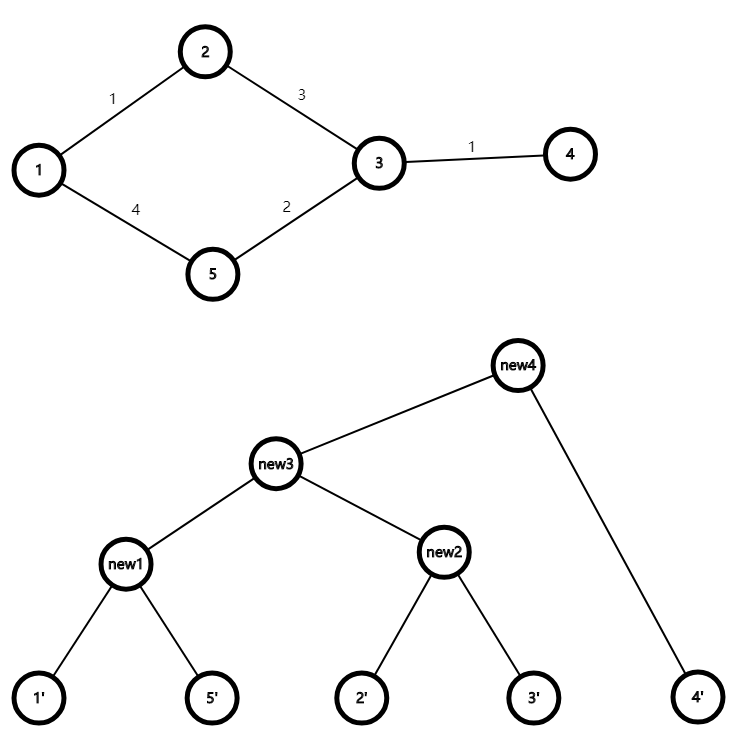
我们发现,重构树的根到任意节点是单调的,也就是说,这是个二叉堆啊
那两点间联通的最小需要深度就是lca(x,y)这条边的深度
询问就是s这个点最远能向上跳到的最远点的子树答案
可能我讲的听不懂,那就看图自己想想吧
复杂度最多一个log
大体流程
多组数据,进入solve
dij预处理dis
kruskal利用并查集重构出树来
lca树剖预处理重构树
再dfs统计子树ans
之后在线查询lca
输出lca这个点的ans
细节
并查集最好优化下,因为他重构出来的树很容易感觉成哈夫曼树的形状
并查集按秩合并和随机rand时间差别不大
树剖链外跳,链内二分
错误
写了比较慢、、(不过一遍60TLE还是很嗨的)
错误只有一个,dij的堆忘记了默认大顶堆,导致复杂度不对,T死了
代码
/*
大体流程:
多组数据,进入solve
dij预处理dis
kruskal重构出树来
lca树剖预处理重构树(其实就是二分)
再dfs统计子树ans
之后在线查询
*/
#include <iostream>
#include <ctime>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <queue>
#include <utility>
#include <algorithm>
using namespace std;
const int N=1e6+7;
int read() {
int x=0,f=1;char s=getchar();
for(;s>'9'||s<'0';s=getchar()) if(s=='-') f=-1;
for(;s>='0'&&s<='9';s=getchar()) x=x*10+s-'0';
return x*f;
}
int n,m,rt;
int dis[N],w[N<<1],dsr[N<<1];
struct node {
int u,v,l,a;
bool operator < (const node &b) const {
return a>b.a;
}
} edge[N];
struct noi_2018_t1 {
int v,nxt;
} e[N<<1];
int head[N<<1],add_tot;
void add(int u,int v) {
// cout<<u<<" "<<v<<"
";
e[++add_tot].v=v;
e[add_tot].nxt=head[u];
head[u]=add_tot;
}
namespace bcj {
int fa[N<<1],siz[N<<1],id[N<<1];
int find(int x) {
return fa[x]==x ? x : fa[x]=find(fa[x]);
}
void uu(int fx,int fy) {
fx=find(fx),fy=find(fy);
id[fx]=id[fy]=max(id[fx],id[fy]);
if(siz[fx]<=siz[fy]) {
fa[fx]=fy;
if(siz[fx]==siz[fy]) siz[fy]++;
} else {
fa[fy]=fx;
}
}
}
namespace get_lca {
int fa[N<<1],top[N<<1],siz[N<<1],son[N<<1],dep[N<<1],idx[N<<1],js,frm[N<<1];
void dfs1(int u,int f) {
dep[u]=dep[f]+1;
fa[u]=f;
siz[u]=1;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
dfs1(v,u);
siz[u]+=siz[v];
if(siz[son[u]]<siz[v]) son[u]=v;
}
}
void dfs2(int u,int topf) {
top[u]=topf;
idx[u]=++js;
frm[js]=u;
if(!son[u]) return;
dfs2(son[u],topf);
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(!idx[v]) dfs2(v,v);
}
}
int lca(int x,int val) {
int ans=x;
while(w[top[x]]>val) ans=top[x],x=fa[top[x]];
int l=idx[top[x]],r=idx[x];
while(l<=r) {
// cout<<l<<" "<<r<<"
";
int mid=(l+r)>>1;
if(w[frm[mid]]>val) ans=frm[mid],r=mid-1;
else l=mid+1;
}
return ans;
}
void init() {
dfs1(rt,0);
dfs2(rt,rt);
}
}
namespace dij {
struct node {
int v,nxt,q;
}e[N<<1];
int head[N<<1],tot;
void add(int u,int v,int q) {
e[++tot].v=v;
e[tot].q=q;
e[tot].nxt=head[u];
head[u]=tot;
}
void dij() {
priority_queue<pair<int,int> > q;
q.push(make_pair(0,1));
dis[1]=0;
while(!q.empty()) {
pair<int,int> u=q.top();
q.pop();
if(dis[u.second]!=-u.first) continue;
for(int i=head[u.second];i;i=e[i].nxt) {
int v=e[i].v;
if(dis[v]>dis[u.second]+e[i].q) {
dis[v]=dis[u.second]+e[i].q;
q.push(make_pair(-dis[v],v));
}
}
}
}
void work() {
memset(dis,0x3f,sizeof(dis));
memset(head,0,sizeof(head));
tot=0;
for(int i=1;i<=m;++i) {
add(edge[i].u,edge[i].v,edge[i].l);
add(edge[i].v,edge[i].u,edge[i].l);
}
dij();
}
}
namespace kruskal {
void work() {
for(int i=1;i<n+n;++i) bcj::fa[i]=i;
for(int i=1;i<n+n;++i) bcj::id[i]=i;
sort(edge+1,edge+1+m);
for(int i=1;i<=n;++i) w[i]=0x3f3f3f3f;
for(int i=1,js=n;i<=m;++i) {
int fx=bcj::find(edge[i].u),fy=bcj::find(edge[i].v);
if(fx!=fy) {
rt=++js;
add(js,bcj::id[fx]),add(js,bcj::id[fy]);
w[js]=edge[i].a;
bcj::uu(js,fy);
bcj::uu(js,fx);
if(js==n+n-1) return;
}
}
}
}
void clear() {
add_tot=0;
dij::tot=0;
get_lca::js=0;
memset(dij::head,0,sizeof(dij::head));
memset(get_lca::siz,0,sizeof(get_lca::siz));
memset(bcj::siz,0,sizeof(bcj::siz));
memset(head,0,sizeof(head));
memset(dis,0x3f,sizeof(dis));
memset(get_lca::idx,0,sizeof(get_lca::idx));
memset(get_lca::son,0,sizeof(get_lca::son));
}
void dfs(int u,int f) {
dsr[u]=dis[u];
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
dfs(v,u);
dsr[u]=min(dsr[u],dsr[v]);
}
}
void solve() {
dij::work();
// cout<<"1
";
kruskal::work();
// cout<<"2
";
get_lca::init();
// cout<<"3
";
dfs(rt,0);
int Q=read(),k=read();
int S=read(),lastans=0;
while(Q--) {
int vv=read(),pp=read();
int v=(vv+k*lastans-1)%n+1;
int p=(pp+k*lastans)%(S+1);
int tmp=get_lca::lca(v,p);
lastans=dsr[tmp];
printf("%d
",lastans);
}
}
int main() {
freopen("return.in","r",stdin);
freopen("return.out","w",stdout);
int T=read();
while(T--) {
n=read(),m=read();
for(int i=1;i<=m;++i) {
edge[i].u=read(),edge[i].v=read();
edge[i].l=read(),edge[i].a=read();
}
clear();
solve();
}
return 0;
}