FFT 快速傅里叶变换 学习笔记

FFT 快速傅里叶变换

前言

lmc,ikka,attack等众多大佬都没教会的我终于要自己填坑了。
又是机房里最后一个学fft的人

用处

多项式乘法

卷积

(g(x)=a_0+a_1x+a_2x^2)
(f(x)=b_0+b_1x+b_2x^2)
他们的乘积c(x)就是
(c(x)=a_0b_0+a_0b_1x+a_0b_2x^2+a_1b_0x+a_1b_1x^2+a_1b_2x^3+a_2b_0x^2+a_2b_1x^3+a_2b_2x^4)
c(x)叫做g(x)和f(x)的卷积
就是定义了一个多项式的乘法操作
(O(n^2))这样子写（还是代码明了）

    n=read(),m=read();
	for(int i=0;i<=n;++i) a[i]=read();
	for(int i=0;i<=m;++i) b[i]=read();
	for(int i=0;i<=n;++i)	
		for(int j=0;j<=m;++j)
			c[i+j]+=a[i]*b[j];
	for(int i=0;i<=n+m;++i) printf("%d ",c[i]);

0x01

太慢了！！！
所以我们要用FFT进行优化，复杂度会降为(O(nlogn))

多项式表示法

我们常用的是系数表示法，就是上文中用到的。
(f(x)=a_0+a_1x+a_2x^2)
现在我们学习新的表示法，点值法。
顾名思义，就是{x,f(x)}，然后我们只需要n+1的不同组就可以唯一确定一个多项式f(x)了，想一下高斯消元。

一些定义

多项式由系数表示法转为点值表示法的过程，就成为DFT。
相对地，把一个多项式的点值表示法转化为系数表示法的过程，就是IDFT。
而FFT就是通过取某些特殊的x的点值来加速DFT和IDFT的过程。

复数的定义及其运算

复数由实数和虚数组成
虚数可以表示为i*x,其中(i=sqrt{-1})
复数的表示形式有四种。
代数形式：(z=a+bi,a,bin R)
几何形式：代数形式与复平面上的点((a,b))或者向量(vec{OZ})一一对应
三角形式：(z=r(cos heta+isin heta)，rgeq0, hetain R)
指数形式：(z=re^{i heta}，rgeq0, hetain R)

何为复平面，就是笛卡尔坐标系，横轴为实数，纵轴为虚数。
欧拉公式：(e^{i heta}=cos heta+isin heta)
r为模长（长度），( heta)为辅角(角度)

乘法

((a+bi)(c+di)=(ac-bd)+(bc+ad)i)
长度相乘，角度相加
((r_1, heta_1)*(r_2, heta_2)=(r_1r_2, heta_1 heta_2))

单位根

一个n等分的单位圆
上面每一份的那个点为(w_n^i)
attack的图真好看

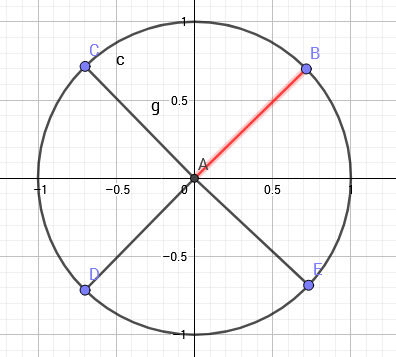
至于为何要扯复数单位根，就是因为它有一些美妙的性质可以降低我们的复杂度。

性质1

(w_n^k=w_{2n}^{2k})

性质2

(w_n^{2k}=-w_n^k)

性质3

(w_n^n=1)或者(w_n^{kn+m}=w_n^{m})
这些性质都可以套用欧拉公式((e^{i heta}=cos heta+isin heta))证明
或者 {
1、表示的都是一个点。
2、关于原点对称。
3.显然，或者说以n为循环节
}

FFT

分治！！
(f(x)=a_0+a_1x+a_2x^2)
n为偶数
把它按照奇偶分成两个等幂的多项式。
(f(x)=a_0+a_1x+a_2x^2+a_3x^3)
设(a(x)=a_0+a_2x)，(b(x)=a_1+a_3x)
那么(f(x)=a(x^2)+xb(x^2))
我们依次带入(w_n^k),算出来(f(w_n^k))，复杂度依旧O(n^2)
但是我们还有性质没用
假设(k<frac{n}{2})，现在要把(x=ω_k^n)代入f(x)
(f(x)=a((w_n^k)^2)+w_n^kb((w_n^k)^2))
(f(x)=a(w_n^{2k})+w_n^kb(w_n^{2k}))
(f(x)=a(w_{frac{n}{2}}^{k})+w_n^kb(w_{frac{n}{2}}^{k}))
我们再带入(w_n^{k+frac{n}{2}})试试
(f(x)=a((w_n^{k+frac{n}{2}})^2)+w_n^{k+frac{n}{2}}b((w_n^{k+frac{n}{2}})^2))
(f(x)=a(w_n^{2k+n})+w_n^{k+frac{n}{2}}b(w_n^{2k+n}))
(f(x)=a(w_n^{2k})-w_n^{k}b(w_n^{2k}))
(f(x)=a(w_{frac{n}{2}}^{k})-w_n^kb(w_{frac{n}{2}}^{k}))
我们求出1的时候就可以顺带求出2来了。

IFFT

一个多项式在分治的过程中乘上单位根的共轭复数，分治完的每一项除以n即为原多项式的每一项系数.

意思就是说FFT和IFFT可以一起搞.
不明白，留坑

具体

递归版fft好像一班都不写，需要蝴蝶效应，二进制什么的的优化成非递归版。

代码

#include <bits/stdc++.h>
using namespace std;
const int N=4e6+7;
const double Pi=acos(-1.0);
int read() {
	int x=0,f=1;char s=getchar();
	for(;s>'9'||s<'0';s=getchar()) if(s=='-') f=-1;
	for(;s>='0'&&s<='9';s=getchar()) x=x*10+s-'0';
	return x*f;
}
int n,m,r[N],limit=1;
struct Complex {
	double x,y;
	Complex(double xx=0,double yy=0) {x=xx,y=yy;}
}a[N],b[N];
Complex operator + (Complex a,Complex b) {return Complex(a.x+b.x,a.y+b.y);}
Complex operator - (Complex a,Complex b) {return Complex(a.x-b.x,a.y-b.y);}
Complex operator * (Complex a,Complex b) {return Complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
void fft(Complex *a,int type) {
	for(int i=0;i<=limit;++i)
		if(i<r[i]) swap(a[i],a[r[i]]);
	for(int mid=1;mid<limit;mid<<=1) {
		Complex Wn(cos(Pi/mid),type*sin(Pi/mid));
		for(int R=mid<<1,j=0;j<limit;j+=R) {
			Complex w(1,0);
			for(int k=0;k<mid;++k,w=w*Wn) {
				Complex x=a[j+k],y=w*a[j+mid+k];
				a[j+k]=x+y;
				a[j+k+mid]=x-y;	
			}
		}
	}
}
int main() {
	n=read(),m=read();
	for(int i=0;i<=n;++i) a[i].x=read();
	for(int i=0;i<=m;++i) b[i].x=read();
	int l=0;while(limit<=n+m) limit<<=1,l++;
	for(int i=0;i<=limit;++i)
		r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
	fft(a,1),fft(b,1);
	for(int i=0;i<=limit;++i) a[i]=a[i]*b[i];
	fft(a,-1);
	for(int i=0;i<=n+m;++i) printf("%d ",(int)(a[i].x/limit+0.5));
	return 0;
}

参考||引用

鸣谢
zhihu大佬
路人黑的纸巾
胡小兔
attack