一点线性筛的东西

目录

• 线性筛
  • 求莫比乌斯函数
  • 求欧拉函数
  • 约数个数
  • 约数和

线性筛

(csp)还有不到一个月。
才发现自己不会线性筛，(mdzz).
(代码都没试过，请谨慎使用)

for(int i=2;i<=n;++i) {
	if(!vis[i]) pri[++cnt]=i;
	for(int j=1;j<=cnt&&i*pri[j]<=n;++j) {
		vis[i*pri[j]]=1;
		if(i%pri[j]==0) break;
	}
}

只会被最小的素数筛掉。
(n=p_1^{k_1}*p_2^{k_2}……p_x^{k_x})
枚举的(i)为(frac{n}{p_1})
当(n\%pri[j]==0) 就是说枚举到了(pri[j]*i)的最小质因子的边界了。
再往后的(pri[j])就会比(i)里面的质因子小了，当然不行了。
之前的质因子都是小于(i)的质因子，当然行了。
(n\%pri[j]==0)就是恰好相等的时候。
可以很方便的求积性函数，只需要毒瘤的简单的分类讨论就好了。

求莫比乌斯函数

[ mu(x)=left{ egin{aligned} & 1& n=1 \ & (-1)^k& n=p_1*p_2…p_k \ & 0& n=others end{aligned} ight. ]

mu[1]=1;
for(int i=2;i<=n;++i) {
	if(!vis[i]) {
		pri[++cnt]=i;
		mu[i]=-1;
	}
	for(int j=1;j<=cnt&&i*pri[j]<=n;++j) {
		vis[i*pri[j]]=1;
		if(i%pri[j]==0) {
			mu[i*pri[j]]=0;
			break;
		} else mu[i*pri[j]]=-mu[i];
	}
}

那些

[ sum_{d|n}mu(d)=left{ egin{aligned} & 1& n=1 \ & 0& n>1 end{aligned} ight. ]

这个二项式定理啥的证
(sum_{i=0}^{k}(-1)^kC_k^i).

求欧拉函数

(phi(n))与(n)互质的数的个数
之前写的懒得敲了。



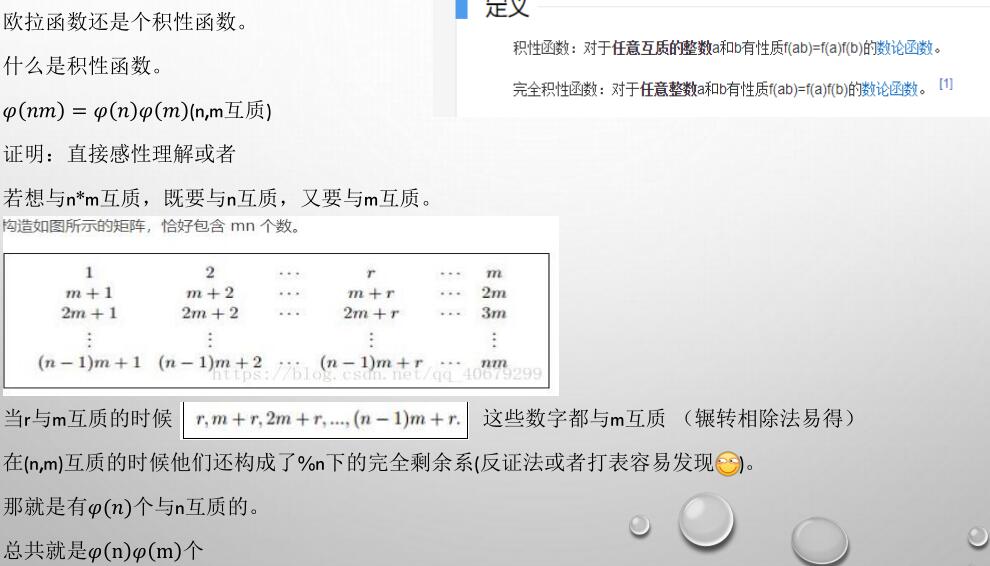
筛的主要还是利用(n*frac{p_1-1}{p_1}……frac{p_k-1}{p_k})

phi[1]=1;
for(int i=2;i<=n;++i) {
	if(!vis[i]) {
		pri[++cnt]=i;
		phi[i]=i-1;
	}
	for(int j=1;j<=cnt&&i*pri[j]<=n;++j) {
		vis[i*pri[j]]=1;
		if(i%pri[j]==0) {
			phi[i*pri[j]]=phi[i]*pri[j];
			break;
		} else phi[i*pri[j]]=phi[i]*(pri[j]-1);
	}
}

[sum_{d|n}phi(d)=n ]

咱不会证，咱也不想想.

约数个数

如果 (x=p_1^{c_1}p_2^{c_2}...p_k^{c_k}) ，则 (d(x)=(1+c_1)(1+c_2)...(1+c_k))
筛的过程中，我们记录一个 (num(x)) 表示 (x) 的最小质因子的个数，即 (c_1) 。
然后(xjb)转移

for(int i=2;i<=n;++i) {
	if(!vis[i]) {
		pri[++cnt]=i;
		num[i]=1;
		d[i]=2;
	}
	for(int j=1;j<=cnt&&i*pri[j]<=n;++j) {
		vis[i*pri[j]]=1;
		if(i%pri[j]==0) {
			num[i*pri[j]]=num[i]+1;
			d[i*pri[j]]=d[i]/(num[i]+1)*(num[i*pri[j]]+1);
			break;
		} else {
			num[i*pri[j]]=1;
			d[i*pri[j]]=d[i]*2;
		}
	}
}

约数和

我们设sd(i)表示i的约数和。
(sd(n)=(1+p_1+…+p_1^{r_1})*(1+p_2+…+p_2^{r_2})*…*(1+p_k…+p_k^{r_k}))
等差数列似的一个东西。
这个时候我们需要记录最小质因子的那一项也就是((1+p_x+p_x^2+……+p_x^{r_1}))，叫他(num(i)).可以设sd(i)表示i的约数和。设
(一)，当前数是一个素数：
(sd(i)=i+1)
(num(i)=i+1)
(二)，当前数取模枚举的质数不等于0
​((i*prime[j]))里原先没有((prime[j]))这一项，加上这一项之后可得：(sd(i*prime[j])=sd(i)*sd(prime[j]))
(num(i*prime[j])=1+prime[j])
(三)，当前数取模枚举的质数等于0
(sd(i*prime[j])=sd(i)/num(i)*(num(i)*prime[j]+1))
(num(i*prime[j])=num(i)*prime[j]+1)

sd[1]=1;
for(int i=2;i<=n;++i) {
	if(!vis[i]) {
		pri[++cnt]=i;
		num[i]=sd[i]=i+1;
	}
	for(int j=1;j<=cnt&&i*pri[j]<=n;++j) {
		vis[i*pri[j]]=1;
		if(i%pri[j]==0) {
			sd[i*pri[j]]=sd[i]/num[i]*(num[i]*pri[j]+1);
			num[i*pri[j]]=num[i]*pri[j]+1;
			break;
		} else {
			sd[i*pri[j]]=sd[i]*sd[pri[j]];
			num[i*pri[j]]=pri[j]+1;
		}
	}
}