Java各种排序算法详解
排序大的分类可以分为两种:内排序和外排序。在排序过程中,全部记录存放在内存,则称为内排序,如果排序过程中需要使用外存,则称为外排序。下面讲的排序都是属于内排序。
内排序有可以分为以下几类:
(1)、插入排序:直接插入排序、二分法插入排序、希尔排序。
(2)、选择排序:简单选择排序、堆排序。
(3)、交换排序:冒泡排序、快速排序。
(4)、归并排序
(5)、基数排序
一、插入排序
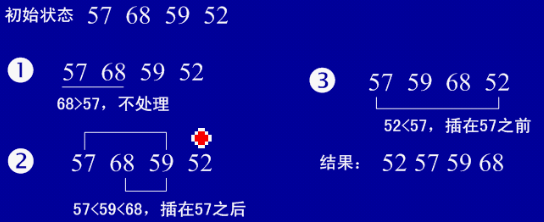
①插入排序(从后向前找到合适位置后插入)
1、基本思想:每步将一个待排序的记录,按其顺序码大小插入到前面已经排序的字序列的合适位置(从后向前找到合适位置后),直到全部插入排序完为止。
2、实例
3、java实现
实现一:
1 package com.sort;
2
3 public class 直接插入排序 {
4
5 public static void main(String[] args) {
6 int[] a={49,38,65,97,76,13,27,49,78,34,12,64,1};
7 System.out.println("排序之前:");
8 for (int i = 0; i < a.length; i++) {
9 System.out.print(a[i]+" ");
10 }
11 //直接插入排序
12 for (int i = 1; i < a.length; i++) {
13 //待插入元素
14 int temp = a[i];
15 int j;
16 /*for (j = i-1; j>=0 && a[j]>temp; j--) {
17 //将大于temp的往后移动一位
18 a[j+1] = a[j];
19 }*/
20 for (j = i-1; j>=0; j--) {
21 //将大于temp的往后移动一位
22 if(a[j]>temp){
23 a[j+1] = a[j];
24 }else{
25 break;
26 }
27 }
28 a[j+1] = temp;
29 }
30 System.out.println();
31 System.out.println("排序之后:");
32 for (int i = 0; i < a.length; i++) {
33 System.out.print(a[i]+" ");
34 }
35 }
36
37 }
实现二:
public class ChaRu {
public static void anChaRu(int[] arr) {
if (arr == null || arr.length == 0)
return;
for (int i = 1; i < arr.length; i++) {// 假设第一个数的位置是正确的,要想往后移,就必须要假设第一个数的位置是正确的。
int j = i;
int target = arr[i];// 等待插入数字
// 后移数字
while (j > 0 && target < arr[j - 1]) {
arr[j] = arr[j - 1];
j--;
}
// 插入数字
arr[j] = target;
}
}
}
4、分析
直接插入排序是稳定的排序。关于各种算法的稳定性分析可以参考http://www.cnblogs.com/Braveliu/archive/2013/01/15/2861201.html
文件初态不同时,直接插入排序所耗费的时间有很大差异。若文件初态为正序,则每个待插入的记录只需要比较一次就能够找到合适的位置插入,故算法的时间复杂度为O(n),这时最好的情况。若初态为反序,则第i个待插入记录需要比较i+1次才能找到合适位置插入,故时间复杂度为O(n2),这时最坏的情况。
直接插入排序的平均时间复杂度为O(n2)。
②二分法插入排序(按二分法找到合适位置插入)
1、基本思想:二分法插入排序的思想和直接插入一样,只是找合适的插入位置的方式不同,这里是按二分法找到合适的位置,可以减少比较的次数。
2、实例

3、java实现
1 package com.sort;
2
3 public class 二分插入排序 {
4 public static void main(String[] args) {
5 int[] a={49,38,65,97,176,213,227,49,78,34,12,164,11,18,1};
6 System.out.println("排序之前:");
7 for (int i = 0; i < a.length; i++) {
8 System.out.print(a[i]+" ");
9 }
10 //二分插入排序
11 sort(a);
12 System.out.println();
13 System.out.println("排序之后:");
14 for (int i = 0; i < a.length; i++) {
15 System.out.print(a[i]+" ");
16 }
17 }
18
19 private static void sort(int[] a) {
20 for (int i = 0; i < a.length; i++) {
21 int temp = a[i];
22 int left = 0;
23 int right = i-1;
24 int mid = 0;
25 while(left<=right){
26 mid = (left+right)/2;
27 if(temp<a[mid]){
28 right = mid-1;
29 }else{
30 left = mid+1;
31 }
32 }
33 for (int j = i-1; j >= left; j--) {
34 a[j+1] = a[j];
35 }
36 if(left != i){
37 a[left] = temp;
38 }
39 }
40 }
41 }
4、分析
当然,二分法插入排序也是稳定的。
二分插入排序的比较次数与待排序记录的初始状态无关,仅依赖于记录的个数。当n较大时,比直接插入排序的最大比较次数少得多。但大于直接插入排序的最小比较次数。算法的移动次数与直接插入排序算法的相同,最坏的情况为n2/2,最好的情况为n,平均移动次数为O(n2)。
③希尔排序
1、基本思想:先取一个小于n的整数d1作为第一个增量,把文件的全部记录分成d1个组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量d2<d1重复上述的分组和排序,直至所取的增量dt=1(dt<dt-l<…<d2<d1),即所有记录放在同一组中进行直接插入排序为止。该方法实质上是一种分组插入方法。
2、实例

3、java实现
实现一:
1 package com.sort;
2
3 //不稳定
4 public class 希尔排序 {
5
6
7 public static void main(String[] args) {
8 int[] a={49,38,65,97,76,13,27,49,78,34,12,64,1};
9 System.out.println("排序之前:");
10 for (int i = 0; i < a.length; i++) {
11 System.out.print(a[i]+" ");
12 }
13 //希尔排序
14 int d = a.length;
15 while(true){
16 d = d / 2;
17 for(int x=0;x<d;x++){
18 for(int i=x+d;i<a.length;i=i+d){
19 int temp = a[i];
20 int j;
21 for(j=i-d;j>=0&&a[j]>temp;j=j-d){
22 a[j+d] = a[j];
23 }
24 a[j+d] = temp;
25 }
26 }
27 if(d == 1){
28 break;
29 }
30 }
31 System.out.println();
32 System.out.println("排序之后:");
33 for (int i = 0; i < a.length; i++) {
34 System.out.print(a[i]+" ");
35 }
36 }
37
38 }
实现二:
public class XiEr {
/*
* 希尔排序的一趟插入
*
* @param arr 待排序数组
*
* @param d 增量
*/
public static void shellInsert(int[] arr, int d) {
for (int i = d; i < arr.length; i++) {
int j = i - d;
int temp = arr[i];// 记录要插入的数据
while (j >= 0 && arr[j] > temp) {// 从后向前,找到比其小的数的位置
arr[j + d] = arr[j];// 向后挪动
j -= d;
}
if (j != i - d)// 存在比其小的数
arr[j + d] = temp;
}
}
public static void shellSort(int[] arr) {
if (arr == null || arr.length == 0)
return;
int d = arr.length / 2;
while (d >= 1) {
shellInsert(arr, d);
d /= 2;
}
}
}
4、分析
我们知道一次插入排序是稳定的,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以希尔排序是不稳定的。
希尔排序的时间性能优于直接插入排序,原因如下:
二、选择排序

1 package com.sort;
2
3 //不稳定
4 public class 简单的选择排序 {
5
6 public static void main(String[] args) {
7 int[] a={49,38,65,97,76,13,27,49,78,34,12,64,1,8};
8 System.out.println("排序之前:");
9 for (int i = 0; i < a.length; i++) {
10 System.out.print(a[i]+" ");
11 }
12 //简单的选择排序
13 for (int i = 0; i < a.length; i++) {
14 int min = a[i];
15 int n=i; //最小数的索引
16 for(int j=i+1;j<a.length;j++){
17 if(a[j]<min){ //找出最小的数
18 min = a[j];
19 n = j;
20 }
21 }
22 a[n] = a[i];
23 a[i] = min;
24
25 }
26 System.out.println();
27 System.out.println("排序之后:");
28 for (int i = 0; i < a.length; i++) {
29 System.out.print(a[i]+" ");
30 }
31 }
32
33 }
实现二:
public class XuanZe {
public static void anXuanZe(int[] arr) {
if (arr == null || arr.length == 0)
return;
int minIndex = 0;
for (int i = 0; i < arr.length - 1; i++) { // 只需要比较n-1次。
minIndex = i;
for (int j = i + 1; j < arr.length; j++) { // 从i+1开始比较,因为minIndex默认为i,所以i就不用再比较了。
if (arr[j] < arr[minIndex])
minIndex = j;
if (minIndex != i) // 如果minIndex不是i,说明找到了最小的值,交换之。
swap(arr, i, minIndex);
}
}
}
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
4、分析
简单选择排序是不稳定的排序。
时间复杂度:T(n)=O(n2)。
②堆排序
1、基本思想:
堆排序是一种树形选择排序,是对直接选择排序的有效改进。
堆的定义:具有n个元素的序列 (h1,h2,...,hn),当且仅当满足(hi>=h2i,hi>=2i+1)或(hi<=h2i,hi<=2i+1) (i=1,2,...,n/2)时称之为堆。在这里只讨论满足前者条件的堆。由堆的定义可以看出,堆顶元素(即第一个元素)必为最大项(大顶堆)。完全二 叉树可以很直观地表示堆的结构。堆顶为根,其它为左子树、右子树。
思想:初始时把要排序的数的序列看作是一棵顺序存储的二叉树,调整它们的存储序,使之成为一个 堆,这时堆的根节点的数最大。然后将根节点与堆的最后一个节点交换。然后对前面(n-1)个数重新调整使之成为堆。依此类推,直到只有两个节点的堆,并对 它们作交换,最后得到有n个节点的有序序列。从算法描述来看,堆排序需要两个过程,一是建立堆,二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆的渗透函数,二是反复调用渗透函数实现排序的函数。
2、实例
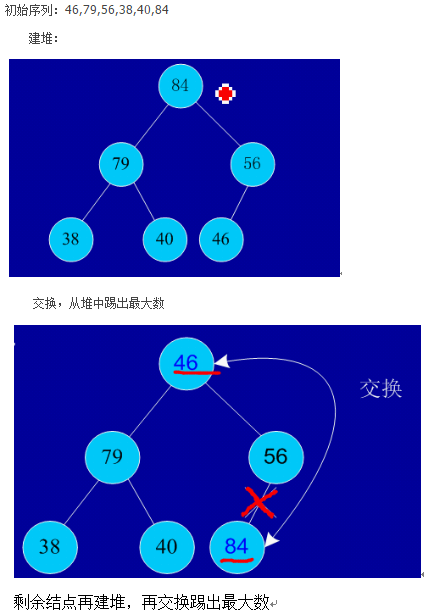
依次类推:最后堆中剩余的最后两个结点交换,踢出一个,排序完成。
3、java实现
1 package com.sort;
2 //不稳定
3 import java.util.Arrays;
4
5 public class HeapSort {
6 public static void main(String[] args) {
7 int[] a={49,38,65,97,76,13,27,49,78,34,12,64};
8 int arrayLength=a.length;
9 //循环建堆
10 for(int i=0;i<arrayLength-1;i++){
11 //建堆
12 buildMaxHeap(a,arrayLength-1-i);
13 //交换堆顶和最后一个元素
14 swap(a,0,arrayLength-1-i);
15 System.out.println(Arrays.toString(a));
16 }
17 }
18 //对data数组从0到lastIndex建大顶堆
19 public static void buildMaxHeap(int[] data, int lastIndex){
20 //从lastIndex处节点(最后一个节点)的父节点开始
21 for(int i=(lastIndex-1)/2;i>=0;i--){
22 //k保存正在判断的节点
23 int k=i;
24 //如果当前k节点的子节点存在
25 while(k*2+1<=lastIndex){
26 //k节点的左子节点的索引
27 int biggerIndex=2*k+1;
28 //如果biggerIndex小于lastIndex,即biggerIndex+1代表的k节点的右子节点存在
29 if(biggerIndex<lastIndex){
30 //若果右子节点的值较大
31 if(data[biggerIndex]<data[biggerIndex+1]){
32 //biggerIndex总是记录较大子节点的索引
33 biggerIndex++;
34 }
35 }
36 //如果k节点的值小于其较大的子节点的值
37 if(data[k]<data[biggerIndex]){
38 //交换他们
39 swap(data,k,biggerIndex);
40 //将biggerIndex赋予k,开始while循环的下一次循环,重新保证k节点的值大于其左右子节点的值
41 k=biggerIndex;
42 }else{
43 break;
44 }
45 }
46 }
47 }
48 //交换
49 private static void swap(int[] data, int i, int j) {
50 int tmp=data[i];
51 data[i]=data[j];
52 data[j]=tmp;
53 }
54 }
4、分析
堆排序也是一种不稳定的排序算法。
堆排序优于简单选择排序的原因:
直接选择排序中,为了从R[1..n]中选出关键字最小的记录,必须进行n-1次比较,然后在R[2..n]中选出关键字最小的记录,又需要做n-2次比较。事实上,后面的n-2次比较中,有许多比较可能在前面的n-1次比较中已经做过,但由于前一趟排序时未保留这些比较结果,所以后一趟排序时又重复执行了这些比较操作。
堆排序可通过树形结构保存部分比较结果,可减少比较次数。
堆排序的最坏时间复杂度为O(nlogn)。堆序的平均性能较接近于最坏性能。由于建初始堆所需的比较次数较多,所以堆排序不适宜于记录数较少的文件。
三、交换排序
①冒泡排序
1、基本思想:在要排序的一组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。即:每当两相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。
2、实例

3、java实现
实现一:
1 package com.sort;
2
3 //稳定
4 public class 冒泡排序 {
5 public static void main(String[] args) {
6 int[] a={49,38,65,97,76,13,27,49,78,34,12,64,1,8};
7 System.out.println("排序之前:");
8 for (int i = 0; i < a.length; i++) {
9 System.out.print(a[i]+" ");
10 }
11 //冒泡排序
12 for (int i = 0; i < a.length; i++) {
13 for(int j = 0; j<a.length-i-1; j++){
14 //这里-i主要是每遍历一次都把最大的i个数沉到最底下去了,没有必要再替换了
15 if(a[j]>a[j+1]){
16 int temp = a[j];
17 a[j] = a[j+1];
18 a[j+1] = temp;
19 }
20 }
21 }
22 System.out.println();
23 System.out.println("排序之后:");
24 for (int i = 0; i < a.length; i++) {
25 System.out.print(a[i]+" ");
26 }
27 }
28 }
实现二:
public class MaoPao {
public static void anMaoPao(int[] arr) {
if (arr == null || arr.length == 0)
return;
for (int i = 0; i < arr.length - 1; i++) {
for (int j = arr.length - 1; j > i; j--) {
if (arr[j] < arr[j - 1])
swap(arr, j - 1, j);
}
}
}
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
4、分析
冒泡排序是一种稳定的排序方法。

package com.sort;
//不稳定
public class 快速排序 {
public static void main(String[] args) {
int[] a={49,38,65,97,76,13,27,49,78,34,12,64,1,8};
System.out.println("排序之前:");
for (int i = 0; i < a.length; i++) {
System.out.print(a[i]+" ");
}
//快速排序
quick(a);
System.out.println();
System.out.println("排序之后:");
for (int i = 0; i < a.length; i++) {
System.out.print(a[i]+" ");
}
}
private static void quick(int[] a) {
if(a.length>0){
quickSort(a,0,a.length-1);
}
}
private static void quickSort(int[] a, int low, int high) {
if(low<high){ //如果不加这个判断递归会无法退出导致堆栈溢出异常
int middle = getMiddle(a,low,high);
quickSort(a, 0, middle-1);
quickSort(a, middle+1, high);
}
}
private static int getMiddle(int[] a, int low, int high) {
int temp = a[low];//基准元素
while(low<high){
//找到比基准元素小的元素位置
while(low<high && a[high]>=temp){
high--;
}
a[low] = a[high];
while(low<high && a[low]<=temp){
low++;
}
a[high] = a[low];
}
a[low] = temp;
return low;
}
}
实现二:
public class KuaiSu {
// 一次划分
public static int partition(int[] arr, int left, int right) {
int pivotKey = arr[left];
int pivotPointer = left;
while (left < right) {
while (left < right && arr[right] >= pivotKey)
right--;
while (left < right && arr[left] <= pivotKey)
left++;
swap(arr, left, right);// 把大的交换到右边,把小的交换到左边。
}
swap(arr, pivotPointer, left);// 最后把pivot交换到中间。
return left;
}
private static void swap(int[] arr, int left, int right) {
int temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
}
public static void quickSort(int[] arr, int left, int right) {
if (left >= right)
return;
int pivotPos = partition(arr, left, right);
quickSort(arr, left, pivotPos - 1);
quickSort(arr, pivotPos + 1, right);
}
public static void sort(int[] arr) {
if (arr == null || arr.length == 0)
return;
quickSort(arr, 0, arr.length - 1);
}
}
实现三:
//冒泡+二分+递归分治
public class KuaiSu2 {
/*
* 划分
*
* @param arr
*
* @param left
*
* @param right
*
* @return
*/
public static int partition(int[] arr, int left, int right) {
int pivotKey = arr[left];
while (left < right) {
while (left < right && arr[right] >= pivotKey)
right--;
arr[left] = arr[right];// 把小的移动到左边
while (left < right && arr[left] <= pivotKey)
left++;
arr[right] = arr[left];// 把大的移动到右边
}
arr[left] = pivotKey;// 最后把pivotKey赋值到中间
return left;
/*
* 递归划分子序列
*
* @param arr
*
* @param left
*
* @param right
*/
}
public static void quickSort(int[] arr, int left, int right) {
if (left >= right)
return;
int pivotPos = partition(arr, left, right);
quickSort(arr, pivotPos + 1, right);
}
public static void sort(int[] arr) {
if (arr == null || arr.length == 0)
return;
quickSort(arr, 0, arr.length);
}
}
4、分析
快速排序是不稳定的排序。
快速排序的时间复杂度为O(nlogn)。
当n较大时使用快排比较好,当序列基本有序时用快排反而不好。
四、归并排序
1、基本思想:归并(Merge)排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
2、实例

3、java实现
1 package com.sort;
2
3 //稳定
4 public class 归并排序 {
5 public static void main(String[] args) {
6 int[] a={49,38,65,97,76,13,27,49,78,34,12,64,1,8};
7 System.out.println("排序之前:");
8 for (int i = 0; i < a.length; i++) {
9 System.out.print(a[i]+" ");
10 }
11 //归并排序
12 mergeSort(a,0,a.length-1);
13 System.out.println();
14 System.out.println("排序之后:");
15 for (int i = 0; i < a.length; i++) {
16 System.out.print(a[i]+" ");
17 }
18 }
19
20 private static void mergeSort(int[] a, int left, int right) {
21 if(left<right){
22 int middle = (left+right)/2;
23 //对左边进行递归
24 mergeSort(a, left, middle);
25 //对右边进行递归
26 mergeSort(a, middle+1, right);
27 //合并
28 merge(a,left,middle,right);
29 }
30 }
31
32 private static void merge(int[] a, int left, int middle, int right) {
33 int[] tmpArr = new int[a.length];
34 int mid = middle+1; //右边的起始位置
35 int tmp = left;
36 int third = left;
37 while(left<=middle && mid<=right){
38 //从两个数组中选取较小的数放入中间数组
39 if(a[left]<=a[mid]){
40 tmpArr[third++] = a[left++];
41 }else{
42 tmpArr[third++] = a[mid++];
43 }
44 }
45 //将剩余的部分放入中间数组
46 while(left<=middle){
47 tmpArr[third++] = a[left++];
48 }
49 while(mid<=right){
50 tmpArr[third++] = a[mid++];
51 }
52 //将中间数组复制回原数组
53 while(tmp<=right){
54 a[tmp] = tmpArr[tmp++];
55 }
56 }
57 }
4、分析
归并排序是稳定的排序方法。
归并排序的时间复杂度为O(nlogn)。
速度仅次于快速排序,为稳定排序算法,一般用于对总体无序,但是各子项相对有序的数列。
五、基数排序
1、基本思想:将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
2、实例

3、java实现
1 package com.sort;
2
3 import java.util.ArrayList;
4 import java.util.List;
5 //稳定
6 public class 基数排序 {
7 public static void main(String[] args) {
8 int[] a={49,38,65,97,176,213,227,49,78,34,12,164,11,18,1};
9 System.out.println("排序之前:");
10 for (int i = 0; i < a.length; i++) {
11 System.out.print(a[i]+" ");
12 }
13 //基数排序
14 sort(a);
15 System.out.println();
16 System.out.println("排序之后:");
17 for (int i = 0; i < a.length; i++) {
18 System.out.print(a[i]+" ");
19 }
20 }
21
22 private static void sort(int[] array) {
23 //找到最大数,确定要排序几趟
24 int max = 0;
25 for (int i = 0; i < array.length; i++) {
26 if(max<array[i]){
27 max = array[i];
28 }
29 }
30 //判断位数
31 int times = 0;
32 while(max>0){
33 max = max/10;
34 times++;
35 }
36 //建立十个队列
37 List<ArrayList> queue = new ArrayList<ArrayList>();
38 for (int i = 0; i < 10; i++) {
39 ArrayList queue1 = new ArrayList();
40 queue.add(queue1);
41 }
42 //进行times次分配和收集
43 for (int i = 0; i < times; i++) {
44 //分配
45 for (int j = 0; j < array.length; j++) {
46 int x = array[j]%(int)Math.pow(10, i+1)/(int)Math.pow(10, i);
47 ArrayList queue2 = queue.get(x);
48 queue2.add(array[j]);
49 queue.set(x,queue2);
50 }
51 //收集
52 int count = 0;
53 for (int j = 0; j < 10; j++) {
54 while(queue.get(j).size()>0){
55 ArrayList<Integer> queue3 = queue.get(j);
56 array[count] = queue3.get(0);
57 queue3.remove(0);
58 count++;
59 }
60 }
61 }
62 }
63 }
4、分析
基数排序是稳定的排序算法。
基数排序的时间复杂度为O(d(n+r)),d为位数,r为基数。
测试类
以下是几种排序方法的测试类:
import java.util.Random;
/**
* 排序测试类
*
* 排序算法的分类如下: 1.插入排序(直接插入排序、折半插入排序、希尔排序); 2.交换排序(冒泡泡排序、快速排序);
* 3.选择排序(直接选择排序、堆排序); 4.归并排序; 5.基数排序。
*
* 关于排序方法的选择: (1)若n较小(如n≤50),可采用直接插入或直接选择排序。
* 当记录规模较小时,直接插入排序较好;否则因为直接选择移动的记录数少于直接插人,应选直接选择排序为宜。
* (2)若文件初始状态基本有序(指正序),则应选用直接插人、冒泡或随机的快速排序为宜;
* (3)若n较大,则应采用时间复杂度为O(nlgn)的排序方法:快速排序、堆排序或归并排序。
*
*/
public class SortTest {
/**
* 初始化测试数组的方法
*
* @return 一个初始化好的数组
*/
public int[] createArray() {
Random random = new Random();
int[] array = new int[10];
for (int i = 0; i < 10; i++) {
array[i] = random.nextInt(100) - random.nextInt(100);// 生成两个随机数相减,保证生成的数中有负数
}
System.out.print("原始序列:");
printArray(array);
return array;
}
/**
* 打印数组中的元素到控制台
*
* @param source
*/
public void printArray(int[] data) {
for (int i : data) {
System.out.print(i + " ");
}
System.out.println();
}
/**
* 交换数组中指定的两元素的位置
*
* @param data
* @param x
* @param y
*/
private void swap(int[] data, int x, int y) {
int temp = data[x];
data[x] = data[y];
data[y] = temp;
}
/**
* 冒泡排序----交换排序的一种
* 方法:相邻两元素进行比较,如有需要则进行交换,每完成一次循环就将最大元素排在最后(如从小到大排序),下一次循环是将其他的数进行类似操作。
* 性能:比较次数O(n^2),n^2/2;交换次数O(n^2),n^2/4
*
* @param data
* 要排序的数组
* @param sortType
* 排序类型
* @return
*/
public void bubbleSort(int[] data, String sortType) {
if (sortType.equals("asc")) { // 正排序,从小排到大
// 比较的轮数
for (int i = 1; i < data.length; i++) {
// 将相邻两个数进行比较,较大的数往后冒泡
for (int j = 0; j < data.length - i; j++) {
if (data[j] > data[j + 1]) {
// 交换相邻两个数
swap(data, j, j + 1);
}
}
}
} else if (sortType.equals("desc")) { // 倒排序,从大排到小
// 比较的轮数
for (int i = 1; i < data.length; i++) {
// 将相邻两个数进行比较,较大的数往后冒泡
for (int j = 0; j < data.length - i; j++) {
if (data[j] < data[j + 1]) {
// 交换相邻两个数
swap(data, j, j + 1);
}
}
}
} else {
System.out.println("您输入的排序类型错误!");
}
printArray(data);// 输出冒泡排序后的数组值
}
/**
* 直接选择排序法----选择排序的一种 方法:每一趟从待排序的数据元素中选出最小(或最大)的一个元素,
* 顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。 性能:比较次数O(n^2),n^2/2 交换次数O(n),n
* 交换次数比冒泡排序少多了,由于交换所需CPU时间比比较所需的CUP时间多,所以选择排序比冒泡排序快。
* 但是N比较大时,比较所需的CPU时间占主要地位,所以这时的性能和冒泡排序差不太多,但毫无疑问肯定要快些。
*
* @param data
* 要排序的数组
* @param sortType
* 排序类型
* @return
*/
public void selectSort(int[] data, String sortType) {
if (sortType.equals("asc")) { // 正排序,从小排到大
int index;
for (int i = 1; i < data.length; i++) {
index = 0;
for (int j = 1; j <= data.length - i; j++) {
if (data[j] > data[index]) {
index = j;
}
}
// 交换在位置data.length-i和index(最大值)两个数
swap(data, data.length - i, index);
}
} else if (sortType.equals("desc")) { // 倒排序,从大排到小
int index;
for (int i = 1; i < data.length; i++) {
index = 0;
for (int j = 1; j <= data.length - i; j++) {
if (data[j] < data[index]) {
index = j;
}
}
// 交换在位置data.length-i和index(最大值)两个数
swap(data, data.length - i, index);
}
} else {
System.out.println("您输入的排序类型错误!");
}
printArray(data);// 输出直接选择排序后的数组值
}
/**
* 插入排序 方法:将一个记录插入到已排好序的有序表(有可能是空表)中,从而得到一个新的记录数增1的有序表。 性能:比较次数O(n^2),n^2/4
* 复制次数O(n),n^2/4 比较次数是前两者的一般,而复制所需的CPU时间较交换少,所以性能上比冒泡排序提高一倍多,而比选择排序也要快。
*
* @param data
* 要排序的数组
* @param sortType
* 排序类型
*/
public void insertSort(int[] data, String sortType) {
if (sortType.equals("asc")) { // 正排序,从小排到大
// 比较的轮数
for (int i = 1; i < data.length; i++) {
// 保证前i+1个数排好序
for (int j = 0; j < i; j++) {
if (data[j] > data[i]) {
// 交换在位置j和i两个数
swap(data, i, j);
}
}
}
} else if (sortType.equals("desc")) { // 倒排序,从大排到小
// 比较的轮数
for (int i = 1; i < data.length; i++) {
// 保证前i+1个数排好序
for (int j = 0; j < i; j++) {
if (data[j] < data[i]) {
// 交换在位置j和i两个数
swap(data, i, j);
}
}
}
} else {
System.out.println("您输入的排序类型错误!");
}
printArray(data);// 输出插入排序后的数组值
}
/**
* 反转数组的方法
*
* @param data
* 源数组
*/
public void reverse(int[] data) {
int length = data.length;
int temp = 0;// 临时变量
for (int i = 0; i < length / 2; i++) {
temp = data[i];
data[i] = data[length - 1 - i];
data[length - 1 - i] = temp;
}
printArray(data);// 输出到转后数组的值
}
/**
* 快速排序 快速排序使用分治法(Divide and conquer)策略来把一个序列(list)分为两个子序列(sub-lists)。 步骤为:
* 1. 从数列中挑出一个元素,称为 "基准"(pivot), 2.
* 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分割之后,该基准是它的最后位置
* 。这个称为分割(partition)操作。 3. 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
* 递回的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递回下去,但是这个算法总会结束,因为在每次的迭代(iteration)
* 中,它至少会把一个元素摆到它最后的位置去。
*
* @param data
* 待排序的数组
* @param low
* @param high
* @see SortTest#qsort(int[], int, int)
* @see SortTest#qsort_desc(int[], int, int)
*/
public void quickSort(int[] data, String sortType) {
if (sortType.equals("asc")) { // 正排序,从小排到大
qsort_asc(data, 0, data.length - 1);
} else if (sortType.equals("desc")) { // 倒排序,从大排到小
qsort_desc(data, 0, data.length - 1);
} else {
System.out.println("您输入的排序类型错误!");
}
}
/**
* 快速排序的具体实现,排正序
*
* @param data
* @param low
* @param high
*/
private void qsort_asc(int data[], int low, int high) {
int i, j, x;
if (low < high) { // 这个条件用来结束递归
i = low;
j = high;
x = data[i];
while (i < j) {
while (i < j && data[j] > x) {
j--; // 从右向左找第一个小于x的数
}
if (i < j) {
data[i] = data[j];
i++;
}
while (i < j && data[i] < x) {
i++; // 从左向右找第一个大于x的数
}
if (i < j) {
data[j] = data[i];
j--;
}
}
data[i] = x;
qsort_asc(data, low, i - 1);
qsort_asc(data, i + 1, high);
}
}
/**
* 快速排序的具体实现,排倒序
*
* @param data
* @param low
* @param high
*/
private void qsort_desc(int data[], int low, int high) {
int i, j, x;
if (low < high) { // 这个条件用来结束递归
i = low;
j = high;
x = data[i];
while (i < j) {
while (i < j && data[j] < x) {
j--; // 从右向左找第一个小于x的数
}
if (i < j) {
data[i] = data[j];
i++;
}
while (i < j && data[i] > x) {
i++; // 从左向右找第一个大于x的数
}
if (i < j) {
data[j] = data[i];
j--;
}
}
data[i] = x;
qsort_desc(data, low, i - 1);
qsort_desc(data, i + 1, high);
}
}
/**
* 二分查找特定整数在整型数组中的位置(递归) 查找线性表必须是有序列表
*
* @paramdataset
* @paramdata
* @parambeginIndex
* @paramendIndex
* @returnindex
*/
public int binarySearch(int[] dataset, int data, int beginIndex, int endIndex) {
int midIndex = (beginIndex + endIndex) >>> 1; // 相当于mid = (low + high) 但是效率会高些
if (data < dataset[beginIndex] || data > dataset[endIndex] || beginIndex > endIndex){
System.out.println("找不到要查找的数字");
return -1;
}
if (data < dataset[midIndex]) {
return binarySearch(dataset, data, beginIndex, midIndex - 1);
} else if (data > dataset[midIndex]) {
return binarySearch(dataset, data, midIndex + 1, endIndex);
} else {
return midIndex;
}
}
/**
* 二分查找特定整数在整型数组中的位置(非递归) 查找线性表必须是有序列表
*
* @paramdataset
* @paramdata
* @returnindex
*/
public int binarySearch(int[] dataset, int data) {
int beginIndex = 0;
int endIndex = dataset.length - 1;
int midIndex = -1;
if (data < dataset[beginIndex] || data > dataset[endIndex] || beginIndex > endIndex)
return -1;
while (beginIndex <= endIndex) {
midIndex = (beginIndex + endIndex) >>> 1; // 相当于midIndex =
// (beginIndex +
// endIndex) / 2,但是效率会高些
if (data < dataset[midIndex]) {
endIndex = midIndex - 1;
} else if (data > dataset[midIndex]) {
beginIndex = midIndex + 1;
} else {
return midIndex;
}
}
return -1;
}
public static void main(String[] args) {
SortTest sortTest = new SortTest();
int[] array = sortTest.createArray();
System.out.println("==========冒泡排序后(正序)==========");
sortTest.bubbleSort(array, "asc");
System.out.println("==========冒泡排序后(倒序)==========");
sortTest.bubbleSort(array, "desc");
System.out.println();
array = sortTest.createArray();
System.out.println("==========倒转数组后==========");
sortTest.reverse(array);
System.out.println();
array = sortTest.createArray();
System.out.println("==========选择排序后(正序)==========");
sortTest.selectSort(array, "asc");
System.out.println("==========选择排序后(倒序)==========");
sortTest.selectSort(array, "desc");
System.out.println();
array = sortTest.createArray();
System.out.println("==========插入排序后(正序)==========");
sortTest.insertSort(array, "asc");
System.out.println("==========插入排序后(倒序)==========");
sortTest.insertSort(array, "desc");
System.out.println();
array = sortTest.createArray();
System.out.println("==========快速排序后(正序)==========");
sortTest.quickSort(array, "asc");
sortTest.printArray(array);
System.out.println("==========快速排序后(倒序)==========");
sortTest.quickSort(array, "desc");
System.out.println();
sortTest.printArray(array);
System.out.println("==========数组二分查找==========");
System.out.println("您要找的数在第" + sortTest.binarySearch(array,0) + "个位子。(下标从0计算)");
}
}
总结:
一、稳定性:
稳定:冒泡排序、插入排序、归并排序和基数排序
不稳定:选择排序、快速排序、希尔排序、堆排序
二、平均时间复杂度
O(n^2):直接插入排序,简单选择排序,冒泡排序。
在数据规模较小时(9W内),直接插入排序,简单选择排序差不多。当数据较大时,冒泡排序算法的时间代价最高。性能为O(n^2)的算法基本上是相邻元素进行比较,基本上都是稳定的。
O(nlogn):快速排序,归并排序,希尔排序,堆排序。
其中,快排是最好的, 其次是归并和希尔,堆排序在数据量很大时效果明显。
三、排序算法的选择
1.数据规模较小
(1)待排序列基本序的情况下,可以选择直接插入排序;
(2)对稳定性不作要求宜用简单选择排序,对稳定性有要求宜用插入或冒泡
2.数据规模不是很大
(1)完全可以用内存空间,序列杂乱无序,对稳定性没有要求,快速排序,此时要付出log(N)的额外空间。
(2)序列本身可能有序,对稳定性有要求,空间允许下,宜用归并排序
3.数据规模很大
(1)对稳定性有求,则可考虑归并排序。
(2)对稳定性没要求,宜用堆排序
4.序列初始基本有序(正序),宜用直接插入,冒泡
