Problem Description
2007年到来了。经过2006年一年的修炼,数学神童zouyu终于把0到100000000的Fibonacci数列
(f[0]=0,f[1]=1;f[i] = f[i-1]+f[i-2](i>=2))的值全部给背了下来。
接下来,CodeStar决定要考考他,于是每问他一个数字,他就要把答案说出来,不过有的数字太长了。所以规定超过4位的只要说出前4位就可以了,可是CodeStar自己又记不住。于是他决定编写一个程序来测验zouyu说的是否正确。
(f[0]=0,f[1]=1;f[i] = f[i-1]+f[i-2](i>=2))的值全部给背了下来。
接下来,CodeStar决定要考考他,于是每问他一个数字,他就要把答案说出来,不过有的数字太长了。所以规定超过4位的只要说出前4位就可以了,可是CodeStar自己又记不住。于是他决定编写一个程序来测验zouyu说的是否正确。
这题要用到对数和斐波那契数列公式
Input
输入若干数字n(0 <= n <= 100000000),每个数字一行。读到文件尾。
我们可以利用取对数把一个数变成我们想要的形式,例如1234567可以转化为1.234567具体过程如下:
log10(1234567)=log10(1.234567*10^6)=6+log10(1.234567);(log10(1.234567)为其小数部分)
10^(log10(1.234567))=1.234567;要去前四位只需乘以1000即可;
小于10000的那部分直接打出来。
另外就是数列公式的应用了公式如下:

取对数后
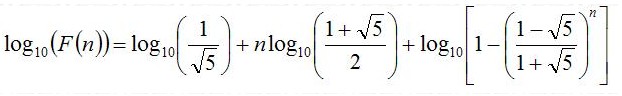
最后一项很小,可以忽略。
故log10(F(n))=-0.5*log10(5.0)+n*log10((1+sqrt(5))/2);
然后取其小数部分ans,pow(10.0,ans)(即10^ans),再乘以1000即可。代码如下:
#include<stdio.h>
#include<math.h>
int main()
{
int f[21]={0,1};
int n,i;
double ans;
for(i=2;i<21;i++)
f[i]=f[i-1]+f[i-2];
while(scanf("%d",&n)!=EOF)
{
if(n<21)
printf("%d
",f[n]);
else {
ans=-0.5*log10(5)+n*1.0*log10((1+sqrt(5))/2);
ans-=int(ans);
ans=pow(10.0,ans);
while(ans<1000)
ans*=10;
printf("%d
",int(ans));//这里不能用%.lf打印,%.lf会四舍五入的
}
}
return 0;
}