1、交通图的存储结构
定义交通图的存储结构。邻接矩阵是表示图形中顶点之间相邻关系的矩阵。设G=(V,E)是具有n个顶点的图,则G的邻接矩阵是具有如下定义的n阶方阵。
注:一个图的邻接矩阵表示是唯一的!其表示需要用一个二维数组存储顶点之间相邻关系的邻接矩阵并且还需要用一个具有n个元素的一维数组来存储顶点信息(下标为i的元素存储顶点的信息)。
邻接矩阵的存储结构:
#define MVNum 100 //最大顶点数
typedef struct
{
VertexType vexs[MVNum];//顶点数组,类型假定为char型
Adjmatrix arcs[MVNum][MVNum];//邻接矩阵,假定为int型
}MGraph;
注:由于有向图的邻接矩阵是不对称的,故程序运行时只需要输入所有有向边及其权值即可。
2、单源最短路径
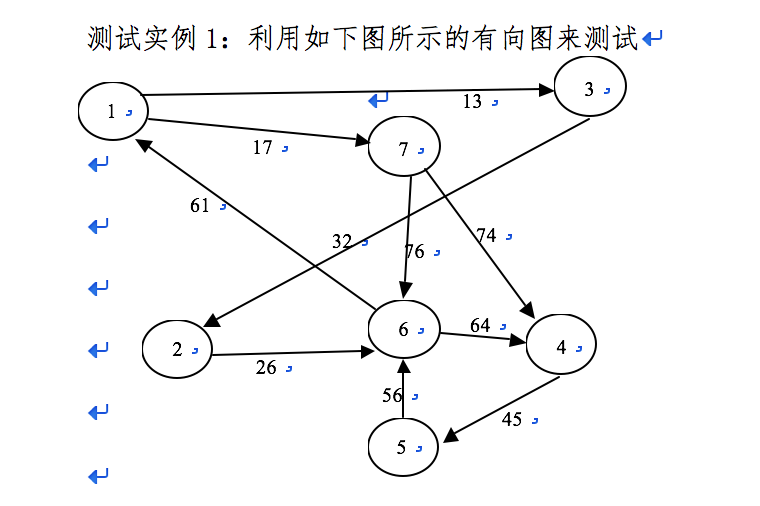
单源最短路径问题:已知有向图(带权),期望找出从某个源点S∈V到G中其余各顶点的最短路径。
迪杰斯特拉算法即按路径长度递增产生诸顶点的最短路径算法。
算法思想:设有向图G=(V,E),其中V={1,2,……n},cost是表示G的邻接矩阵,
cost[i][j]表示有向边<i,j>的权。若不存在有向边<i,j>,则cost[i][j] 的权为无穷大(这里取值为32767)。设S是一个集合,集合中一个元素表示一个顶点,从源点到这些顶点的最短距离已经求出。设顶点V1为源点,集合S的初态只包含顶点V1。数组dist记录从源点到其它各顶点当前的最短距离,其初值为dist[i]= cost[i][j],i=2,……n。从S之外的顶点集合V-S中选出一个顶点w,使dist[w] 的值最小。于是从源点到达w只通过S中的顶点,把w加入集合S中,调整dist中记录的从源点到V-S中每个顶点v的距离:从原来的dist[v]和dist[w]+cost[w][v]中选择较小的值作为新的dist[v]。重复上述过程,直到S中包含V中其余顶点的最短路径。
最终结果是:S记录了从源点到该顶点存在最短路径的顶点集合,数组dist记录了从源点到V中其余各顶点之间的最短路径,path是最短路径的路径数组,其中path[i]表示从源点到顶点i之间的最短路径的前驱顶点。
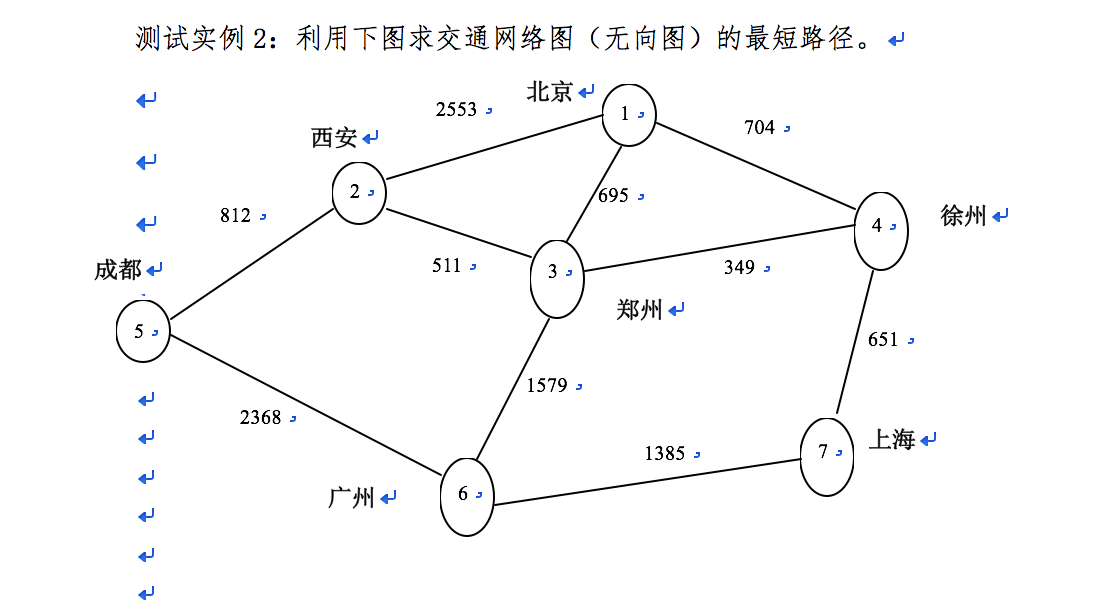
3、任意一对顶点之间的最短路径
任意顶点对之间的最短路径问题,是对于给定的有向网络图G=(V,E),要对G中任意一对顶点有序对,“V,W(V≠W)”,找出V到W的最短路径。而要解决这个问题,可以依次把有向网络图中每个顶点作为源点,重复执行前面的迪杰斯特拉算法n次,即可求得每对之间的最短路径。
费洛伊德算法的基本思想:假设求从Vi到Vj的最短路径。如果存在一条长度为arcs[i][j]的路径,该路径不一定是最短路径,还需要进行n次试探。首先考虑路径<vi,v1>和<v1,vj>是否存在。如果存在,则比较路径<vi.vj>和<vi,v1,vj>的路径长度,取长度较短者为当前所求得。该路径是中间顶点序号不大于1的最短路径。其次,考虑从vi到vj是否包含有顶点v2为中间顶点的路径< vi,…,v2,…,vj>,若没有,则说明从vi到vj的当前最短路径就是前一步求出的;若有,那么<vi,…,v2,…,vj>可分解为<vi,…,v2>和<v2,…,vj>,而这两条路径是前一次找到的中间点序号不大于1的最短路径,将这两条路径长度相加就得到路径<vi,…,v2,…vj>的长度。将该长度与前一次中求得的从vi到vj的中间顶点序号不大于1的最短路径比较,取其长度较短者作为当前求得的从vi到vj的中间顶点序号不大于2的最短路径。依此类推……直至顶点vn加入当前从vi到vj的最短路径后,选出从vi到vj的中间顶点序号不大于n的最短路径为止。由于图G中顶点序号不大于n,所以vi到vj的中间顶点序号不大于n的最短路径,已考虑了所有顶点作为中间顶点的可能性,因此,它就是vi到vj的最短路径。
程序代码:
//
// main.cpp
// Dijkstra
//
// Created by duanqibo on 2019/7/7.
// Copyright © 2019年 duanqibo. All rights reserved.
// Dijkstra 迪杰斯特拉-最短路径问题
#include <iostream>
#include<stdio.h>
#include<stdlib.h>
#define MVNum 100
#define Maxint 32767
enum boolean{FALSE,TRUE};
typedef char VertexType;
typedef int Adjmatrix;
typedef struct{
VertexType vexs[MVNum];
Adjmatrix arcs[MVNum][MVNum];
}MGraph;
int D1[MVNum],p1[MVNum];
int D[MVNum][MVNum],p[MVNum][MVNum];
void CreateMGraph(MGraph * G,int n,int e)
{
int i,j,k,w;
for(i=1;i<=n;i++)
G->vexs[i]=(char)i;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
G->arcs[i][j]=Maxint;
printf("输入%d条边的i.j及w: ",e);
for(k=1;k<=e;k++){
scanf("%d,%d,%d",&i,&j,&w);
G->arcs[i][j]=w;
}
printf("有向图的存储结构建立完毕! ");
}
void Dijkstra(MGraph *G,int v1,int n)
{
int D2[MVNum],p2[MVNum];
int v,i,w,min;
enum boolean S[MVNum];
for(v=1;v<=n;v++){
S[v]=FALSE;
D2[v]=G->arcs[v1][v];
if(D2[v]<Maxint)
p2[v]=v1;
else
p2[v]=0;
}
D2[v1]=0; S[v1]=TRUE;
for(i=2;i<n;i++){
min=Maxint;
for(w=1;w<=n;w++)
if(!S[w] && D2[w]<min)
{v=w;min=D2[w];}
S[v]=TRUE;
for(w=1;w<=n;w++)
if(!S[w] && (D2[v]+G->arcs[v][w]<D2[w])){
D2[w]=D2[v]+G->arcs[v][w];
p2[w]=v;
}
}
printf("路径长度 路径 ");
for(i=1;i<=n;i++){
printf("%5d",D2[i]);
printf("%5d",i);v=p2[i];
while(v!=0){
printf("<-%d",v);
v=p2[v];
}
printf(" ");
}
}
void Floyd(MGraph *G,int n)
{
int i,j,k;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
if( G->arcs[i][j]!=Maxint)
p[i][j]=j;
else
p[i][j]=0;
D[i][j]=G->arcs[i][j];
}
for(k=1;k<=n;k++)
{
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
if(D[i][k]+D[k][j]<D[i][j]) {
D[i][j]=D[i][k]+D[k][j];
p[i][j]=p[i][k];
}
}
}
}
int main(int argc, const char * argv[])
{
MGraph *G;
int n,e,v,w,k;
int xz=1;
G=(MGraph *)malloc(sizeof(MGraph));
printf("输入图中顶点个数和边数n,e:");
scanf("%d,%d",&n,&e);
CreateMGraph(G,n,e);
while(xz!=0){
printf("************求城市之间最短路径************ ");
printf("========================================= ");
printf("1.求一个城市到所有城市的最短路径 ");
printf("2.求任意的两个城市之间的最短路径 ");
printf("========================================= ");
printf("请选择 :1或2,选择0退出: ");
scanf("%d",&xz);
if (xz==2){
Floyd(G,n);
printf("输入源点(或起点)和终点:v,w:");
scanf("%d,%d",&v,&w);
k=p[v][w];
if (k==0)
printf("顶点%d 到 %d 无路径! ",v,w);
else
{
printf("从顶点%d 到 %d 最短路径路径是:%d",v,w,v);
while (k!=w){
printf("--%d",k);
k=p[k][w];
}
printf("--%d",w);
printf("径路长度:%d ",D[v][w]);
}
}
else
if(xz==1)
printf("求单源路径,输入源点v :");
scanf("%d",&v);
Dijkstra(G,v,n);
}
printf("结束求最短路径,再见! ");
return 1;
}
运行结果:

