实训4.1

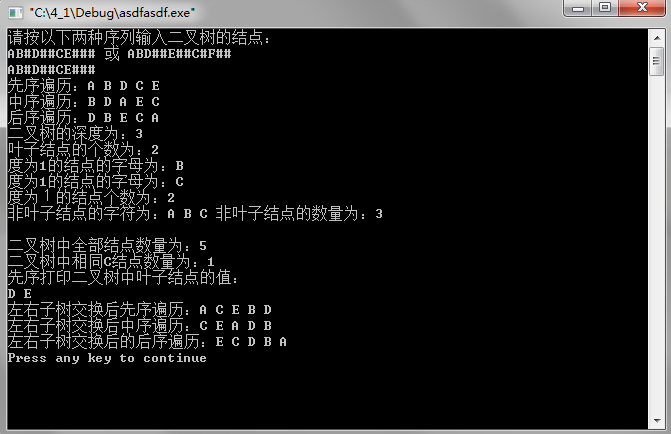
二叉树操作

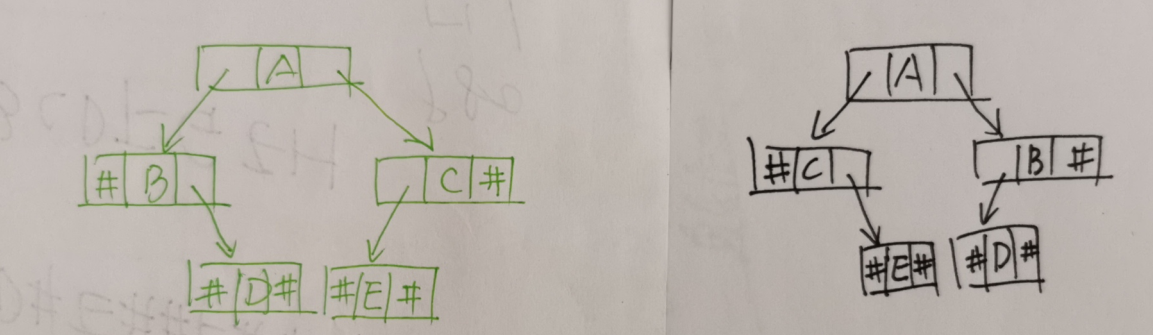左右子树交换后的二叉树

//二叉树的实现
#include <iostream>
using namespace std;
//二叉树的结点定义
typedef struct bitreenode
{
char data;
struct bitreenode *lchild,*rchild;
}*Bitree;
//创建二叉树
void creatbitree(Bitree &T)
{
char ch;
ch=getchar();
if(ch=='#')
T=NULL;
else
{
T=new bitreenode;
T->data=ch;
creatbitree(T->lchild);
creatbitree(T->rchild); //AB#D##CE###
}
}

//递归的方法先序遍历二叉树
void preordertraverse(Bitree T)
{
if(T!=NULL)
{
cout<<T->data<<" ";
preordertraverse(T->lchild);
preordertraverse(T->rchild);
}
}

//递归的方法中序遍历二叉树
void inordertraverse(Bitree T)
{
if(T)
{
inordertraverse(T->lchild);
cout<<T->data<<" ";
inordertraverse(T->rchild);
}
}

//递归的方法中序遍历二叉树
void postordertraverse(Bitree T)
{
if(T)
{
postordertraverse(T->lchild);
postordertraverse(T->rchild);
cout<<T->data<<" ";
}
}

//求二叉树的深度
int depthofbitree(Bitree T)
{
int ldepth,rdepth;
if(T==NULL)
return 0;
ldepth=depthofbitree(T->lchild);
rdepth=depthofbitree(T->rchild);
if(ldepth>rdepth)
return ldepth+1;
else
return rdepth+1;
}

//求叶子结点的个数
int leafcount(Bitree T)
{
if(T==NULL)
return 0;
else if(T->lchild==NULL && T->rchild==NULL)
return 1;
else
{
int n=leafcount(T->lchild);
int m=leafcount(T->rchild);
return m+n;
}
}

//输出二叉树中度为1的结点的值，并求其数量
int onesoncount(Bitree T)
{
if(T==NULL)
return 0;
else if((T->lchild!=NULL && T->rchild==NULL)||(T->rchild!=NULL && T->lchild==NULL))
{
cout<<"度为1的结点的字母为："<<T->data<<endl;
return onesoncount(T->lchild)+onesoncount(T->rchild)+1;
}
else
return onesoncount(T->lchild)+onesoncount(T->rchild);
}

//输出二叉树中所有度为2的结点的数据值，并统计其数目
int twoson(Bitree T)
{
if(T==NULL)
return 0;
else if(T->lchild!=NULL && T->rchild!=NULL)
cout<<"度为2的结点的字符是："<<T->data<<endl;
return twoson(T->lchild)+twoson(T->lchild) + 1;
}

//求二叉树T中非叶子结点的数目
int notleafcount(Bitree T)
{
if(T==NULL)
return 0;
else if(T->lchild==NULL && T->rchild==NULL)
return 0;
else
{
cout<<T->data<<" ";
int n=notleafcount(T->lchild);
int m=notleafcount(T->rchild);
return (m+n+1);
}
}

//求二叉树中全部结点的数量
int node_num(Bitree T)
{
if(T==NULL)
return 0;
else
return node_num(T->lchild)+node_num(T->rchild)+ 1;
}

//输出二叉树中的重复值
int same_node(Bitree T)
/*求二叉树结点数据域值为C的结点的数目*/
{
if(T== NULL )
return 0;
else
if (T->data=='C')
return(same_node(T->lchild)+same_node(T->rchild)+1);
else
return(same_node(T->lchild)+same_node(T->rchild));
}

//交换二叉树的左右子树
void Exchange(Bitree T)
{
Bitree temp=NULL;
if(T!=NULL)
{
temp=T->rchild;
T->rchild=T->lchild;
T->lchild=temp;
Exchange(T->lchild);
Exchange(T->rchild);
}
else
return;
}

//判断某个结点所在的层
int node_layer(Bitree T,int level,char key)
{
int l;
if(T)
{
if(T->data == key)
{
return level;
}
l = node_layer(T->lchild,level+1,key);
if(l != 0)
{
return l;
}
else
{
return node_layer(T->rchild,level+1,key) ;
}
}
return 0;
}

//按先序序列输出叶子结点的值
void preorder(Bitree T)
{
if(T)
{
if((T->lchild==NULL)&&(T->rchild==NULL))
cout<<T->data<<" ";
preorder(T->lchild);
preorder(T->rchild);
}
}

//主函数
int main()
{
Bitree t=NULL;
cout<<"请按以下两种序列输入二叉树的结点："<<endl;
printf("AB#D##CE### 或 ABD##E##C#F## ");
creatbitree(t);

cout<<"先序遍历：";
preordertraverse(t);
cout<<endl;

cout<<"中序遍历：";
inordertraverse(t);
cout<<endl;

cout<<"后序遍历：";
postordertraverse(t);
cout<<endl;

cout<<"二叉树的深度为："<<depthofbitree(t)<<endl;

int leaf=0;
leaf=leafcount(t);
cout<<"叶子结点的个数为："<<leaf<<endl;

int oneson1=0;
oneson1=onesoncount(t);
cout<<"度为１的结点个数为："<<oneson1<<endl;

int notleafcount1=0;
cout<<"非叶子结点的字符为：";
notleafcount1=notleafcount(t);
cout<<"非叶子结点的数量为："<<notleafcount1<<endl;
cout<<endl;

int all_node=0;
all_node=node_num(t);
cout<<"二叉树中全部结点数量为："<<all_node<<endl;

int same_num=0;
same_num=same_node(t);
cout<<"二叉树中相同C结点数量为："<<same_num<<endl;

//判断某个结点所在的层
int layer=1;
int la;
//char ch;


la=node_layer(t,layer,'C');
cout<<"结点C在的层是："<<la<<endl;

cout<<"先序打印二叉树中叶子结点的值："<<endl;
preorder(t);
cout<<endl;

Exchange(t);
cout<<"左右子树交换后先序遍历：";
preordertraverse(t);
cout<<endl;

cout<<"左右子树交换后中序遍历：";
inordertraverse(t);
cout<<endl;

cout<<"左右子树交换后的后序遍历：";
postordertraverse(t);
cout<<endl;

return 1;
}