一. 人员安排问题
- 问题定义:
-输入:
人员:P={ P1,P2…Pn} ; 工作:J={J1,J2…Jn} ; 矩阵[Cij]:表示Pi完成Jj的代价
限制条件:P是全序集,J是偏序集,要优先把高难度的任务分配给业务能力强的人员(即:分配任务的一 一映射函数f:若f(Pi) < f(Pj),则 Pi < Pj )
-输出:
[Xij]:Xij=1表示Pi完成Pj工作,否则Xij=0,使∑CijXij最小
- 算法设计
若无限制条件:最大二分匹配问题:匈牙利算法/最大流的FF算法
有限制条件:搜索的问题
- 如何转化成图的搜索问题
问题解空间:若 P1~>Jk1 , P2~>Jk2 ,…Pn~>Jkn , 则Jk1,Jk2,Jk3满足拓扑序
将可行解空间表示为拓扑树。
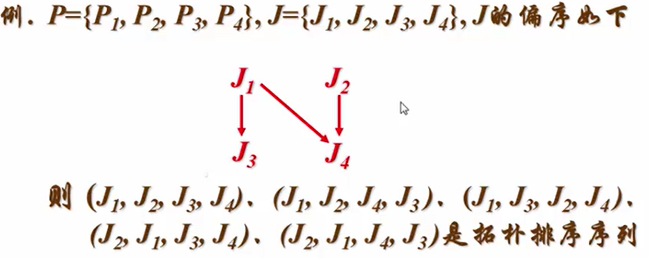
该问题的拓扑树如下
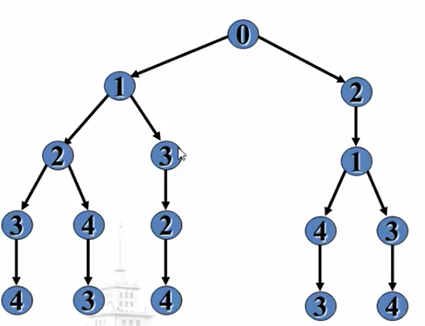
树高 i 表示Pi,结点 j 表示任务Jj
- 算法设计
(1)得到拓扑序列树
输入:偏序集合S,树根root
输出:由S的所有拓扑排序序列构成的树
1. 生成树根root
2. 选择偏序集合中没有前驱元素的所有元素,作为root的子节点
3. 对于root的每一个子节点v Do
4. S = S - {v}
5. 把v作为根,递归地处理S。
(2)分支界限求解
a. 得到每个步骤的尽可能大的下界:维护每个步骤尽可能大的下界的一个优先队列,有利于更快的剪枝
将矩阵[Cij]每行、列减去最小值,将减去的最小值求和得到初始问题的下界
b. 得到优化解的上界:用爬山法搜索得到一个可行解,作为优化解的上界
每次比较当前步骤的下界和优化解的上界来进行剪枝
c. 更新最优解的上界,重复步骤b,直到所有分支被剪去
二. 旅行商问题
- 问题定义:
输入:带权无环无向连通图G=(V,E)
输出:一条由任意节点开始,经过每个节点一次,最后返回开始节点的路径,该路径的代价最小。
- 算法设计
(1)可以使用上述问题中由每一步最大下界和整体上界的方法剪枝
上述方法每次只能剪去1/n的分支,在这里我们给出一种更优的思路:
改变解空间的定义方法,将问题的解空间表示成二叉树,这样可以一次剪去1/2的分支
(2)使用二叉树的分支界限法
a.预处理:[Xij] :表示i~>j的权值,二叉树T:结点表示路径,左子树表示包含该路径的解空间,右子树表示不包含该路径的解空间
b.剪枝技巧:1. [Xij]每行列减去最小值得到初始问题的下界
2. 结点表示路径的选取要使左右子树差距更大,利于剪枝
设最优选取的路径为ij,满足ij最小,且im + kj最大(矩阵点ij对应行列最小值的和最大)
c. 分支界限过程
左子树:贪心选择的局部最优解(获得问题的上界)
右子树:每一步骤对应的最大下界
d. 不断剪枝更新上界,直到分支为0,问题上界即为所求
注意:保证每次的上界是一个可行解(避免出现环)