//Copyright © 2018 dudujerry
//详细注释版线段树
#include<cstring> #include<iostream> #include<cmath> using namespace std; typedef long long ll; struct tre{ ll w,f; }; tre tree[400002]; ll reSum; int cl,cr; ll a[100002]; void ad(int k,ll v,int l,int r){ //这个函数是"缺失版区间修改",也就是改变当前节点的和,但是不用真的改变下层元素 //也就是添加懒标记,这个函数也可以下传懒标记,因为下传懒标记相当于在下层重新创建了一个懒标记 tree[k].w+=(r-l+1)*v; //在理论上这个节点代表的区间中每个元素应该加上v,所以树上这个节点应该加上:区间元素个数(r-l+1)乘上v tree[k].f+=v; //但是实际上我们不需要真的对涉及到的树上区间元素进行修改, //所以我们只需要为这一层添加懒标记,意思是这个节点代表的区间和的区间每一个元素都加上v } void pushdown(int k,int l,int r){ //lazy标记下传 if(tree[k].f==0) return; //如果没有标记就返回 int mid=(l+r)/2; ad(k*2,tree[k].f,l,mid); //将标记传给左儿子 ad(k*2+1,tree[k].f,mid+1,r); //让标记传给右儿子 tree[k].f=0; //已经下传完了,清除本层标记,那么就是我们之前提到过的下传懒标记 } void build(int k,int l,int r){ if(l==r){ tree[k].w=a[l]; //到叶节点,将线段元素放到树里 return; } int mid=(l+r)/2; //中间元素为(l+r)/2,此后不表 build(k*2,l,mid); //转移到左儿子 build(k*2+1,mid+1,r); //转移到右儿子 tree[k].w=tree[k*2].w+tree[k*2+1].w; //递归完之后更新当前元素 } void change_sec(ll v,int k,int l,int r){ if(r<cl||l>cr){ //如果离开了要改变的范围,就离开 return; //一定要return } if(l>=cl&&r<=cr){ //如果全部进入范围 ad(k,v,l,r); //知道了树上编号,也知道了目前要修改的区间,就可以用"缺失版区间修改" return; //一定要return } pushdown(k,l,r); //凡是涉及到元素修改/查询,在递归前都要下传懒标记 int mid=(l+r)/2; change_sec(v,k*2,l,mid); change_sec(v,k*2+1,mid+1,r); tree[k].w=tree[k*2].w+tree[k*2+1].w; //凡是涉及到元素修改的操作,在递归完成后都要更新当前节点的值 } void ask_sec(int k,int l,int r){ if(r<cl||l>cr) return; if(l>=cl&&r<=cr){ reSum+=tree[k].w; //查询到了l到r的和 return; } pushdown(k,l,r); int mid=(l+r)/2; ask_sec(k*2,l,mid); ask_sec(k*2+1,mid+1,r); //没有改变值,所以不用更新 } int main(){ ios_base::sync_with_stdio(0); //读入优化 cin.tie(0); //加了这个就不能用printf和scanf了 int n,m; cin>>n>>m; for(int i=1;i<=n;i++){ cin>>a[i]; } build(1,1,n); for(int i=0;i<m;i++){ int N=0; cin>>N; if(N==1){ ll k; int x,y; cin>>x>>y>>k; //k代表区间修改要加上的数 cl=x; //用全局变量记录要修改的范围 cr=y; //同上 change_sec(k,1,1,n); //意思是:在cl,cr区间加上k,从树上编号1和其对应的区间1,n开始递归 } else{ int x,y; cin>>x>>y; reSum=0; //用全局变量记录查询结果 cl=x; //范围,记录要查询的范围 cr=y; ask_sec(1,1,n); //意思是:从树上编号1和其对应的区间1,n开始递归 cout<<reSum<<endl; } } return 0; }
嗯...至于输入可以参考 https://www.luogu.org/problemnew/show/P3372
这篇代码过了
让我介绍一下线段树:
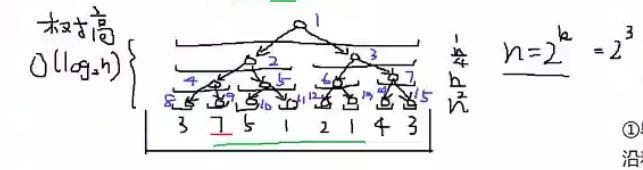
各位,这就是一棵线段树。
对于每个非叶节点,其左儿子右儿子分别维护它一半的区间。
例如,a负责[1~8]区间,则其左儿子l负责[1~4],右儿子
而我们需要给这些节点编号,设根编号为o,则左儿子编号为o*2,右儿子编号为o*2+1。
这样,单点修改的时候只需要O(logn)的时间就可以完成。
区间查询,类似分块的思想,对于非叶节点直接加上其维护的信息,剩余的叶节点则直接加上去。
区间修改,同样运用分块的思想,但是如果完全与区间查询的做法一样,时间复杂度反而高于朴素做法。于是我们这里引入一个“懒标记”的概念。
在修改到某完全属于目标区间的节点时(一个非叶节点),停止向下递归,同时加上它所维护区间长度*要修改的值,以及打上一个值为要修改的值懒标记。
懒标记意味着,在这一层维护的信息中已经经过单位为“懒标记”的修改,下次遇到这个元素的时候要下传。
然后,在访问到这个元素的时候进行“懒标记”的下传,相当于对它的儿子节点,或者说区间,进行修改,加上它所维护区间长度*要维护的值,以及打上一个值为要修改的值的懒标记。
(在其它操作访问带有懒标记的元素时,就调用下传懒标记的函数,将懒标记下传一层。)
比如区间查询,在路过某元素时发现懒标记,于是懒标记下传。然后区间修改向下递归的时候,继续下传,于是一直下传到叶节点。
所以,我们就可以得到复杂度很低的区间修改。(线段树真是一种神奇的结构)
0.几个优化技巧
x/2用x>>1代替
要查询/修改某个区间,不要把左右端点数值放在递归函数参数中,会压系统栈,比较慢。
1.开数组需要开元素数量的4倍
struct tre{
ll w,f;
};
tre tree[4*MAXN];
2.在ad(对单独编号的点进行lazy下传)中注意进行存储的值时需要(r-l+1)*v,v为下传的值
void ad(int k,ll v,int l,int r){
tree[k].w+=(r-l+1)*v;
tree[k].f+=v;
}
3.pushdown,lazy下传只需要ad其左右儿子
void pushdown(int k,int l,int r){
if(tree[k].f==0)
return;
int mid=(l+r)/2;
ad(k*2,tree[k].f,l,mid);
ad(k*2+1,tree[k].f,mid+1,r);
tree[k].f=0;
}
4.build,change等涉及到区间修改的操作最后都要更新目前编号(例如求和)
tree[k].w=tree[k*2].w+tree[k*2+1].w;
5.判断区间的时候可以一开始判断,r<cl||l>cr(c*为要操作的区间);判断成功操作之后要return;
if(r<cl||l>cr){
return;
}
if(l>=cl&&r<=cr){
ad(k,v,l,r);
return;
}
6.修改和查询的时候都要调用pushdown
pushdown(k,l,r);
7.别忘了build!
build(1,1,n);
---------------------------------------------------------------------------------------------------------------------------