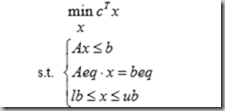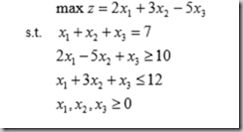线性规划问题是在一组线性约束条件下,求线性目标函数最大/最小值的问题。这些约束条件有不等式约束、等式约束以及边界约束,这和中学讲的线性规划无异。
此类问题的MATLAB标准形式为:
其中,max问题可以转换为min求解,三个约束条件分别为不等、等式、边界约束。
MATLAB求解函数:
[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
param:
c是目标系数;
A、b对应不等条件;
Aeq、beq对用等式条件;
LB、UB为边界;
x0是求解的初始值;
OPTIONS是控制参数,一般不用。
return:
x向量是使得目标函数最小的x取值;
fval是相应的目标函数最优值,若是由max问题转化为min,还要取反。
例题以及matlab求解:
一、求解线性规划问题
求解的matlab程序如下:
1 f = [-2;-3;5]; 2 A = [-2,5,-1;1,3,1]; 3 b = [-10;12]; 4 Aeq = [1,1,1]; 5 beq = 7; 6 lb = [0;0;0]; 7 ub = [inf;inf;inf]; 8 [x,y]=linprog(f,A,b,Aeq,beq,zeros(3,1)); 9 x 10 y = -y二、其他可以转换为线性规划问题,如目标为绝对值函数,指派问题(匈牙利算法),对偶理论与敏感度分析,在此略过,使用时查阅。
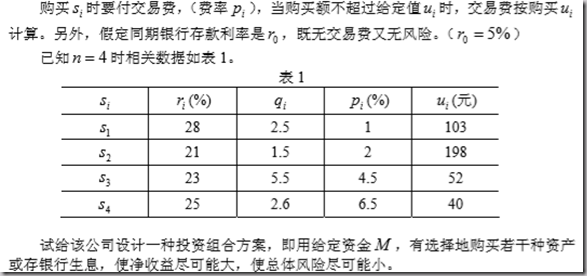
三、应用建模:投资的收益与风险
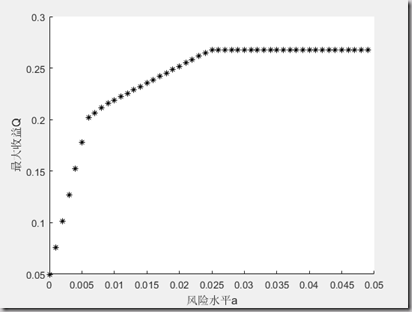
模型一的求解:
1 clc,clear 2 a = 0; 3 hold on 4 while a<0.05 5 c = [-0.05,-0.27,-0.19,-0.185,-0.185] 6 A = [zeros(4,1),diag([0.025,0.015,0.055,0.026])]; 7 b = a*ones(4,1); 8 Aeq = [1,1.01,1.02,1.045,1.065]; 9 beq = 1; 10 LB = zeros(5,1); 11 [X,Q] = linprog(c,A,b,Aeq,beq,LB); 12 Q = -Q; 13 Q 14 plot(a,Q,'*k'); 15 a = a + 0.001; 16 end 17 xlabel('风险水平a'); 18 ylabel('最大收益Q');结果分析: