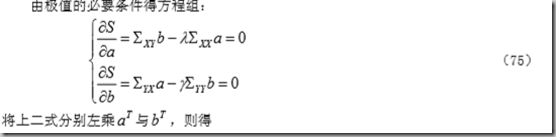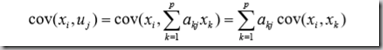【数学建模】day11-典型相关分析

这与主成分分析有点相似。

0. 基本思想
主成分分析（PCA）是把原始有相关性变量，线性组合出无关的变量（投影），以利用主成分变量进行更加有效的分析。
而典型相关分析（CCA）的思想是：

分析自变量组 X = [x1,x2,x3…xp]，因变量组 Y = [y1,y2,y3…yq] 之间的相关性。(注意这里X的每一个自变量x1是个列向量，代表有多个观测值)。

如果采用传统的相关分析，只要求X的每一个变量与Y的每一个变量的相关系数，从而组成相关系数矩阵 R = [r_ij]_p*q ,rij表示第i个自变量xi与第j个因变量yj之间的相关系数。

然而，这是有缺陷的：只粗暴的考虑了X与Y的关系，却忽略了X自变量之间也可能有相关关系，Y因变量之间亦如此。

解决的方法类似于主成分分析，我们可以把X提取出主成分，Y也提取出主成分，从而X、Y内部线性不相关了，这样利用主成分研究X与Y之间相关性就解决了上述缺点。

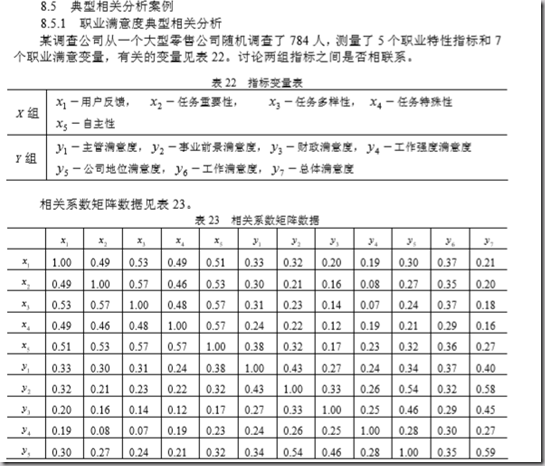
1. 典型相关分析

典型相关分析：

假设

自变量组：X = [x1,x2,x3…xp]

因变量组：Y = [y1,y2,y3…yq]

注意，xi与yj都是相同维度的列向量。

要求

分析X与Y之间的相关性

2 直观描述

首先在X中找出线性组合u1, 在Y中找出线性组合v1，使得 r(u1,v1)达到最大。

其次，在X中找第二个线性组合u2，Y中找第二个线性组合v2,要求使得u2与u1线性不相关，v2与v1线性不相关，并且: r(u2,v2)达到次大。

继续。直到两组变量之间的相关性被提取完毕。

3 数学描述

数学描述：

线性组合得到的变量称作典型变量。

4. 典型相关模型的分析

需要分析原始变量与典型变量之间的相关性。

原始变量xi与典型变量uj之间的相关性为：

式中，α是典型变量系数。

同理可求得原始变量xi与典型变量vj、yi与vj、yi与uj之间的相关系数。

建模时可以列出这四个相关系数表格。

进而，我们要对典型变量对各组原始变量解释能力做分析，因为原始变量-->典型变量毕竟会有信息的损失。

Def：

其中，ρ(ui,xk) 是指原始变量xk与电影变量ui之间的相关系数。

注：

1）这个解释能力是指，原始变量—>典型变量后，某个典型变量 ui 对原始变量<x1,x2,…xp>的解释能力。因为如果采用比较少的典型变量，就会有更多的信息损失，这与PCA分析中主成分贡献率类似。

2) 计算方法是：某个典型变量ui与所有xk(k=1 to p)的相关系数的平方和，再除以变量个数。这是方差比例。

我们还要进行典型相关系数的检验。

这一步是建模必须的。

计算典型相关系数用到的是，X与X之间的协方差矩阵、X与Y之间的协方差矩阵、Y与Y之间的协方差矩阵。而这些协方差矩阵其实是未知的，我们只是用一些样本对总体进行了近似。这个近似是有误差的，需要进行有关的假设检验。

即：整体检验：检验X与Y之间的协方差矩阵是否为0。若是0，则显然X与Y不相关。否则X与Y具有相关性，即说明至少第一对典型变量之间的相关性显著。

部分检验：检验部分典型相关系数为0的检验：也就是第k对典型相关变量之间相关关系不显著。

下面进行检验：

1）整体检验

2）部分总体典型相关系数为零的检验

5 Summary：典型相关分析步骤

步骤如下：

设标准化后，X、Y增广阵为Z：

step1：计算原始变量X、Y增广阵的相关系数矩阵R，并且剖分为：，其中，R11是X的协方差矩阵，R12是X与Y的协方差矩阵。

step2：求典型相关系数以及典型变量。

　　　　

step3：进行典型相关系数λi的显著性检验。有整体检验与部分检验，详情见上。

step4：典型结构与典型冗余分析。

这其实是计算：

典型结构分析：其实就是X组原始变量被ui解释分方差比例，Y组原始变量被vi解释的方差比例

典型冗余分析：其实就是X组原始变量被vi解释分方差比例，Y组原始变量被ui解释的方差比例

6. MATLAB实现。

MATLAB进行典型相关分析命令：

先查看一下Matlab help命令解释：

canoncorr Canonical correlation analysis.
    [A,B] = canoncorr(X,Y) computes the sample canonical coefficients for
    the N-by-P1 and N-by-P2 data matrices X and Y.  X and Y must have the
    same number of observations (rows) but can have different numbers of
    variables (cols).  A and B are P1-by-D and P2-by-D matrices, where D =
    min(rank(X),rank(Y)).  The jth columns of A and B contain the canonical
    coefficients, i.e. the linear combination of variables making up the
    jth canonical variable for X and Y, respectively.  Columns of A and B
    are scaled to make COV(U) and COV(V) (see below) the identity matrix.
    If X or Y are less than full rank, canoncorr gives a warning and
    returns zeros in the rows of A or B corresponding to dependent columns
    of X or Y.

   [A,B,R] = canoncorr(X,Y) returns the 1-by-D vector R containing the
    sample canonical correlations.  The jth element of R is the correlation
    between the jth columns of U and V (see below).

   [A,B,R,U,V] = canoncorr(X,Y) returns the canonical variables, also
    known as scores, in the N-by-D matrices U and V.  U and V are computed
    as

      U = (X - repmat(mean(X),N,1))*A and
       V = (Y - repmat(mean(Y),N,1))*B.

   [A,B,R,U,V,STATS] = canoncorr(X,Y) returns a structure containing
    information relating to the sequence of D null hypotheses H0_K, that
    the (K+1)st through Dth correlations are all zero, for K = 0:(D-1).
    STATS contains seven fields, each a 1-by-D vector with elements
    corresponding to values of K:

      Wilks:    Wilks' lambda (likelihood ratio) statistic
       chisq:    Bartlett's approximate chi-squared statistic for H0_K,
                 with Lawley's modification
       pChisq:   the right-tail significance level for CHISQ
       F:        Rao's approximate F statistic for H0_K
       pF:       the right-tail significance level for F
       df1:      the degrees of freedom for the chi-squared statistic,
                 also the numerator degrees of freedom for the F statistic
       df2:      the denominator degrees of freedom for the F statistic

   Example:

      load carbig;
       X = [Displacement Horsepower Weight Acceleration MPG];
       nans = sum(isnan(X),2) > 0;
       [A B r U V] = canoncorr(X(~nans,1:3), X(~nans,4:5));

      plot(U(:,1),V(:,1),'.');
       xlabel('0.0025*Disp + 0.020*HP - 0.000025*Wgt');
       ylabel('-0.17*Accel + -0.092*MPG')

   See also pca, manova1.

 

典型相关分析函数：[a,b,r,u,v,stats] = cononcorr(x,y):

param:

　　x：原始变量x矩阵，每列一个自变量指标，第i列是 xi 的样本值

　　y：原始变量y矩阵，每列一个因变量指标，第j列是 yj 的样本值

return:

　　a：自变量x的典型相关变量系数矩阵，每列是一组系数。

      　　列数为典型相关变量数

　　b：因变量y的典型相关变量系数矩阵，每列是一个系数

　　r： 典型相关系数。即第一对<u1,v1>之间的相关系数、第二对<u2,v2>之间的相关系数…

　　u：对于X的典型相关变量的值

　　v：对于Y的典型相关变量的值

　　stats：假设检验的值<详细用一下就知道了>

也可以使用MATLAB按照原理直接编写程序，一个实现的例子如下：

实现程序：

这个典型相关系数表中，第一列0.5537是第<u1,v1>的相关系数。