链接:https://ac.nowcoder.com/acm/contest/992/A
来源:牛客网
题目描述
目前,SARS 病毒的研究在世界范围内进行,经科学家研究发现,该病毒及其变种的 DNA 的一条单链中,胞嘧啶、腺嘧啶均是成对出现的。这虽然是一个重大发现,但还不是该病毒的最主要特征,因为这个特征实在太弱了。
为了进一步搞清楚该病毒的特征,CN 疾病控制中心和阿里巴巴集团合作,用科技的力量和程序的思维来解决这个难题。现阿里巴巴特委派你成为 CN 疾病控制中心的 SARS 高级研究员,去研究在这个特征下,可能成为 SARS 病毒的 DNA 序列的个数。更精确地说,你需要统计所有满足下列条件的长度为 n 的字符串的个数:
- 字符串仅由 A、T、C、G 组成
- A 出现偶数次(也可以不出现)
- C 出现偶数次(也可以不出现)
当 n=2 时,所有满足条件的字符串有如下 6个:
TT,TG,GT,GG,AA,CC。
注: 由于这个数可能非常庞大,你只需给出对 10^9+7 取模的结果即可。
输入描述:
多组输入(不超过10组),每行一个整数n:0 < n < 10^10^5
输出描述:
对于输入文件中的每一个 n,输出满足条件的字符串的个数对 10^9 +7 取模的结果。
示例1
输入
1 2 100
输出
2 6 113046907
析:首先这个一个生成函数的题目,从ACGT中可以知道,AC只能出现偶数次,而GT可以奇数,可以偶数,那么列出的生成函数是
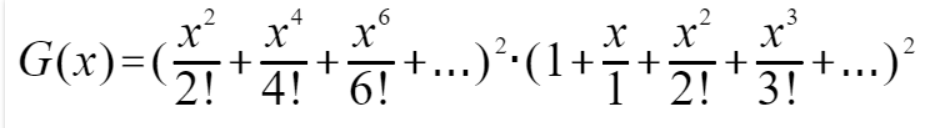 前面那个是AC的,后面那个是GT的,这样列出来之后,就只要算出
前面那个是AC的,后面那个是GT的,这样列出来之后,就只要算出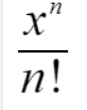 这一项的系数就是答案了。
这一项的系数就是答案了。
首先这个直接求是肯定求不出来的,要使用泰勒展式来求。


根据上面两个式子,可以对生成函数进行化简,化简后的结果就是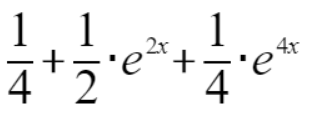
再根据泰勒展式, 求出
求出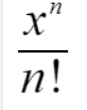 该项的系数。
该项的系数。
最终的结果就是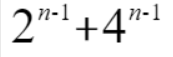 ,结果看起来很简单啊,但是 n 实在是太大了啊,所以还需要对 n 进行处理。
,结果看起来很简单啊,但是 n 实在是太大了啊,所以还需要对 n 进行处理。
假设求 2n 这个结果,首先是要对 1e9 + 7 进行取模的,根据欧拉定理 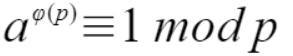 (其中 a 和 p 互质),根据本题来说那就是
(其中 a 和 p 互质),根据本题来说那就是 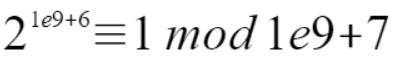
所以 2n %1e9+7就可以进行变形成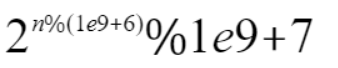 ,变成这样,那么指数就是肯定小于1e9 + 7 了,那么就可以使用快速幂来计算了。
,变成这样,那么指数就是肯定小于1e9 + 7 了,那么就可以使用快速幂来计算了。
代码如下:
#include <bits/stdc++.h>
using namespace std;
const long long mod = 1e9 + 7;
inline long long fast_pow(long long a, int n){
long long res = 1L;
while(n){
if(n&1) res = res * a % mod;
n >>= 1;
a = a * a % mod;
}
return res;
}
int main(){
string s;
while(cin >> s){
long long ans = 0;
for(int i = 0; i < s.size(); ++i)
ans = (ans * 10 + s[i] - '0') % (mod - 1);
ans = (ans - 2 + mod) % (mod - 1);
cout << (fast_pow(2, ans) + fast_pow(4, ans)) % mod << endl;
}
return 0;
}