一、题目
二、分析
公式很好推出来,就是$$a^{a^{a^{a^{...}}}}$$一共是$b$个$a$。
对于上式,由于指数太大,需要降幂,这里需要用到扩展欧拉定理:
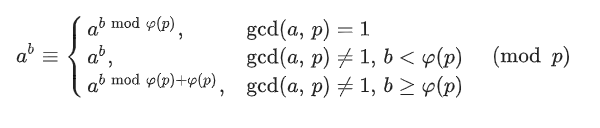
用这个定理时,除了$gcd (a,p) =1$的情况,其他情况主要是保证$a$的指数不为$0$,在写代码的时候也需要注意这点,当然也可以重新定义个快速幂,使其快速幂的结果保证不为$0$,也是可以的的。
三、AC代码
#include <bits/stdc++.h> using namespace std; #define ll long long #define Min(a,b) ((a)>(b)?(b):(a)) #define Max(a,b) ((a)>(b)?(a):(b)) #define P pair<int, int> const int MAXN = 1e6+5; int Phi[MAXN], Prime[MAXN], nPrime; void Euler() { memset(Phi, 0, sizeof(Phi)); Phi[1] = 1; nPrime = 0; for(int i = 2; i < MAXN; i++) { if(!Phi[i]) //i为素数 { Phi[i] = i - 1; Prime[nPrime++] = i; } for(int j = 0; j < nPrime && (long long)i*Prime[j] < MAXN; j++) { if(i%Prime[j]) { Phi[ i*Prime[j] ] = Phi[i]*(Prime[j]-1); } else { Phi[ i*Prime[j] ] = Phi[i]*Prime[j]; break; } } } return; } ll gcd(ll a, ll b) {return b==0?a:gcd(b,a%b);} ll Pow(ll a, ll b, ll mod) { ll ans = 1; while(b) { if(b&1) ans = ans*a%mod; a = a * a % mod; b>>=1; } return ans; } ll qPow(ll a, ll b, ll mod) { ll ans = 1; while(b) { if(b&1) ans = (ans * a > mod ? ans * a % mod + mod : ans * a); a = (a * a > mod ? a * a % mod + mod : a * a); b>>=1; } return ans; } ll solve(ll a, ll times, ll m) { if(m == 1) return 1; if(times == 0) return 1; ll res = Phi[m]; ll b = solve(a, times-1, res); if(gcd(a, m) == 1) return Pow(a, b%res, m); else if(b && b < res) return Pow(a, b, m); else return Pow(a, b%res + res, m); } ll solve2(ll a, ll times, ll m) { if(times == 0) return 1; if(m == 1) return 1; return qPow(a, solve2(a, times-1, Phi[m]), m); } int main() { freopen("input.txt", "r", stdin); //freopen("out.txt", "w", stdout); int T; ll a, b, m; scanf("%d", &T); Euler(); while(T--) { scanf("%lld%lld%lld", &a, &b, &m); printf("%lld ", solve2(a, b, m)%m); // printf("%lld ", solve(a, b, m)%m); } return 0; }