具体方法是加载此前算出的权重矩阵,每个内部点都是表面点的加权平均。
于是求解的时候唯一的未知数就是参数p了。
这次牛顿法能够模拟,但是同之前不带权重的模拟算法一样,模拟过程中无法收敛到全局极值点。
出问题的是这根棒。
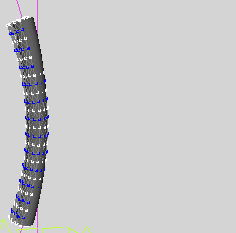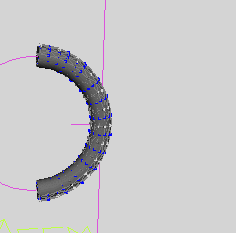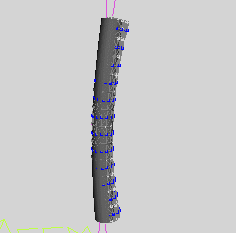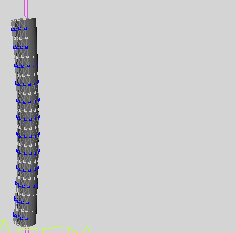
控制这根棒的参数有两个,一个是弯曲大小,另一个是弯曲方向。
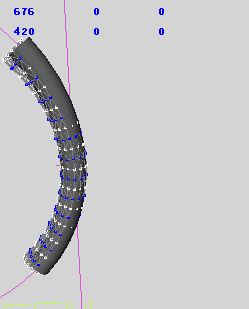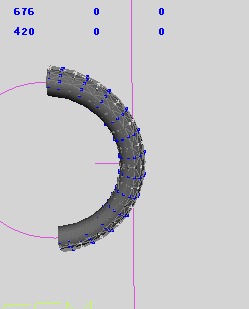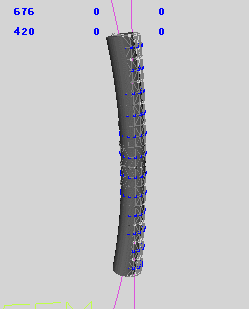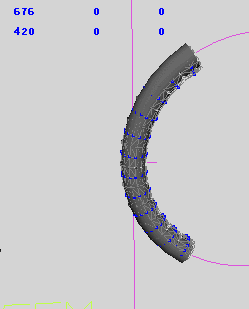
当强制令弯曲方向不起作用是,能够正常模拟,结果如上图。
当让弯曲方向参数起作用时,结果如下,模型不弯曲。

检查原因,发现牛顿法模拟的过程中,首步的梯度、Hessian、以及求出的参数增量如下:
| 梯度 | Hessian | 参数增量 | ||
| 有方向参数 | G=[21319.284966 ;0.000000 ;]; | H=[ 1734695.368102 7.202621 ; 7.202621 0.000000 ; ]; | x=1.0e+03 * [0 2.9599] | |
| 没有方向参数 | G=[21319.284966 ;0.000000 ;]; | H=[ 1734695.368102 0.000000 ; 0.000000 0.000000 ; ]; | x=[0.0123 0] |
准备在应用牛顿法前使用其他方法,例如沿梯度下降。
加了一个很简单的梯度下降算法
for (int ithIter = 0; ithIter < 5; ++ithIter){double f;isSucceed &= m_fem->computeValueAndGrad(p, tVec, &f, &G);p -= G * 1e-6;if(G.norm() < m_minGradSize)break;}
然后模拟成功了,如图……