HDU 1133 Buy the Ticket （数学、大数阶乘）

Buy the Ticket

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 8838    Accepted Submission(s): 3684

 

Problem Description

 

The "Harry Potter and the Goblet of Fire" will be on show in the next few days. As a crazy fan of Harry Potter, you will go to the cinema and have the first sight, won’t you?

Suppose the cinema only has one ticket-office and the price for per-ticket is 50 dollars. The queue for buying the tickets is consisted of m + n persons (m persons each only has the 50-dollar bill and n persons each only has the 100-dollar bill).

Now the problem for you is to calculate the number of different ways of the queue that the buying process won't be stopped from the first person till the last person.
Note: initially the ticket-office has no money.

The buying process will be stopped on the occasion that the ticket-office has no 50-dollar bill but the first person of the queue only has the 100-dollar bill.

 

 

Input

 

The input file contains several test cases. Each test case is made up of two integer numbers: m and n. It is terminated by m = n = 0. Otherwise, m, n <=100.

 

 

Output

 

For each test case, first print the test number (counting from 1) in one line, then output the number of different ways in another line.

 

 

Sample Input

3 0
3 1
3 3
0 0

Sample Output

Test #1:
6
Test #2:
18
Test #3:
180

题目大意

n+m个人排队买票，票价为50元，其中m个人各手持一张50元钞票，n个人各手持一张100元钞票，除此之外大家身上没有任何其他的钱币，并且初始时候售票窗口没有钱，问有多少种排队的情况数能够让大家都买到票。

题目分析

题解都说是要用到卡特兰数，但是仔细想了想卡特兰数没啥用呀.....算是他的一个变种，但是公式还是要现推的。

如果m=n，那么就是一个标准的卡特兰数，但是本题m和n不相等，不能直接用卡特兰的公式。

在不考虑不同的人的情况下，假设正确的方法有D_m+n个，无法满足题意的方法有W_n+m个，那么D_m+n +W_n+m =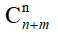

我们假设最早买不到票的人编号是k，他手持的是100元并且售票处没有钱，那么将前k个人的钱从50元变成100元，从100元变成50元，这时候就有m+1个人手持50元，n-1个手持100元的,也就是说W_n+m=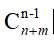

所以我们可以知道，D_m+n= -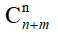

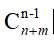
所以最终的答案化简为：（m+n)! * (m+1-n)/(m+1)

需要注意的是：

• 阶乘是个大数乘法
• 如何处理除法

 大数阶乘我之前的文章已经写过： 大数阶乘

 至于如何处理除法，我们可以我们注意到，如果n!=0，那么m+1必然会在前面的阶乘中求到，跳过不乘即可，最后再乘上个(m+1-n)就行了，如果n=0，那么只需要算前面的阶乘就好了，后面的因数是1。

代码

#include<bits/stdc++.h>

using namespace std;

int anss[1000000],m,n,cnt,temp,i,j,k,t=0;

int main()
{
    while(scanf("%d %d",&m,&n)&&(m!=0||n!=0))
    {
        t++;
        if(m<n)
        {
            cout<<"Test #"<<t<<':'<<endl;
            cout<<'0'<<endl;
            continue;
        }
        memset(anss,0,sizeof(anss)); 
        anss[1]=1;
        cnt=1;                            //记录当前结果长度 
        for(i=1;i<=n+m;i++)
        {
            if(i==m+1)
            continue;
            k=0;                        //记录进位 
            for(j=1;j<=cnt;j++)
            {
                temp=(anss[j]*i+k)%10;
                k=(anss[j]*i+k)/10;
                anss[j]=temp;
            } 
            while(k)
            {
                anss[++cnt]=k%10;
                k=k/10;
            }
        }
        if(n!=0)
        {
            k=0;                    
            for(j=1;j<=cnt;j++)
            {
                temp=(anss[j]*(m+1-n)+k)%10;
                k=(anss[j]*(m+1-n)+k)/10;
                anss[j]=temp;
            } 
            while(k)
            {
                anss[++cnt]=k%10;
                k=k/10;
            }
        }
        cout<<"Test #"<<t<<':'<<endl;
        for(i=cnt;i>=1;i--)
        printf("%d",anss[i]);
        cout<<endl;
    }
}