1.何为稀疏线性关系?
稀疏线性关系的意思就是绝大多数的特征和样本输出没有关系,线性拟合后这些特征维度的系数会全部为0,只有少量和输出相关的特征的回归系数不为0,这就是“稀疏线性关系”。
2.何为鲁棒性、归纳偏好和奥卡姆剃刀原理?
1)鲁棒性一般指模型的健壮性、稳定性、泛化性。
2)归纳偏好:机器学习算法在学习过程中对某种类型假设的偏好称为『归纳偏好』。任何一个有效的机器学习算法必有其归纳的偏好,否则它将被假设空间中看似在训练集上『等效』的假设所迷惑,而无法产生确定的学习结果。例如在分类问题中,如果随机抽选训练集上等效的假设(可以认为所有的正反例并没有区别),那么它的分类结果其实是不确定的,这要根据它所选取的样本来决定,这样的学习显然是没有意义的。
3)奥卡姆剃刀原理:当两个假说具有完全相同的解释力和预测力时,我们以那个较为简单的假说作为讨论依据。剃刀原则不是一个理论而是一个原理,它的目的是为了精简抽象实体。大部分情况下,应用奥卡姆剃刀原理是合适的;但是这不代表奥卡姆剃刀就是正确的。剃刀原则并不是一种定理,而是一种思维方式,做决策树分析的时候,采用9个属性的预测性能和5个属性的预测性能是相似的,那么我们就会选择5个属性来预测。
3.什么是无偏估计?
无偏估计是用样本统计量来估计总体参数时的一种无偏推断。估计量的数学期望等于被估计参数的真实值,则称此估计量为被估计参数的无偏估计,即具有无偏性,是一种用于评价估计量优良性的准则。无偏估计的意义是:在多次重复下,它们的平均数接近所估计的参数真值。
举例理解:
比如我要对某个学校一个年级的上千个学生估计他们的平均水平(真实值,上帝才知道的数字),那么我决定抽样来计算。
我抽出一个10个人的样本,可以计算出一个均值。那么如果我下次重新抽样,抽到的10个人可能就不一样了,那么这个从样本里面计算出来的均值可能就变了,对不对?
因为这个均值是随着我抽样变化的,而我抽出哪10个人来计算这个数字是随机的,那么这个均值也是随机的。但是这个均值也会服从一个规律(一个分布),那就是如果我抽很多次样本,计算出很多个这样的均值,这么多均值们的平均数应该接近上帝才知道的真实平均水平。
如果你能理解“样本均值”其实也是一个随机变量,那么就可以理解为这个随机变量的期望是真实值,所以无偏(这是无偏的定义);而它又是一个随机变量,只是估计而不精确地等于,所以是无偏估计量。
4.协方差和协方差矩阵
均值,标准差,方差这些都是对一维数据的度量,那么协方差是对多维数据的度量,它代表两个特征之间的关联程度。
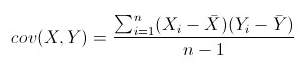
协方差的结果有什么意义呢?如果结果为正值,则说明两者是正相关的,结果为负值就说明负相关的,协方差多了就是协方差矩阵。
5.期望(数学期望,均值)
数学期望又称期望、均值,对于离散型数据,x属于X,每个x发生的概率是Px则期望为x1*Px1+...xn*Pxn
6.似然函数
在数理统计学中,似然函数是一种关于统计模型中的参数的函数,表示模型参数中的似然性。
7.概率和似然的区别
概率用于在已知一些参数的情况下,预测接下来的观测所得到的结果,而似然性则是用于在已知某些观测所得到的结果时,对有关事物的性质的参数进行估计。在这种意义上,似然函数可以理解为条件概率的逆反。
8.最大(极大)似然估计
总结起来,最大(极大)似然估计的目的就是:利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
原理:极大似然估计是建立在极大似然原理的基础上的一个统计方法,是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。
9.熵,交叉熵,相对熵(KL散度)

log是以2或者e为底的对数。
注意交叉熵和相对熵都是基于两概率分布进行衡量的,一般对目标类别标签进行独热编码,对求得的数据进行softmax转换,转换成符合概率分布的。
交叉熵常作为神经网络分类模型的损失函数,p代表正确答案,q代表预测值,通过交叉熵计算这两个概率分布之间的距离,交叉熵的值越小,两个概率分布越接近。
10、何为正态分布(又称高斯分布)?为什么会在机器学习中得到广泛的应用?
正态分布(Normal distribution),也称“常态分布”,又名高斯分布,是一个在数学、物理及工程等领域都非常重要的概率分布,正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布,记为N(μ,σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
那么为什么正态分布会在机器学习中得到广泛的应用?
机器学习基于统计学用的较多的是统计机器学习,统计学习的基础是统计,统计的基础之一就是中心极限定理,中心极限定理的结果就是高斯分布。
中心极限定理。说白了就是一大堆乱七八糟的(有界)随机变量加起来就像是高斯分布,这使得实际遇到的很多分布(如噪声等)近似服从高斯分布。
正态分布在现实中很多地方都能得到利用。