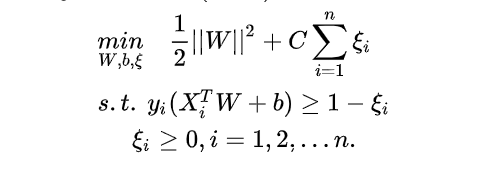我们说“训练”支持向量机模型,其实就是确定"最大间隔超平面"。
用数学语言来说就是确定一个最优的W。好比训练一个逻辑回归模型![]() 的目的是确定最优的W和b。
的目的是确定最优的W和b。
输入 X,为一个n维向量
输出 y,为-1或1
1.”弱鸡版支持向量机“——硬间隔 线性支持向量机(1962)
我更喜欢叫它 ”弱鸡版支持向量机“,因为它还什么都没有。
判别函数 f(X) = sign( W*X + b )。
我们要根据训练数据集{(X,y)}来计算出最优的参数W和b。
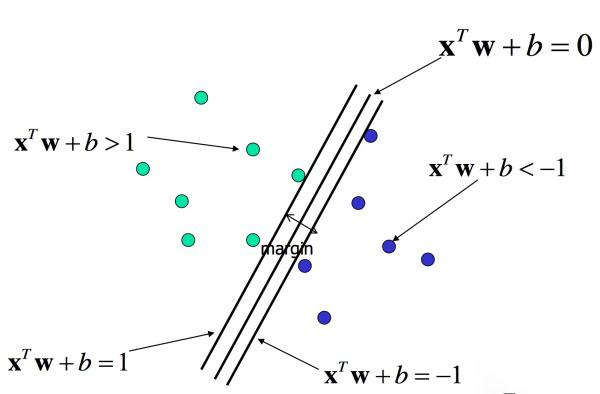
首先基于训练数据集我们有限制条件: y(i) * (W*X(i)+b) >=1,对于训练集中所有的(X(i) ,y(i))。
在此基础上我们找最优的W,也就是使margin = 2 / ||W|| 最大。
总结下来,即求解下面问题,解出最优的W和b。(相比之下,现代神经网络的求解是对于多项式目标函数J(W)求解使J(W)最小的W。只需要使用链式法则和求导计算这两个简单的数学技巧,这应该算是一个明显的进步吧)
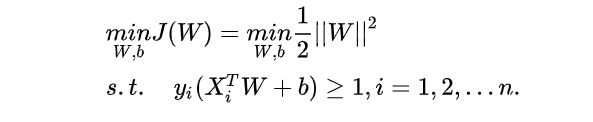
拉格朗日乘子法转换为对偶问题,再KKT条件,
具体数学解决过程这里不写了,较为繁琐。
我们在求解过程中引入了一组拉格朗日乘子,a1,a2,a3,a4.....
推导出:
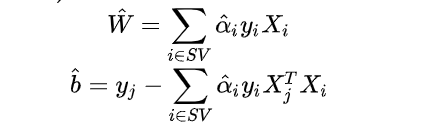
(SV是支持向量们的集合)
解出上式即可。
可以看出,最初支持向量机就是一个完全的数学模型。
2.“勃起版支持向量机”————软间隔 线性支持向量机(1962年)
在前面的硬间隔线性支持向量机上做了一些变化,即给目标函数加了铰链损失项,目标函数变为
J(W) = ![]()
其中称为惩罚参数,
越小时对误分类惩罚越小,越大时对误分类惩罚越大,当
取正无穷时就变成了硬间隔优化。实际应用时我们要合理选取
,
越小越容易欠拟合,
越大越容易过拟合。
(下面用ξ表示铰链函数)
接下来只要采用同样方法求解下面问题即可。