<强化学习>马尔可夫决策过程MDP

一.MDP  / NFA    ：马尔可夫模型和不确定型有限状态机的不同

状态自动机：https://www.cnblogs.com/AndyEvans/p/10240790.html

MDP和NFA唯一相似的地方就是它们都有状态转移，抛掉这一点两者就八竿子打不着了。

 

 

 

二.MP  -> MRP -> MDP

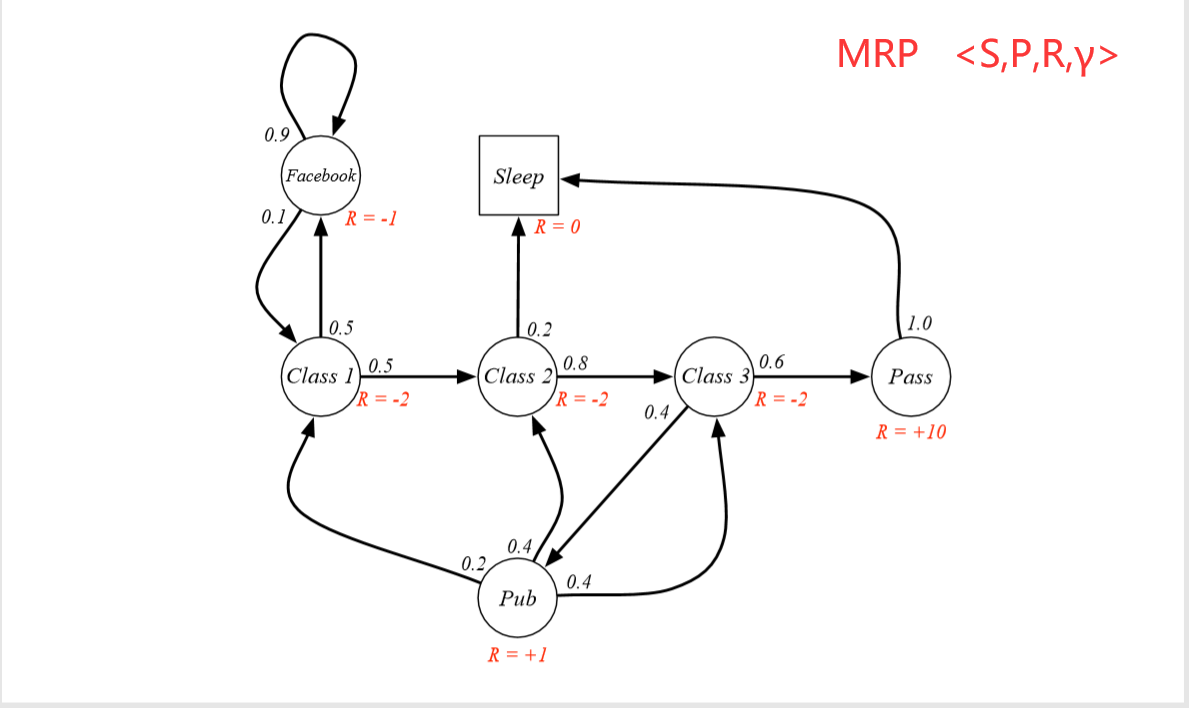
三.计算给定策略下的价值函数 / 贝尔曼期望方程

我们用贝尔曼期望方程求解在某个给定策略π和环境ENV下的价值函数：

具体解法是：（下面是对于V(s)的解法）

 

从而对于每一个特定的π，都能得到其对应的价值函数。所以我们可以有一组的{ (π₁,value_function_of_π₁) ，(π₂,value_function_of_π₂) ......  }

但是我们解决问题的目标是拿到最优的那组，其他的扔掉，解决方法就是使用贝尔曼最优方程确定最优价值函数。

 

 

四. 确定最优价值函数 /贝尔曼最优方程 

我们的“最优价值函数”和“最优策略”是如下定义的，找最优价值函数的过程也就是找最优策略的过程

 

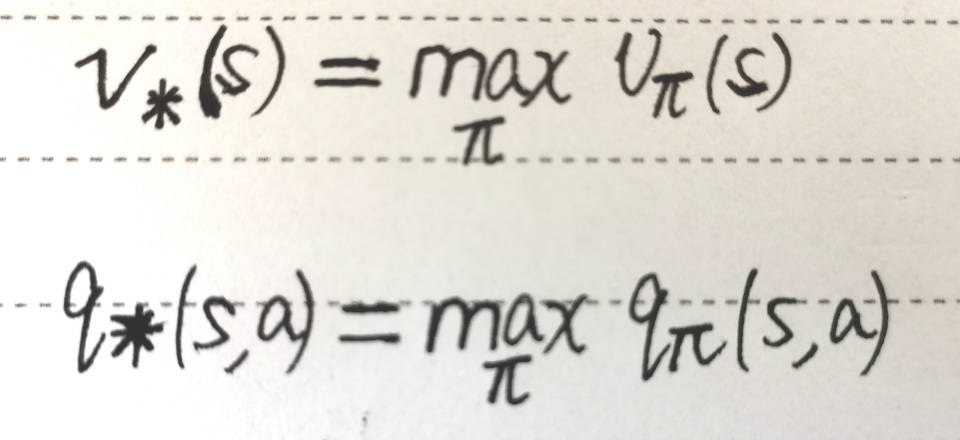
　　最优价值函数     ====    一个MDP中的可能的最好的表现

 

　　解决一个MDP    ====    确定唯一的最优价值函数

 

 

 

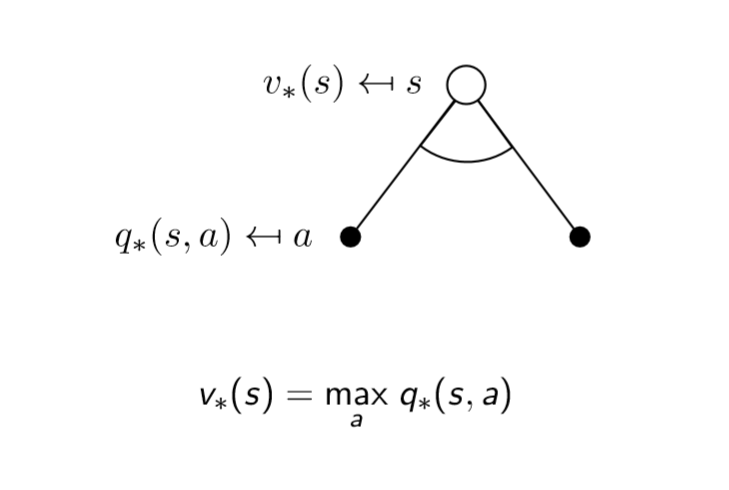
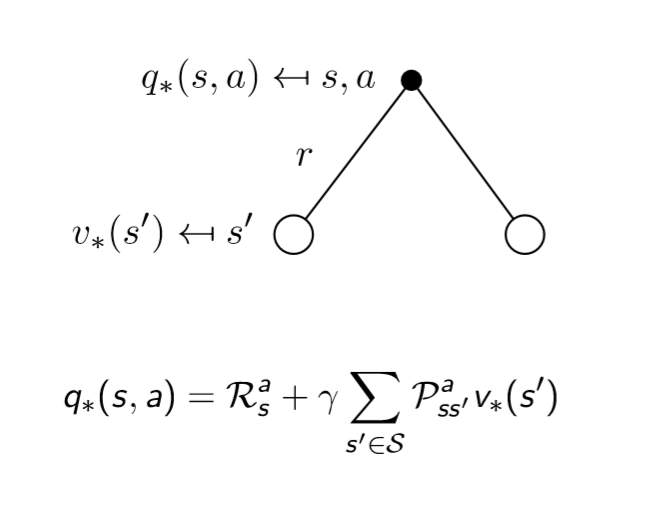
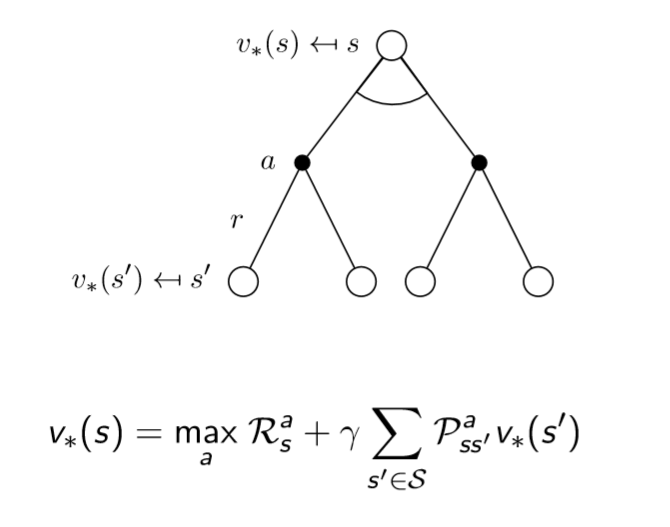
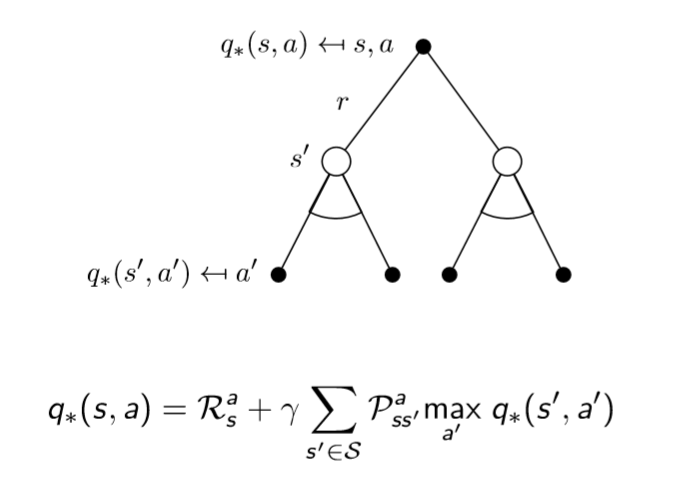
 传统的强化学习算法就是找定“最优价值”&“最优策略”的算法，好比SVM是要找定“最大间隔超平面”（“传统”和“现代”相区分，“现代”强化学习算法都是使用神经网络将其不确定化，转化为一个回归问题，训练模型参数，抛弃了“传统”方法的数学硬推）。

贝尔曼最优方程是非线性的，没有一个固定解法。所以，你就知道这是最原始的强化学习问题就好了，没有人会用这个硬推来解决强化学习问题的。

比它稍微高级一点儿，我们采用迭代法来求解最优价值最优策略：

——Value iteration

——Policy iteration

——Q-learning

——Sarsa

——Sarsa(lamda)

 

 

五.无限MDP和连续MDP

转换为离散MDP即可。

六.POMDP

 

 

 

七.Undiscounted average reward MDP