62. Unique Paths

Problem:

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

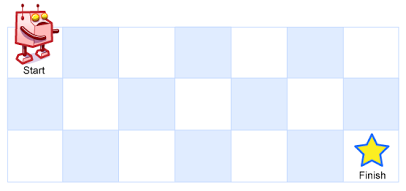
Above is a 7 x 3 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

Example 1:

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

Example 2:

Input: m = 7, n = 3
Output: 28

思路：
利用DP算法。设二维数组dp[i][j]表示从起点到达点(i,j)的方法总数，则只能从点(i-1,j)或(i,j-1)到达点(i,j)，故有dp[i][j]=dp[i-1][j]+dp[i][j-1]，最后返回dp[m-1][n-1]即可。注意赋初值时，dp[i][0]=dp[0][j]=1，因为在边界上只有一种方法可以到达。
实际上用数学方法很好解释。从起点到中间总共要向右走n-1步，向下走m-1步，总共需要走m+n-2步，只需要计算出m+n-2步中m-1步的组合数即可，即(C_{m+n-2}^{m-1})。

Solution:

int uniquePaths(int m, int n) {
    vector<vector<int>> dp(m, vector<int>(n, 1));
    
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++)
            dp[i][j] = dp[i-1][j] + dp[i][j-1];
    }
    
    return dp[m-1][n-1];
}

性能：
Runtime: 8 ms  Memory Usage: 8.7 MB