CF1089I Interval-Free Permutations

CF1089I Interval-Free Permutations

题目大意

题目链接

蔡老板是至高无上的世界首富，他手下有 (n) 名小弟（二五仔），编号为 (1dots n)。这些二五仔站成一排。从左到右，他们的编号构成了一个排列 (p_1, p_2, dots p_n)。

对于排列的一个子段 (p_l, p_{l+1}, dots, p_{r-1}, p_{r})，如果 (1 < r - l + 1 < n)，且将这个子段排序后是连续的一段数值，则这个子段里的二五仔们会叛变。

蔡老板要培养忠肝义胆的二五仔，因此不希望手下叛变。请你帮蔡老板数一数：有多少个长度为 (n) 的排列，满足没有子段会叛变呢？答案对一个质数 (P) 取模。

本题一个测试点里有 (T) 组测试数据，但他们的模数 (P) 相同。

数据范围：(1leq Tleq 400)，(10^8 leq Pleq 10^9)，(1leq nleq 400)。

本题题解

考虑用总数（(n!)）减去不合法的排列数。我们现在要研究不合法的排列长什么样。

称【将子段排序后是连续的一段数值】是子段（也就是原题题面中的 interval）为不合法子段。那么合法的排列，就是不存在长度在 ([2, n - 1]) 中的不合法子段的排列。

称一个不合法子段是极长的，当且仅当不存在另一个长度小于 (n) 的不合法子段包含它。发现，两个不合法子段如果有交，则它们的并也是不合法子段。因此，不合法的排列只有如下两种可能：

• 由两段极长不合法子段组成，这两段不合法子段可能相交。形式化地，若这两个子段分别是 ([l_1, r_1], [l_2, r_2])，则 (l_1 = 1, r_2 = n)，且 (r_1geq l_2 - 1)。
• 由三段及以上的极长不合法子段拼成，它们互不相交。形式化地，若这些子段分别是 ([l_1, r_2], [l_2, r_2], dots [l_k, r_k])，则 (l_1 = 1, r_k = n)，且 (forall 1leq i < k: r_i + 1 = l_{i + 1})。

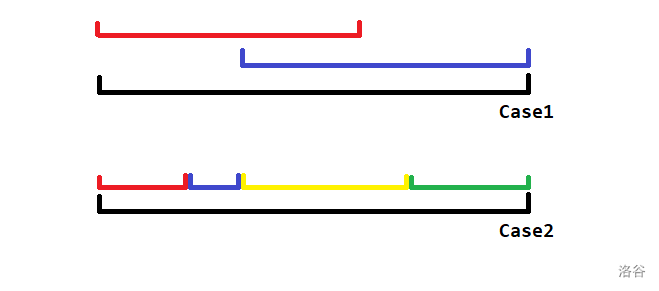
上述两种情况，不重不漏地刻画了所有不合法排列。因此只需要对这两种情况分别计数。

设长度为 (i) 的合法排列数为 (f(i))，也就是答案。

第一种不合法排列：发现两个子段中，必有一个包含的数值为 (1, 2, dots, i)（其中 (i) 是子段长度）。不妨假设它是左边的子段，然后把方案数乘以 (2) 即可。设 (h(i)) 表示有多少长度为 (i) 的排列，满足它的任何长度 (< i) 的前缀，不是【数值的一个前缀】。形式化地 (forall 1leq j < i: {p_k | k leq j} eq {1dots j})。求 (h(i))，可以继续使用【总数减不合法数量】的思想：(h(i) = i! - sum_{j = 1}^{i - 1}h(j)cdot (i - j)!)。求出 (h(i)) 后，第一种不合法的排列数量是 (2cdot sum_{i = 1}^{n - 1} h(i)cdot (n - i)!)。也就是枚举了左边子段的长度，后面的数可以任意排列：因为不管左边怎么样，后面任意排列，至少自己内部是一个不合法子段（(i + 1dots n)，连续的数值）；当然，它可能还能向左延伸一点，也就是两个子段有交。

第二种不合法排列：考虑设 (g(i, j)) 表示 (i) 个数，划分为 (j) 个不合法子段的方案数（不一定极长）。则：(g(i, j) = sum_{k = 1}^{i}g(i - k, j - 1)cdot k!)，其中枚举的 (k) 是最后一个不合法子段的长度（这个子段内部可以任意排列，也就是 (k!) 种方案）。边界是 (g(0, 0) = 1)。注意，这里没有考虑子段的相对顺序，也就是最后一个子段里的数值，默认为 (i - k + 1dots i)。给此时的 (j) 个子段依次编号为 (1dots j)。现在要求 (j) 个子段都是极长的，那么相当于 (1dots j) 这些子段的子段，不能有连续数值，也就是：(sum_{j = 3}^{n - 1}g(n, j)cdot f(j))。

综上所述：

[f(n) = n! - 2cdot sum_{i = 1}^{n - 1} h(i)cdot (n - i)! - sum_{j = 3}^{n - 1}g(n, j)cdot f(j) ]

预处理答案，时间复杂度 (mathcal{O}(n^3))。

参考代码

// problem: CF1089I
#include <bits/stdc++.h>
using namespace std;

#define mk make_pair
#define fi first
#define se second
#define SZ(x) ((int)(x).size())

typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;

template<typename T> inline void ckmax(T& x, T y) { x = (y > x ? y : x); }
template<typename T> inline void ckmin(T& x, T y) { x = (y < x ? y : x); }

const int MAXN = 400;
int MOD;

inline int mod1(int x) { return x < MOD ? x : x - MOD; }
inline int mod2(int x) { return x < 0 ? x + MOD : x; }
inline void add(int &x, int y) { x = mod1(x + y); }
inline void sub(int &x, int y) { x = mod2(x - y); }

int fac[MAXN + 5];
int h[MAXN + 5];
int g[MAXN + 5][MAXN + 5];
int f[MAXN + 5];

void init(int n) {
	
	fac[0] = 1;
	for (int i = 1; i <= n; ++i) {
		fac[i] = (ll)fac[i - 1] * i % MOD;
	}
	
	h[1] = 1;
	for (int i = 2; i <= n; ++i) {
		h[i] = fac[i];
		for (int j = 1; j < i; ++j) {
			sub(h[i], (ll)h[j] * fac[i - j] % MOD);
		}
	}
	
	g[0][0] = 1;
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= i; ++j) {
			for (int k = 1; k <= i; ++k) {
				add(g[i][j], (ll)g[i - k][j - 1] * fac[k] % MOD);
			}
		}
	}
	
	f[1] = 1; f[2] = 2;
	for (int i = 3; i <= n; ++i) {
		f[i] = 0;
		for (int j = 1; j < i; ++j) {
			add(f[i], (ll)h[j] * fac[i - j] % MOD);
		}
		f[i] = mod1(f[i] * 2);
		
		for (int j = 3; j < i; ++j) {
			add(f[i], (ll)g[i][j] * f[j] % MOD);
		}
		f[i] = mod2(fac[i] - f[i]); // 总 - 不合法
	}
}

int main() {
	int T;
	cin >> T;
	
	cin >> MOD;
	init(MAXN);
	
	while (T--) {
		int n;
		cin >> n;
		cout << f[n] << endl;
	}
	return 0;
}