图基本算法 图的表示方法 邻接矩阵 邻接表

　　

　　要表示一个图G=(V,E)，有两种标准的表示方法，即邻接表和邻接矩阵。这两种表示法既可用于有向图，也可用于无向图。通常采用邻接表表示法，因为用这种方法表示稀疏图（图中边数远小于点个数）比较紧凑。但当遇到稠密图（|E|接近于|V|^2）或必须很快判别两个给定顶点手否存在连接边时，通常采用邻接矩阵表示法，例如求最短路径算法中，就采用邻接矩阵表示。

　　图G=<V，E>的邻接表表示是由一个包含|V|个列表的数组Adj所组成，其中每个列表对应于V中的一个顶点。对于每一个u∈V，邻接表Adj[u]包含所有满足条件（u，v）∈E的顶点v。亦即，Adj[u]包含图G中所有和顶点u相邻的顶点。每个邻接表中的顶点一般以任意顺序存储。

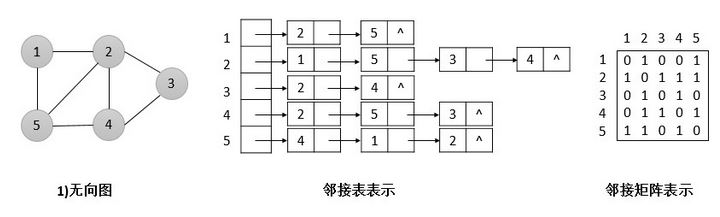
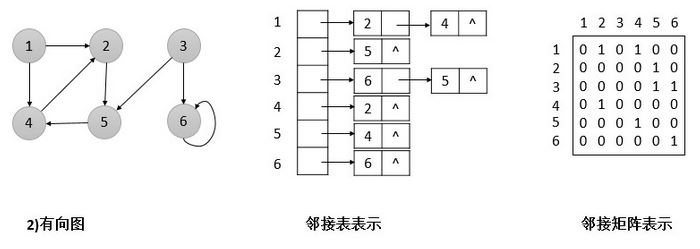
　　如果G是一个有向图，则所有邻接表的长度之和为|E|，这是因为一条形如（u，v）的边是通过让v出现在Adj[u]中来表示的。如果G是一个无向图，则所有邻接表的长度之和为2|E|，因为如果（u，v）是一条无向边，那么u会出现在v的邻接表中，反之亦然。邻接表需要的存储空间为O（V+E）。

　　邻接表稍作变动，即可用来表示加权图，即每条边都有着相应权值的图，权值通常由加权函数w：E→R给出。例如，设G=<V，E>是一个加权函数为w的加权图。对每一条边（u，v)∈E，权值w（u，v）和顶点v一起存储在u的邻接表中。

邻接表C++实现:

#include <iostream>
#include <cstdio>
using namespace std;

#define maxn 100  //最大顶点个数
int n, m;       //顶点数，边数

struct arcnode  //边结点
{
    int vertex;     //与表头结点相邻的顶点编号
    int weight = 0;     //连接两顶点的边的权值
    arcnode * next; //指向下一相邻接点
    arcnode() {}
    arcnode(int v,int w):vertex(v),weight(w),next(NULL) {}
    arcnode(int v):vertex(v),next(NULL) {}
};

struct vernode      //顶点结点，为每一条邻接表的表头结点
{
    int vex;    //当前定点编号
    arcnode * firarc;   //与该顶点相连的第一个顶点组成的边
}Ver[maxn];

void Init()  //建立图的邻接表需要先初始化，建立顶点结点
{
    for(int i = 1; i <= n; i++)
    {
        Ver[i].vex = i;
        Ver[i].firarc = NULL;
    }
}

void Insert(int a, int b, int w)  //尾插法，插入以a为起点，b为终点，权为w的边，效率不如头插，但是可以去重边
{
    arcnode * q = new arcnode(b, w);
    if(Ver[a].firarc == NULL)
        Ver[a].firarc = q;
    else
    {
        arcnode * p = Ver[a].firarc;
        if(p->vertex == b)  //如果不要去重边，去掉这一段
        {
            if(p->weight < w)
                p->weight = w;
            return ;
        }
        while(p->next != NULL)
        {
            if(p->next->vertex == b)    //如果不要去重边，去掉这一段
            {
                if(p->next->weight < w);
                    p->next->weight = w;
                return ;
            }
            p = p->next;
        }
        p->next = q;
    }
}
void Insert2(int a, int b, int w)   //头插法，效率更高，但不能去重边
{
    arcnode * q = new arcnode(b, w);
    if(Ver[a].firarc == NULL)
        Ver[a].firarc = q;
    else
    {
        arcnode * p = Ver[a].firarc;
        q->next = p;
        Ver[a].firarc = q;
    }
}

void Insert(int a, int b)   //尾插法，插入以a为起点，b为终点，无权的边，效率不如头插，但是可以去重边
{
    arcnode * q = new arcnode(b);
    if(Ver[a].firarc == NULL)
        Ver[a].firarc = q;
    else
    {
        arcnode * p = Ver[a].firarc;
        if(p->vertex == b) return;      //去重边，如果不要去重边，去掉这一句
        while(p->next != NULL)
        {
            if(p->next->vertex == b)    //去重边，如果不要去重边，去掉这一句
                return;
            p = p->next;
        }
        p->next = q;
    }
}
void Insert2(int a, int b)   //头插法，效率跟高，但不能去重边
{
    arcnode * q = new arcnode(b);
    if(Ver[a].firarc == NULL)
        Ver[a].firarc = q;
    else
    {
        arcnode * p = Ver[a].firarc;
        q->next = p;
        Ver[a].firarc = q;
    }
}
void Delete(int a, int b)   //删除以a为起点，b为终点的边
{
    arcnode * p = Ver[a].firarc;
    if(p->vertex == b)
    {
        Ver[a].firarc = p->next;
        delete p;
        return ;
    }
    while(p->next != NULL)
        if(p->next->vertex == b)
        {
            p->next = p->next->next;
            delete p->next;
            return ;
        }
}

void Show()     //打印图的邻接表（有权值）
{
    for(int i = 1; i <= n; i++)
    {
        cout << Ver[i].vex;
        arcnode * p = Ver[i].firarc;
        while(p != NULL)
        {
            cout << "->(" << p->vertex << "," << p->weight << ")";
            p = p->next;
        }
        cout << "->NULL" << endl;
    }
}

void Show2()     //打印图的邻接表(无权值）
{
    for(int i = 1; i <= n; i++)
    {
        cout << Ver[i].vex;
        arcnode * p = Ver[i].firarc;
        while(p != NULL)
        {
            cout << "->" << p->vertex;
            p = p->next;
        }
        cout << "->NULL" << endl;
    }
}
int main()
{
    int a, b, w;
    cout << "Enter n and m：";
    cin >> n >> m;
    Init();
    while(m--)
    {
        cin >> a >> b >> w;       //输入起点、终点
        Insert(a, b, w);        //插入操作
        Insert(b, a, w);        //如果是无向图还需要反向插入
    }
    Show();
    return 0;
}

 

　　

　　邻接表表示法也有潜在的不足之处，即如果要确定图中边（u,v）是否存在，只能在顶点u邻接表Adj[u]中搜索v，除此之外没有其他更快的办法。这一不足可通过图的邻接矩阵表示法来弥补，但要（在渐进意义下）以占用更多的存储空间为代价。

　　在图G=(V,E)的临界矩阵表示法中，假定各顶点按某种任意的方式编号为1,2,···，|V|，那么G的邻接矩阵为一个|V|*|V|的矩阵A=(a[i][j])，它满足：

　　观察无向图的邻接矩阵会发现，它是沿主对角线对称的。在一个无向图中，（u,v）和（v,u）表示同一条边，故无向图的邻接矩阵A的转置矩阵就是它本真。在某些应用中，可以只存储邻接矩阵的对角线以及对角线以上的部分，这样一来，图所占用的存储空间几乎可以减少一半。

　　邻接矩阵也可以用来表示加权图。例如，如果G=<V，E>是一个加权图，其权值函数为w，对于边（u，v）∈E，其权值w（u，v）就可以简单地存储在邻接矩阵的第u行第v列的元素中。如果边不存在，则可以在矩阵的相应元素中存一个NIL值，在很多问题中，对这样的元素赋0或∞会更为方便些。

邻接矩阵C++实现：

#include <iostream>
#include <cstdio>
using namespace std;

#define maxn 100
#define INF 1xffffff    //预定于的最大值
int n, m;   //顶点数、边数
int g[maxn][maxn];      //邻接矩阵表示

void Init()
{
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
        g[i][j] = 0;    //讲所有顶点度数置零，若为带权图，则置为INF
}
void Show() //打印邻接矩阵
{
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= n; j++)
            cout << g[i][j] << " ";
        cout << endl;
    }
}
int main()
{
    int a, b;
    cout << "Enter n and m:";
    cin >> n >> m;
    while(m--)
    {
        cin >> a >> b;  //输入为边的始点、终点，若有权，还需输入权w
        g[a][b] = 1;    //a、b间存在边，将g[a][b]置1，若有权，则将其置为权值
        g[b][a] = 1;    //对于无向图，还要插入边(b，a）
    }
    Show();
    return 0;
}

（文章以及相关代码参考算法导论编写）