一 Prim算法

/*POJ1258 有n个农场,已知这n个农场都互相相通,有一定的距离,现在每个农场需要装光纤, 问怎么安装光纤能将所有农场都连通起来,并且要使光纤距离最小,输出安装光纤的总距离 数据:(几个点,矩阵表示各点中间的距离) 4 0 4 9 21 4 0 8 17 9 8 0 16 21 17 16 0 */ #include <stdio.h> #include <string.h> #define MaxInt 0x3f3f3f3f #define N 110//创建map二维数组储存图表,low数组记录每2个点间最小权值,visited数组标记某点是否已访问 int map[N][N],low[N],visited[N]; int n; int prim() { int i,j,pos,min,result=0; memset(visited,0,sizeof(visited));//从某点开始,分别标记和记录该点 visited[1]=1;pos=1;//第一次给low数组赋值 for(i=1;i<=n;i++) if(i!=pos) low[i]=map[pos][i];//再运行n-1次 for(i=1;i<n;i++) {//找出最小权值并记录位置 min=MaxInt; for(j=1;j<=n;j++) if(visited[j]==0&&min>low[j]) { min=low[j];pos=j; }//最小权值累加 result+=min;//标记该点 visited[pos]=1;//更新权值 for(j=1;j<=n;j++) if(visited[j]==0&&low[j]>map[pos][j]) low[j]=map[pos][j]; } return result; } int main() { int i,v,j,ans; while(scanf("%d",&n)!=EOF) {//所有权值初始化为最大 memset(map,MaxInt,sizeof(map)); for(i=1;i<=n;i++) for(j=1;j<=n;j++) { scanf("%d",&v); map[i][j]=v; } ans=prim(); printf("%d ",ans); } return 0; }
图解prim


二 Kruskal算法

#include <iostream> #include <algorithm> using namespace std; const int NODE_NUM = 102; int father[NODE_NUM]; int n, ne; struct edge { int u,v,w; }; edge e[NODE_NUM*NODE_NUM]; bool cmp(const edge& a, const edge& b) { return a.w<b.w; } void make_set() { for (int i = 1; i <= n; ++i) father[i] = i; } int find_set(int i) { if (father[i] != i){ father[i] = find_set(father[i]); } return father[i]; } bool union_set(int a, int b) //a --> b { a = find_set(a); b = find_set(b); if (a != b){ //没有共同祖先,说明没有形成回路 father[a] = b; //将节点纳入最小生成树集合 return true; } else{ return false; } } int kruskal() { int i, mst_edge = 0, sum = 0; make_set(); sort(e, e+ne, cmp); //将边按升序排序 for (i = 0; i < ne; ++i)//如果加入的边不会使树形成回路 { if (union_set(e[i].u, e[i].v)) { sum += e[i].w;//如果纳入的边数等于顶点数-1,则说明最小生成树形成 if (++mst_edge == n - 1) { return sum; } } } return mst_edge; } int main() { int i, j, cost; while (scanf("%d", &n) != EOF) { ne = 0; for (i = 1; i <= n; ++i) { for (j = 1; j <= n; ++j) { scanf("%d", &cost); if (i != j) { e[ne].u = i; e[ne].v = j; e[ne++].w = cost; } } } printf("%d ", kruskal()); } return 0; }
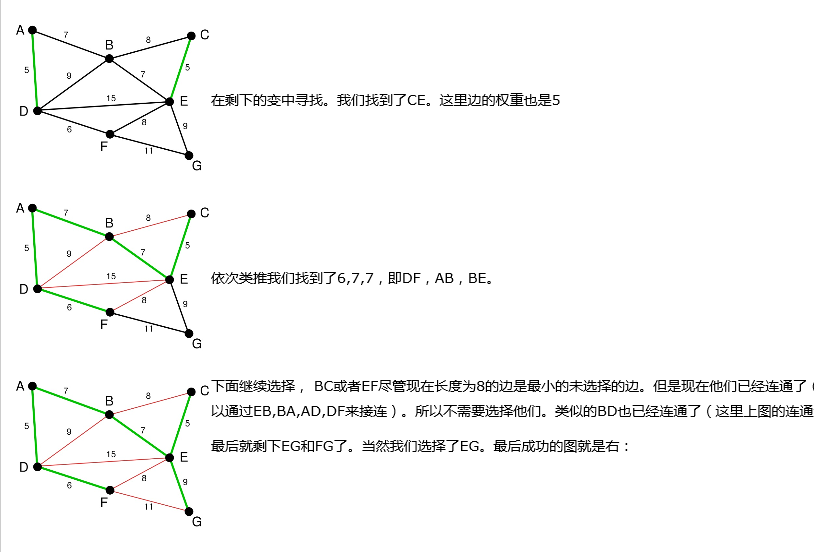
Kruskal算法图解