kruskal
1.基本思想(可忽略)
先构造一个只含 n 个顶点、而边集为空的子图,把子图中各个顶点看成各棵树上的根结点,之后,从网的边集 E 中选取一条权值最小的边,若该条边的两个顶点分属不同的树,则将其加入子图,即把两棵树合成一棵树,反之,若该条边的两个顶点已落在同一棵树上,则不可取,而应该取下一条权值最小的边再试之。依次类推,直到森林中只有一棵树,也即子图中含有 n-1 条边为止。
2.步骤(可忽略)
(1).新建图G,G中拥有原图中相同的节点,但没有边;
(2).将原图中所有的边按权值从小到大排序;
(3).从权值最小的边开始,如果这条边连接的两个节点于图G中不在同一个连通分量中,则添加这条边到图G中;
(4).重复3,直至图G中所有的节点都在同一个连通分量中。
3.证明(可忽略)
-
这样的步骤保证了选取的每条边都是桥,因此图G构成一个树。
-
为什么这一定是最小生成树呢?关键还是步骤3中对边的选取。算法中总共选取了n-1条边,每条边在选取的当时,都是连接两个不同的连通分量的权值最小的边
-
要证明这条边一定属于最小生成树,可以用反证法:如果这条边不在最小生成树中,它连接的两个连通分量最终还是要连起来的,通过其他的连法,那么另一种连法与这条边一定构成了环,而环中一定有一条权值大于这条边的边,用这条边将其替换掉,图仍旧保持连通,但总权值减小了。也就是说,如果不选取这条边,最后构成的生成树的总权值一定不会是最小的。
4.时间复杂度(可忽略)
平均时间复杂度为O(|E|log|E|),其中E和V分别是图的边集和点集。
题目
题目描述
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出orz
输入输出格式
输入格式:第一行包含两个整数N、M,表示该图共有N个结点和M条无向边。(N<=5000,M<=200000)
接下来M行每行包含三个整数Xi、Yi、Zi,表示有一条长度为Zi的无向边连接结点Xi、Yi
输出格式:输出包含一个数,即最小生成树的各边的长度之和;如果该图不连通则输出orz
输入输出样例
说明
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=20
对于40%的数据:N<=50,M<=2500
对于70%的数据:N<=500,M<=10000
对于100%的数据:N<=5000,M<=200000
样例解释:
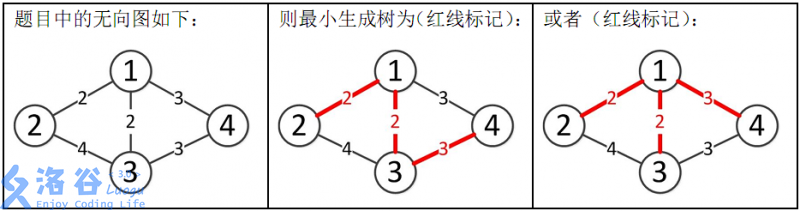
所以最小生成树的总边权为2+2+3=7
分析
以上我全部都是从百度上复制的,所以比较难懂,然而总的来说就是把一颗没有边的树,把权值小的边一个一个加上去而已,如果两个点已经在一个集合,那么不加上这条边。
题解
#include<iostream> #include<algorithm> using namespace std; int n,m,cnt,ans,fa[400005]; struct zxj{ int u,v,w;//u起点,v中点,w权值 }e[400005]; void init(){//每个的祖先都是自己 for(int i=1;i<=n;i++) fa[i]=i; } int find(int x){//寻找祖先 if(fa[x]==x) return x; return find(fa[x]); } void merge(int x,int y){//合并两个集合 x=find(x),y=find(y); if(x<y) fa[y]=x; else fa[x]=y; } bool cmp(zxj x,zxj y){//排序很重要,这样就可以得出最小的生成树 return x.w<y.w; } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=m;i++){ scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w); } init();//初始化 sort(e+1,e+m+1,cmp);//排序 for(int i=1;i<=m;i++){ if(find(e[i].u)!=find(e[i].v)){//如果两点不在一个集合 ans+=e[i].w;//加上权值 merge(e[i].u,e[i].v);//加上这条边(合并集合) cnt++;//边数+1 } if(cnt==n-1) break;//如果边数够,则停止循环 } printf("%d",ans); return 0; }