date: 2019-12-28
title: SC-EM
关于 EM 算法比较一般的形式可以参看以下的内容:
而这里我还是按照老师讲统计计算时候的思路进行笔记,可能和上述在形式上有一定的区别。
首先是算法要解决的问题,主要有两类:1. 存在删失数据 censored data (最典型的如医学上存活时间,或者是跟踪调查的时间,我们可能在一个时间点截止了,那么剩下的样本我们只知道其值大于一个数,但这个随机变量具体的取值我们不清楚),可分为左/右/双边删失;2. 隐变量 latent variables,我们无法观测到的变量,例如在 mixed model 中的混合系数(注意,我们必须要对这个变量有一定的了解,比如混合模型中成分的数量)。
一般情况下,我们希望用 MLE 对于参数进行估计,但在这两种情况下,我们没法得到似然函数的形式;然而,若我们把缺失/隐变量加入到模型中,似然函数的形式就明确下来了——然后,我们只需要使用期望将缺失/隐变量消去即可。
Idea: Reeplace a difficult likelihood maximization problem with a sequence of easier maximizations, where the limit of the sequence of maximizers is the solutions to the original one.
至于为什么 EM 算法是 iteration 的,之后会给出解释。
EM 算法
假设我们的观测为 (y) 我们希望得到的参数为 ( heta) ,即我们希望将下式最大化(简单起见我们已取对数):
因为其形式不好表达,我们利用条件概率公式转为
注意看此公式,左侧可理解为 complete 似然,而右侧为 observed 似然,以及 randomness (U|Y, heta) 。其中的 U 可理解为删失数据或隐变量。我们对两边取期望:
注意到,我们这里是对于 U 取期望,然而我们没有 U 的分布,因此我们利用观测 y 和上一步得到的 ( heta^*) 来近似 U 的分布(这也解释了为什么需要迭代求解)(注:这是我的粗浅的理解,但课上老师似乎对此不赞同,望 DL 指正)。这里就是 EM 算法总 E 的部分。需要注意的是:1. 我们感兴趣的是右侧的第一项对数似然,因为其较难求我们将转为对左式求 max;2. 注意式中的 ( heta) 和 ( heta^*) 是不同的,后者 U 的分布的参数,而前者是我们意欲求解的对象(为防止歧义,我特意将积分式写了出来)。
对(2)式分别取 ( heta) 和 ( heta^*) ,则我们有:
我们证明,后侧一项(>0)
在证明中,我们用到了 Jensen 不等式,即对于凹函数 (log) ,我们有(E[f(X)]le f(E(X))) ,在第二行中,我们根据期望的定义展开即可得到(注意式中的 ( heta) 和 ( heta^*) 是不同的,不能直接把条件往里代)。
于是,若有 (Q( heta, heta^*)>Q( heta^*, heta^*)),则 (l( heta)>l( heta^*))。当然,反过来不成立也就是说,只能保证是局部最优解,而无法保证全局最优。总结一下,对于最大化对数似然这个「hard」的问题,我们 reduced to iteratively (max Q( heta, heta^*)) , which is "easy"。
一个直观的解释:
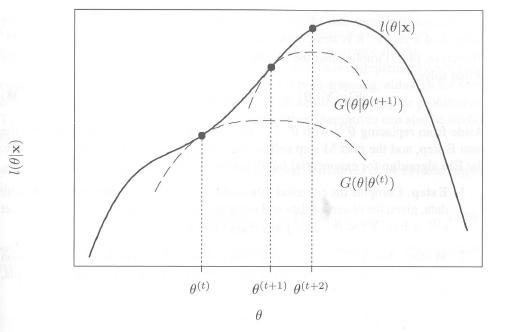
Steps
E-step: calculate (Q( heta, heta^*) = E_u[log f(y,u| heta)|Y=y, heta^*])
M-step: max ( heta^{(t+1)} = argmax _ heta Q( heta, heta^*))
Iterative until (|l( heta^{t+1})-l( heta^{t})|) or (|| heta^{(t+1)}- heta^{t}||over|| heta^{(t)}||) converges.
两个例子
第一个例子是 mixed model:我们考虑正态混合模型,
需要说明的是,对于混合参数 (pi_r) 我们是不了解的,但我们知道混合的数量 p,因此,参数( heta) 包含了混合参数和每一个的正态成分中的参数。我们定义随机变量 (U) 表示观测由哪一个成分生成。对于 EM 算法来说,最重要的就是求解似然函数和 U 的分布,我们先来表示一个观测时的分布:
这还不是最终的形式,我们先来看看 U 的分布 (U|Y, heta^*)
我们定义了权重函数 (w_r(y, heta^*)) 。另外注意这只是一个观测时的情况,我们给出 Q 的最终形式
注意到,相较于(3),我们除了给 y 加了角标求和之外,我们也把示性函数替换成了权重——这是因为,我们在(3)中仅给了在 U 取了一定定值时的情况,而若我们把 U 看做随机变量取期望,则可用上式的形式来表达。
这是 E-step,而在 M-step 中,对于右侧的第二个式子,我们代入正态分布的密度函数,求导即可;对于第一个式子,混合因子有约束 (sumpi_r=1),因此可用 Lagrange 方法求出最大值:
求导的 (pi_r=-{a_roverlambda}) ,又知 (sum a_r=n) ,因此
第二个例子是 censored data :模型为(N( heta,1))。假定我们的 observed 为 (X=(x_1,...,x_m,a...,a)) (把删失值记为 a,即观测 (ge a) ),complete data 为((x_1,...,x_m,z_{m+1},...,z_n)) 。
似然函数为
而 (Z|X, heta^*) 服从 trancated normal at level a from below
上为 E-step,对于 M-step,我们对 ( heta) 取导数
注意的,对于 trancated normal dist. 来说,其期望为 (E[z|X, heta^*]= heta^*+{phi(a- heta^*)over 1-Phi(a- heta^*)}) 。因此有更新公式
最终,给出一些 EM 算法的优缺点,课程网页上的内容老师也没讲,在此不多解释:
EM算法的优点
-
EM算法是数值稳定的, EM算法的每一次迭代会增加对数似然.
-
在非常一般的条件下, EM算法有可靠的全局收敛性, 即从参数空间的任何初始值出发, EM算法 一般总能收敛到对数似然函数的一个局部最大值点.
-
EM算法很容易实施,每一次迭代中的E步是对完全似然的期望, 而M步是完全数据的ML估计. 其经常 有closed form.
-
EM算法是容易进行程序设计的, 因其只涉及到似然函数, 而不需要其导数.
-
EM算法在计算机上实施时需要的存储空间很小, 其在每步迭代中不需要存储信息阵或者其导数等.
-
由于完全数据问题一般是一个标准问题, 因此在完全数据的MLE不存在显式解时, M步经常可以使用标准的统计方法来解决此问题. 一些扩展的EM算法就是基于此.
-
相比其他优化方法而言, EM算法需要的分析计算工作一般不太多, 其只要求完全对数似然的条件期望和最大化.
-
每一个迭代的成本是比较低的, 其抵消了EM算法需要很大迭代次数以达到收敛的不足之处.
-
通过监视每次迭代对数似然的单调性, 可以方便的监视收敛性和程序错误等.
-
EM算法可以用于对“缺失”值进行估计.
对EM算法的一些批评
-
不能自动给出参数估计的协方差矩阵的估计.
-
在一些看起来很简单的问题或者包含太多缺失信息的问题里, EM算法可能收敛很慢.
-
当存在多个极值点时, EM算法不能保证收敛到全局最大值点, 此时, 收敛到的极值点依赖于初始值.
-
在一些问题里, EM算法需要的E步或者M步可能不能给出分析解.