opengl 学习 之 17 lesson
简介
这个教程有点超出了opengl的范围了,但是解决了一个非常公共的问题:如何去表示旋转?
在第3个教程,我们学会了矩阵可以表示一个点绕着一个特定的轴旋转。当矩阵是一个整洁的方式去旋转点,处理矩阵十分坤丹:举个例子,从最终的矩阵获取旋转轴十分困难。
我们将用两种方式表示旋转:欧拉角和四元素。最重要的是,我们将会解释为什么你需要尽可能的使用四元素(可能欧拉家有万向锁,以前看过部分相关知识)。
link
http://www.opengl-tutorial.org/uncategorized/2017/06/07/website-update/
http://www.opengl-tutorial.org/cn/intermediate-tutorials (还有中文版在一直没有察觉)
https://zhuanlan.zhihu.com/p/144025113 (知乎大佬)
引言:旋转 VS 朝向
方向就是一种状态:“物体的朝向是?“
一个旋转是一个操作:“应用这个旋转于物体”
当你应用一个旋转,你改变物体的方向。
欧拉角(Euler Angles)
欧拉角是最方便的方式去表示一个朝向。你通常存储三个旋转绕着XYZ轴。很容易领会,你可以使用一个vec3存储他
vec3 EulerAngles( RotationAroundXInRadians, RotationAroundYInRadians, RotationAroundZInRadians);
通常游戏角色不会在x和z轴上旋转,只会在垂直轴上旋转(Y轴?)
另一个比较好应用欧拉角的地方是FPS摄像头,你有一个叫对于heading(Y),一个对于摄像头的up/down(x).
欧拉角的缺点
- 在两个方向之间进行平滑过渡是十分困难的。直接的差值xyz轴的旋转角度,会很难看。
- 应用很多个旋转是复杂的和不精确的:你必须计算最终旋转矩阵,和猜测欧拉角从矩阵中。
- 一个总所周知的问题是万向锁。会让你的旋转锁定和其他的奇异点会翻转你的模型朝向。
- 不同的角度产生相同的旋转(-180° 和180°产生相同的旋转)
- 比较混乱,xyz轴旋转的顺序不同导致的转换混乱。
- 操作复杂,旋转N°绕着一个特定的轴。
四元素可以解决以上一切问题哦。
Quaternions(四元数)
一个四元数表示四个数字[x y z w],表示旋转用一下的方式:
// RotationAngle is in radians
x = RotationAxis.x * sin(RotationAngle / 2)
y = RotationAxis.y * sin(RotationAngle / 2)
z = RotationAxis.z * sin(RotationAngle / 2)
w = cos(RotationAngle / 2)
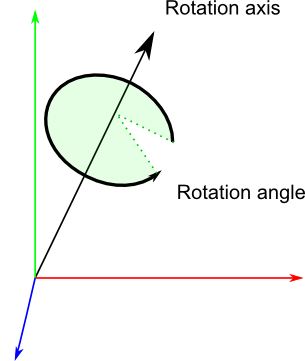
旋转轴和旋转角上图解释的很清楚了。
所以本质上四元素存储着一个旋转轴和一个旋转角,
读取四元数
这种格式不如欧拉角只管,但是仍然刻度读取:xyz表示旋转轴,w表示acos(旋转角)/2。举个例子,想象你看到之后的值在debugger:[0.7 0 0 0.7]. x = 0.7 ,大部分的旋转绕着X轴; 2 * acos(0.7)=1.59 radians,旋转90度。
基础的操作
在C++中创建一个四元素
// Don't forget to #include <glm/gtc/quaternion.hpp> and <glm/gtx/quaternion.hpp>
// Creates an identity quaternion (no rotation)
quat MyQuaternion;
// Direct specification of the 4 components
// You almost never use this directly
MyQuaternion = quat(w,x,y,z);
// Conversion from Euler angles (in radians) to Quaternion
vec3 EulerAngles(90, 45, 0);
MyQuaternion = quat(EulerAngles);
// Conversion from axis-angle
// In GLM the angle must be in degrees here, so convert it.
MyQuaternion = gtx::quaternion::angleAxis(degrees(RotationAngle), RotationAxis);
在GLSL中创建一个四元数
自己封装一个
转化一个四元数到矩阵
mat4 RotationMatrix = quaternion::toMat4(quaternion);
你可以用这个来构建你的M矩阵
mat4 RotationMatrix = quaternion::toMat4(quaternion);
...
mat4 ModelMatrix = TranslationMatrix * RotationMatrix * ScaleMatrix;
// You can now use ModelMatrix to build the MVP matrix
So,你改如何选择呢?
在3D引擎中你要是用四元数,但是对于GUI使用者你需要使用欧拉角,因为直观。
一般的共识是,在内部使用四元数实现所有,但是在外部暴露出欧拉角接口。
我如何的值两个四元数是相同的呢?
使用向量,如果两个的点积表示两个夹角的余弦值。如果这个值是1,那么这两个四元数的朝向是相似的。
float matching = quaternion::dot(q1, q2);
if ( abs(matching-1.0) < 0.001 ){
// q1 and q2 are similar
}
你可以也得到角度这q1和q2之间使用acos。
我如何应用一个旋转对于一个点
你可以做
rotated_point = orientation_quaternion * point;
注意旋转的中心总是原点,如果你想绕另一个点旋转:
rotated_point = origin + (orientation_quaternion * (point-origin));
我如何插值在两个四元数之间?
称为:球形线性差值 SLERP:Spherical Linear intERPolation.
glm::quat interpolatedquat = quaternion::mix(quat1, quat2, 0.5f); // or whatever factor
如何累积两个旋转
quat combined_rotation = second_rotation * first_rotation;
我如何找到两个向量之间的旋转
换句话说,如何从v1向量转到v2向量,这里的向量表示空间中的向量
基本的思想很直接
- 两个向量之间的教教很容易找到:点积
- 需要的旋转轴很容易找到:两个向量之间的叉积
下面的算法做这些
quat RotationBetweenVectors(vec3 start, vec3 dest){
start = normalize(start);
dest = normalize(dest);
float cosTheta = dot(start, dest);
vec3 rotationAxis;
if (cosTheta < -1 + 0.001f){
// special case when vectors in opposite directions:
// there is no "ideal" rotation axis
// So guess one; any will do as long as it's perpendicular to start
rotationAxis = cross(vec3(0.0f, 0.0f, 1.0f), start);
if (gtx::norm::length2(rotationAxis) < 0.01 ) // bad luck, they were parallel, try again!
rotationAxis = cross(vec3(1.0f, 0.0f, 0.0f), start);
rotationAxis = normalize(rotationAxis);
return gtx::quaternion::angleAxis(glm::radians(180.0f), rotationAxis);
}
rotationAxis = cross(start, dest);
float s = sqrt( (1+cosTheta)*2 );
float invs = 1 / s;
return quat(
s * 0.5f,
rotationAxis.x * invs,
rotationAxis.y * invs,
rotationAxis.z * invs
);
}
我如何使用朝向,但是限制旋转在一定的速度?
基础的想法是 SLERP 球形线性差值,设定一个插值值,让角度不大于想要的值:
float mixFactor = maxAllowedAngle / angleBetweenQuaternions;
quat result = glm::gtc::quaternion::mix(q1, q2, mixFactor);
更复杂的实现可以处理一些特殊的情况
quat RotateTowards(quat q1, quat q2, float maxAngle){
if( maxAngle < 0.001f ){
// No rotation allowed. Prevent dividing by 0 later.
return q1;
}
float cosTheta = dot(q1, q2);
// q1 and q2 are already equal.
// Force q2 just to be sure
if(cosTheta > 0.9999f){
return q2;
}
// Avoid taking the long path around the sphere
if (cosTheta < 0){
q1 = q1*-1.0f;
cosTheta *= -1.0f;
}
float angle = acos(cosTheta);
// If there is only a 2° difference, and we are allowed 5°,
// then we arrived.
if (angle < maxAngle){
return q2;
}
float fT = maxAngle / angle;
angle = maxAngle;
quat res = (sin((1.0f - fT) * angle) * q1 + sin(fT * angle) * q2) / sin(angle);
res = normalize(res);
return res;
}
简单的使用方法
CurrentOrientation = RotateTowards(CurrentOrientation, TargetOrientation, 3.14f * deltaTime );
code
#include <glm/gtc/quaternion.hpp>
#include <glm/gtx/quaternion.hpp>
#include <glm/gtx/euler_angles.hpp>
#include <glm/gtx/norm.hpp>
using namespace glm;
#include "quaternion_utils.hpp"
// Returns a quaternion such that q*start = dest
quat RotationBetweenVectors(vec3 start, vec3 dest){
start = normalize(start);
dest = normalize(dest);
float cosTheta = dot(start, dest);
vec3 rotationAxis;
if (cosTheta < -1 + 0.001f){
// special case when vectors in opposite directions :
// there is no "ideal" rotation axis
// So guess one; any will do as long as it's perpendicular to start
// This implementation favors a rotation around the Up axis,
// since it's often what you want to do.
rotationAxis = cross(vec3(0.0f, 0.0f, 1.0f), start);
if (length2(rotationAxis) < 0.01 ) // bad luck, they were parallel, try again!
rotationAxis = cross(vec3(1.0f, 0.0f, 0.0f), start);
rotationAxis = normalize(rotationAxis);
return angleAxis(glm::radians(180.0f), rotationAxis);
}
// Implementation from Stan Melax's Game Programming Gems 1 article
rotationAxis = cross(start, dest);
float s = sqrt( (1+cosTheta)*2 );
float invs = 1 / s;
return quat(
s * 0.5f,
rotationAxis.x * invs,
rotationAxis.y * invs,
rotationAxis.z * invs
);
}
// Returns a quaternion that will make your object looking towards 'direction'.
// Similar to RotationBetweenVectors, but also controls the vertical orientation.
// This assumes that at rest, the object faces +Z.
// Beware, the first parameter is a direction, not the target point !
quat LookAt(vec3 direction, vec3 desiredUp){
if (length2(direction) < 0.0001f )
return quat();
// Recompute desiredUp so that it's perpendicular to the direction
// You can skip that part if you really want to force desiredUp
vec3 right = cross(direction, desiredUp);
desiredUp = cross(right, direction);
// Find the rotation between the front of the object (that we assume towards +Z,
// but this depends on your model) and the desired direction
quat rot1 = RotationBetweenVectors(vec3(0.0f, 0.0f, 1.0f), direction);
// Because of the 1rst rotation, the up is probably completely screwed up.
// Find the rotation between the "up" of the rotated object, and the desired up
vec3 newUp = rot1 * vec3(0.0f, 1.0f, 0.0f);
quat rot2 = RotationBetweenVectors(newUp, desiredUp);
// Apply them
return rot2 * rot1; // remember, in reverse order.
}
// Like SLERP, but forbids rotation greater than maxAngle (in radians)
// In conjunction to LookAt, can make your characters
quat RotateTowards(quat q1, quat q2, float maxAngle){
if( maxAngle < 0.001f ){
// No rotation allowed. Prevent dividing by 0 later.
return q1;
}
float cosTheta = dot(q1, q2);
// q1 and q2 are already equal.
// Force q2 just to be sure
if(cosTheta > 0.9999f){
return q2;
}
// Avoid taking the long path around the sphere
if (cosTheta < 0){
q1 = q1*-1.0f;
cosTheta *= -1.0f;
}
float angle = acos(cosTheta);
// If there is only a 2?difference, and we are allowed 5?
// then we arrived.
if (angle < maxAngle){
return q2;
}
// This is just like slerp(), but with a custom t
float t = maxAngle / angle;
angle = maxAngle;
quat res = (sin((1.0f - t) * angle) * q1 + sin(t * angle) * q2) / sin(angle);
res = normalize(res);
return res;
}
void tests(){
glm::vec3 Xpos(+1.0f, 0.0f, 0.0f);
glm::vec3 Ypos( 0.0f, +1.0f, 0.0f);
glm::vec3 Zpos( 0.0f, 0.0f, +1.0f);
glm::vec3 Xneg(-1.0f, 0.0f, 0.0f);
glm::vec3 Yneg( 0.0f, -1.0f, 0.0f);
glm::vec3 Zneg( 0.0f, 0.0f, -1.0f);
// Testing standard, easy case
// Must be 90?rotation on X : 0.7 0 0 0.7
quat X90rot = RotationBetweenVectors(Ypos, Zpos);
// Testing with v1 = v2
// Must be identity : 0 0 0 1
quat id = RotationBetweenVectors(Xpos, Xpos);
// Testing with v1 = -v2
// Must be 180?on +/-Y axis : 0 +/-1 0 0
quat Y180rot = RotationBetweenVectors(Xpos, Xneg);
// Testing with v1 = -v2, but with a "bad first guess"
// Must be 180?on +/-Y axis : 0 +/-1 0 0
quat X180rot = RotationBetweenVectors(Zpos, Zneg);
}
TIPS
glm库默认使用弧度制了。有一些接口挺好用的
#define DEGTORAD M_PI/double(180.0)
glm::vec3 ou = eulerAngles(inq); // 一个四元数转为欧拉角
glm::quat inq = inAngleAxis(axiss, angle); // 输入 旋转轴和旋转角度产生一个四元数
quat common::inAngleAxis(vec3 RotationAxis, double RotationAngle) {
RotationAngle = RotationAngle * DEGTORAD;// 角度转弧度
RotationAxis = normalize(RotationAxis);
quat t;
t.x = RotationAxis.x * sin(RotationAngle / 2);
t.y = RotationAxis.y * sin(RotationAngle / 2);
t.z = RotationAxis.z * sin(RotationAngle / 2);
t.w = cos(RotationAngle / 2);
return t;
}
Point3D common::rotateByQuatToCenter(const quat& q, const Point3D& in, const Point3D& center) { // 输入顶点和一个四元数,让这个顶点绕着中心点旋转
glm::mat4 model = glm::mat4(1.0f);
model = glm::mat4_cast(q) * model; // 旋转模型矩阵
vec4 p00(in.x - center.x, in.y - center.y, in.z - center.z, 0);
vec4 out = model * p00;
Point3D ou;
ou.x = out.x + center.x;
ou.y = out.y + center.y;
ou.z = out.z + center.z;
return ou;
}