壹 ❀ 引
在前两篇排序文章中,我们分别介绍了冒泡排序与选择排序,趁热打铁,我们接着聊插入排序。老实说,在分析排序过程中头脑很清楚,过后再尝试写出排序代码还有点坎坷...可能是我脑瓜子不太机灵的问题,不过我相信多练习对于算法的感觉会好起来,那么让我们开始。
贰 ❀ 插入排序基本概念
插入排序与我们生活中打扑克牌斗地主的原理相同,在分完手牌后,拿起来就是一堆乱序的牌组,接下来我们总是会一一把排序不对的牌抽出来,并插入到它应该在的位置,那么这个调整牌组顺序的过程就是在做插入排序。只是打扑克时,我们总是会站在宏观视角,以最便捷的方式把牌调整好,而程序不同,它得按照一个逻辑一步步调整,大家明白这个意思就好。
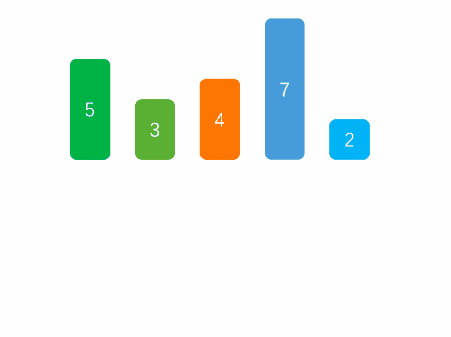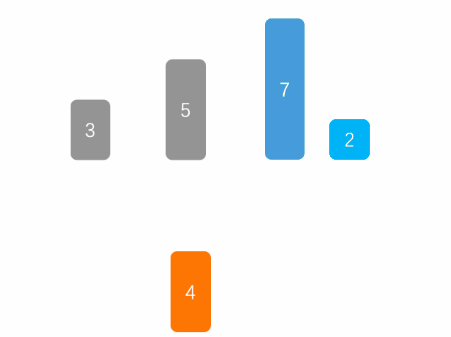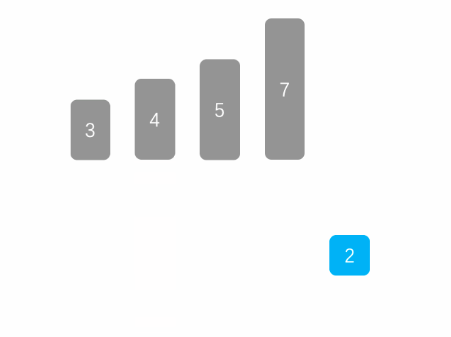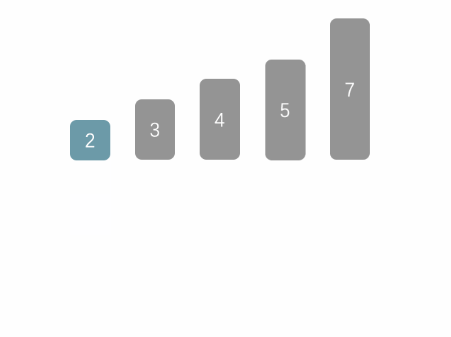
插入排序主要按照如下步骤运转:
- 将数组中的第一个元素看成有序序列,也就是最初的参照点,把从第二个元素到尾部所有元素都看成未排序序列。
- 开始遍历未排序序列,将每个未排序元素插入到有序序列中它应该的位置,如果未排序元素与有序序列中某个元素相同,则将其放到有序序列该元素后面。
我们来看个简单的例子,假设现在有数组[4,2,1,3];
现在4是有序序列,2,1,3为无序序列,开始遍历。
- 无序序列第1次遍历
- 有序序列第1次遍历
- 2与4比较,因为2更小,2与4互换位置,此时有序序列为
2,4,无序序列为1,3。
- 2与4比较,因为2更小,2与4互换位置,此时有序序列为
- 有序序列第1次遍历
- 无序序列第2次遍历
- 有序序列第1次遍历
- 1比4小,互换位置,此时有序序列为
2,1,4,无序序列为3。
- 1比4小,互换位置,此时有序序列为
- 有序序列第2次遍历
- 1比2小,互换位置,此时有序序列为
1,2,4,无序序列为3。
- 1比2小,互换位置,此时有序序列为
- 有序序列第1次遍历
- 无序序列第3次遍历
- 有序序列第1次遍历
- 3比4小,互换位置,此时有序序列为
1,2,3,4,排序完成。
- 3比4小,互换位置,此时有序序列为
- 有序序列第1次遍历
通过上述分析,我们大致可以得到这样几个结论:
- 数组遍历必定是从i=1处开始。
- 每次遍历我们都会拿一个无序序列的元素和有序序列元素进行比较,有序序列可能存在多个,所以需要循环嵌套。
知道了这些,我们来尝试实现代码。
叁 ❀ 插入排序实现
function insertionSort(arr) {
var len = arr.length,
preIndex;
// 无序序列从i=1处开始遍历
for (var i = 1; i < len; i++) {
// 记录上一个值的索引
preIndex = i - 1;
// 如果上一个值比当前值大,互换位置,考虑有序序列可能有多个,所以需要让preIndex递减
while (preIndex >= 0 && arr[preIndex] > arr[preIndex + 1]) {
arr[preIndex] = [arr[preIndex + 1], arr[preIndex + 1] = arr[preIndex]][0];
preIndex--;
};
};
return arr;
};
var arr = [4, 2, 1, 3];
insertionSort(arr); //[1, 2, 3, 4]
当然我这个实现看着可能不太好看,不过我个人感觉更好理解一点,下面是偏官方的插入排序实现:
function insertionSort(arr) {
var len = arr.length;
var preIndex, current;
for (var i = 1; i < len; i++) {
preIndex = i - 1;
current = arr[i];
while (preIndex >= 0 && arr[preIndex] > current) {
arr[preIndex + 1] = arr[preIndex];
preIndex--;
};
arr[preIndex + 1] = current;
};
return arr;
};
与我的实现不同地方在于,它不是每次对比后直接交换位置,而是用当前值一直和上一个比,满足条件就修改当前值,由于preIndex一直递减,所以当前值一直在变,一直比完为止,最后设置数组0项为当前值,而此时的当前值一定是有序序列中最小的一个。比较巧妙,不过从记忆角度上来说,我可能有些记不住....因人而异了。
那么关于插入排序就说到这里,文中如果存在描述不当还望指出,本文结束。