壹 ❀ 引
题目来自LeetCode的525. 连续数组,难度中等,题目描述如下:
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。
示例 1:
输入: nums = [0,1] 输出: 2 说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。示例 2:
输入: nums = [0,1,0] 输出: 2 说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。提示:
1 <= nums.length <= 105
nums[i] 不是 0 就是 1
贰 ❀ 题解分析
根据题意,要求其实是给定我们一个数组,数组元素只包含0或者1,而我们需要找到0和1数量相等的最长子数组。比如例子1中,0和1各有1个,因此子数组长度就是2。而在例子二中,不管是[0,1]还是[1,0]都满足条件,但不管选谁,长度还是2,所以最终得到的结果还是2。
有次我们可以推测,数组中可能会存在多段满足条件的子数组,因此求解时一定会用到Math.max用于找出满足条件的最大子数组长度。
让我们将问题抽象化,题目要求是找到拥有包含相同数量1与0的子数组,如下数组起始都满足条件,且长度为4。
[1,1,0,0]
[1,0,1,0]
我们在现实生活中,应该都遇到过这样类似的操作,我们在一个空的输入框打了2个数字,ctrl+z撤销2次,于是内容又回到了最初的样子。我们将一个魔方扭转了2次后,又回退刚才操作2次,于是魔方又变成了最初的样子,操作前与操作结束后,事物的状态相同。
对应到上述数组中,[1,1,0,0]可以理解为连续输入两次数字,紧接着又撤销了2次。数组[1,0,1,0]可以理解为先输入一个数字,紧接着撤销,又输入一个数字后又撤销,不管我们输入顺序如何,事物又回归到了原有的样子。
那我们是不是可以这样理解,一开始有个数字0,遇到1我们就加个1,遇到0我们就减去1,像上述两种数组,你会发现最终结果都是0。我们可以将数组中的0都转为-1,将问题演变为元素和为0的最长子数组问题。
说到求子数组元数和,不得不提前缀和的概念,还记得我在JS LeetCode 303. 区域和检索 - 数组不可变,一维数组的前缀和一文中,提到了前缀和概念,我们简单复习下。
假设给定数组[1,1,1,1]以及两个下标j k j<k,现在要你求j到k的所有数字的和,怎么做呢?我们当然可以根据这两个下标把对应的数字依次累加从而得到结果,这没问题,但如果我们要求很多个范围的和,这个数组也很大,每次都得从头开始累加就特别耗时了,有没有什么办法能从O(1)的时间复杂度直接得到结果,这就需要利用到前缀和。
假设我们有一个前缀和数组preSum,它和原数组的对应关系如下,也就是说我们通过一次遍历,已经知道了从下标0到每个下标 i 的元素和
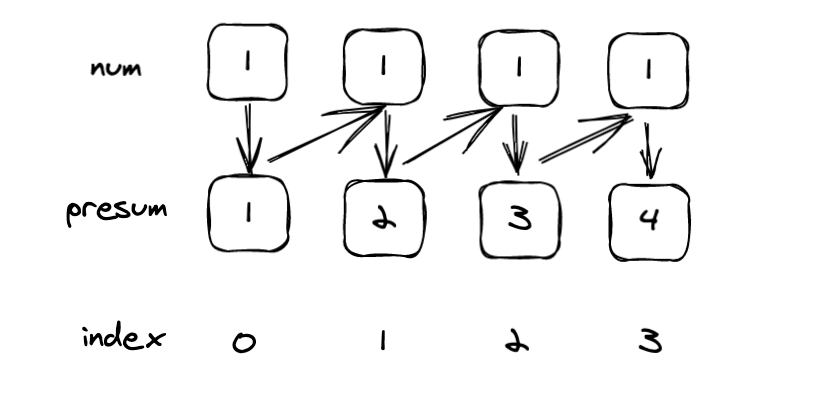
那么现在,我们要知道下标1到下标3的元素和,扳指头都知道结果是3,但是站在presum的角度,其实我们可以知道是presum[3]-presum[0],从而我们可以得到一个结论,要求任意j到k的元素和,其结果为presum[k]-presum[j-1]。
还记得我们前面对于题目的转换吗?我们现在就是要找到一个子数组其元素和为0,那么由此可以推导为presum[k]-presum[j-1]=0,再次转换也就是presum[k] = presum[j-1]。意识到了什么没?当我们遍历一次数组,其实可以得到各种前缀和的情况,而现在我们就是要找到一个前缀和的数字出现2次的情况,只要一个和能出现两次,那么它们之间的区间的数字和一定等于0,也就是1和0出现的次数频率相等。为了方便理解,我们来看个最简单的例子:
[1,0]
//转变为
[1,-1]
我们假设前缀和初始值是0,且它的下标为-1,上面的数组对应关系是:

如上图,这个数组的前缀和演变中,0出现了2次,那么符合条件的子数组其实就是下标-1到1之间的元素,长度是多少呢?其实就是第二个0的小标1减去上一个0的下标-1,也就是2。
我们再来看个例子,比如数组[1,1,1,0],转为-1后其实就是[1,1,1,-1]。让我们看下计算过程:
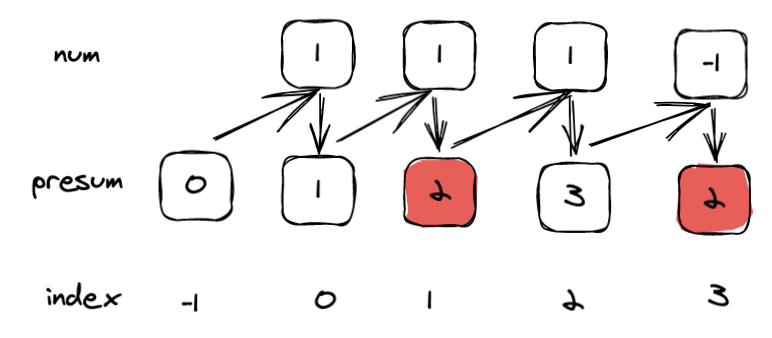
你会发现这个例子满足条件的数组长度是3-1=2,其实说到底,还记得文章开头我们所说的事物的状态吗?一个魔方一开始被打断,然后又通过回退还原成最初的样子,两个状态之间必然包含了相同的打乱次数和回退次数,那么我们只要找到相同的两个状态,自然就知道期间有多少满足条件的数字了。
当然,可能会存在多对相同的状态,因此我们前面也说了,需要找出长度最长的满足条件的子数组。
我们可以借用map,定义一个k为0,val为-1作为初始值,这里的k就是子数组的前缀和,而val是出现这个前缀和时当前所在的索引,让我们实现这段代码:
/**
* @param {number[]} nums
* @return {number}
*/
var findMaxLength = function (nums) {
// 我们将数组中的0转为-1
for (let i = 0; i < nums.length; i++) {
if (nums[i] === 0) {
nums[i] = -1;
};
};
// 初始我们能拿到符合条件子数组的长度
let maxLength = 0;
// 用于求前缀和的初始值
let sum = 0;
let map = new Map();
map.set(0, -1);
for (let i = 0; i < nums.length; i++) {
sum += nums[i];
// 当前有这个前缀和的值了吗?
if (map.has(sum)) {
// 有了,那就计算他们之前的索引差,就是符合条件的子数组长度
maxLength = Math.max(maxLength, i - map.get(sum));
} else {
// 没有,那就记录这个前缀和出现的索引
map.set(sum, i);
};
};
return maxLength;
};
当我们理解了状态的变化,其实我们完全没必要做把0变成-1的操作,遇到1自增,遇到0自减一个1其实也能达到同样的效果:
/**
* @param {number[]} nums
* @return {number}
*/
var findMaxLength = function (nums) {
// 初始我们能拿到符合条件子数组的长度
let maxLength = 0;
// 用于求前缀和的初始值
let sum = 0;
let map = new Map();
map.set(0, -1);
for (let i = 0; i < nums.length; i++) {
if (nums[i]) {
sum += 1;
} else {
sum -= 1;
};
// 当前有这个前缀和的值了吗?
if (map.has(sum)) {
// 有了,那就计算他们之前的索引差,就是符合条件的子数组长度
maxLength = Math.max(maxLength, i - map.get(sum));
} else {
// 没有,那就记录这个前缀和出现的索引
map.set(sum, i);
};
};
return maxLength;
};
OK,那么本题的分析就到这里了。