壹 ❀ 引
本题来自LeetCode 852. 山脉数组的峰顶索引,难度依旧是简单,也是一道考二分法的题目,题目描述如下:
符合下列属性的数组 arr 称为 山脉数组 :
arr.length >= 3
存在 i(0 < i < arr.length - 1)使得:
arr[0] < arr[1] < ... arr[i-1] < arr[i]
arr[i] > arr[i+1] > ... > arr[arr.length - 1]
给你由整数组成的山脉数组 arr ,返回任何满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i + 1] > ... > arr[arr.length - 1] 的下标 i 。示例 1:
输入:arr = [0,1,0] 输出:1示例 2:
输入:arr = [0,2,1,0] 输出:1示例 3:
输入:arr = [0,10,5,2] 输出:1示例 4:
输入:arr = [3,4,5,1] 输出:2示例 5:
输入:arr = [24,69,100,99,79,78,67,36,26,19] 输出:2提示:
3 <= arr.length <= 104
0 <= arr[i] <= 106
题目数据保证 arr 是一个山脉数组
贰 ❀ 暴力解法
根据题目,我们会得到一个代表峰顶高度的山脉数组,每一个数字都可以表示一座山峰的高度,而题目要求就是要找到某个山峰数,满足它左侧的山都比它低,同时满足它右侧的山也都比它低,返回这个山脉的索引。
我一想,这难道不就是要找到数组最大值的索引吗?毕竟数组最大数的左右两侧注定会都小于它,盘它:
var peakIndexInMountainArray = function(arr) {
// 找到最大数的索引?
let max = Math.max(...arr);
return arr.indexOf(max);
};
直接点击提交,这个思路还真给过了。但从时间复杂度来说,假设最高的山峰是数组最后一位,最坏的情况就是O(n)。
叁 ❀ 二分法思路
OK,让我们在看看二分法的思路。其实题目要求有点没说清,所谓保证arr是一个山脉数组,其实意思就是一定是个数字先升后降低的数组,啥意思呢?山脉数组是图1这样的,而不是图2这样的:

所以像[1,2,1],[1,2,3,5,4,1]这种都是山脉数组,它只有一个山峰,只有一个最高点。而像[1,2,1,2]这类数组就都不是山脉数组,很明显它存在了多个山峰。
因此我们假定取数组中间数mid,它存在三种情况。
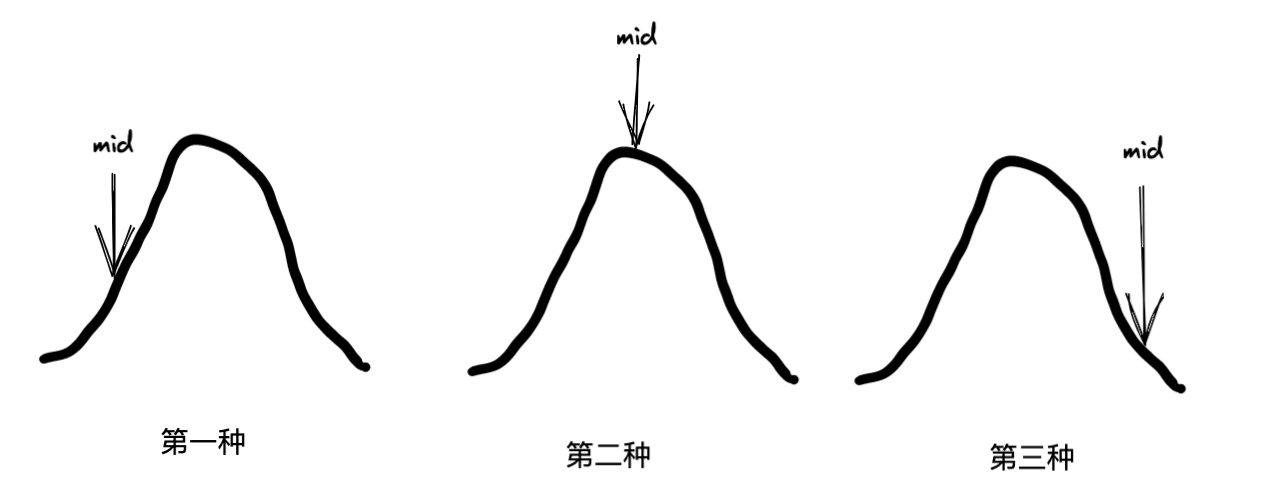
第一种,在上升区域,此时arr[mid]<arr[mid+1],那说明最高峰肯定还没到啊,所以此时应该调整左边界,让l=mid+1,为什么加1?因为不可能是mid啊,不需要考虑它了,直接跳过加个1。
第二种,好巧不巧,正好mid是山顶,那么此时arr[mid]>arr[mid+1],且arr[mid]>arr[mid-1]。
第三种,取在了下坡区域,此时满足arr[mid]>arr[mid+1]。但是很明显此时mid并不是最高,结合第二种,综合发现当arr[mid]>arr[mid+1]时,它可能是最高,也可能最高还在左侧,保险起见,此时应该调整右边界,也就是r = mid。为什么不减1?因为可能是第二种情况啊,减1直接好家伙,把山峰给排除了。
所以结合来说,我们只需要根据第二种跳出循环,其余情况不断调整左右边界,最后一定会找到符合条件的数字,题目不是都说了,一定是个山脉数组,所以直接实现代码:
var peakIndexInMountainArray = function (arr) {
// 定义左右边界
let l = 0, r = arr.length - 1;
// 这里不用加=,因为指针还没重合前一定会找到最高的山峰
while (l < r) {
let mid = Math.floor(l + (r - l) / 2);
// 如果是第二种情况,直接跳出循环
if (arr[mid] > arr[mid + 1] && arr[mid] > arr[mid - 1]) {
return mid;
};
// 二 三种情况,跳转右边界
if (arr[mid] > arr[mid + 1]) {
r = mid;
} else {
// 反之调整左边界
l = mid + 1;
}
}
};
应该很清晰了,本题结束。