
two parts:
1, task represented by DAG
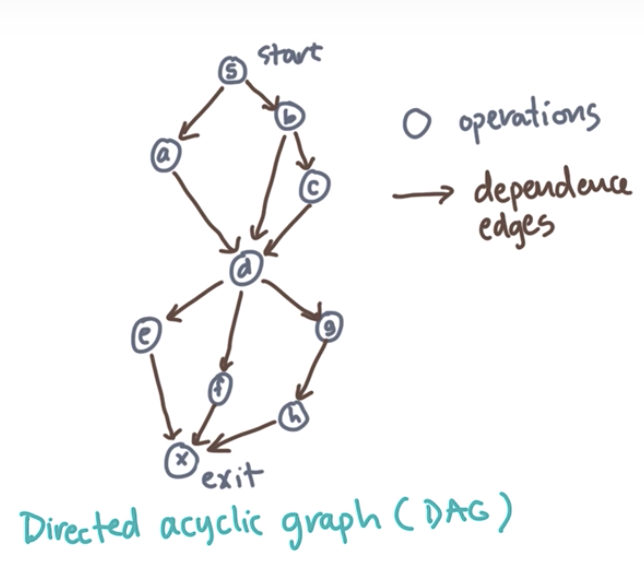
edges << operations => better for parallelism
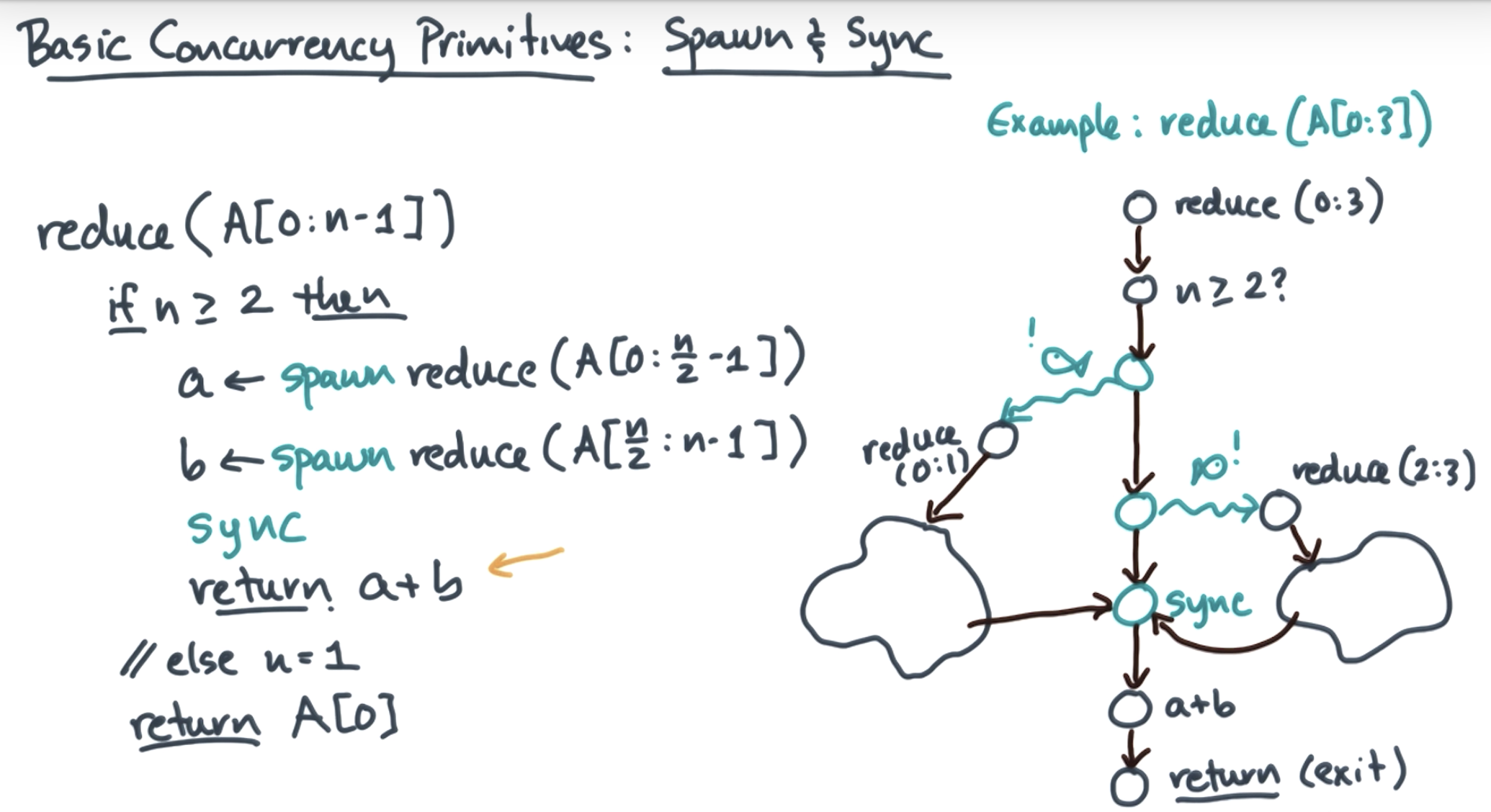
2, programming model defining DAG



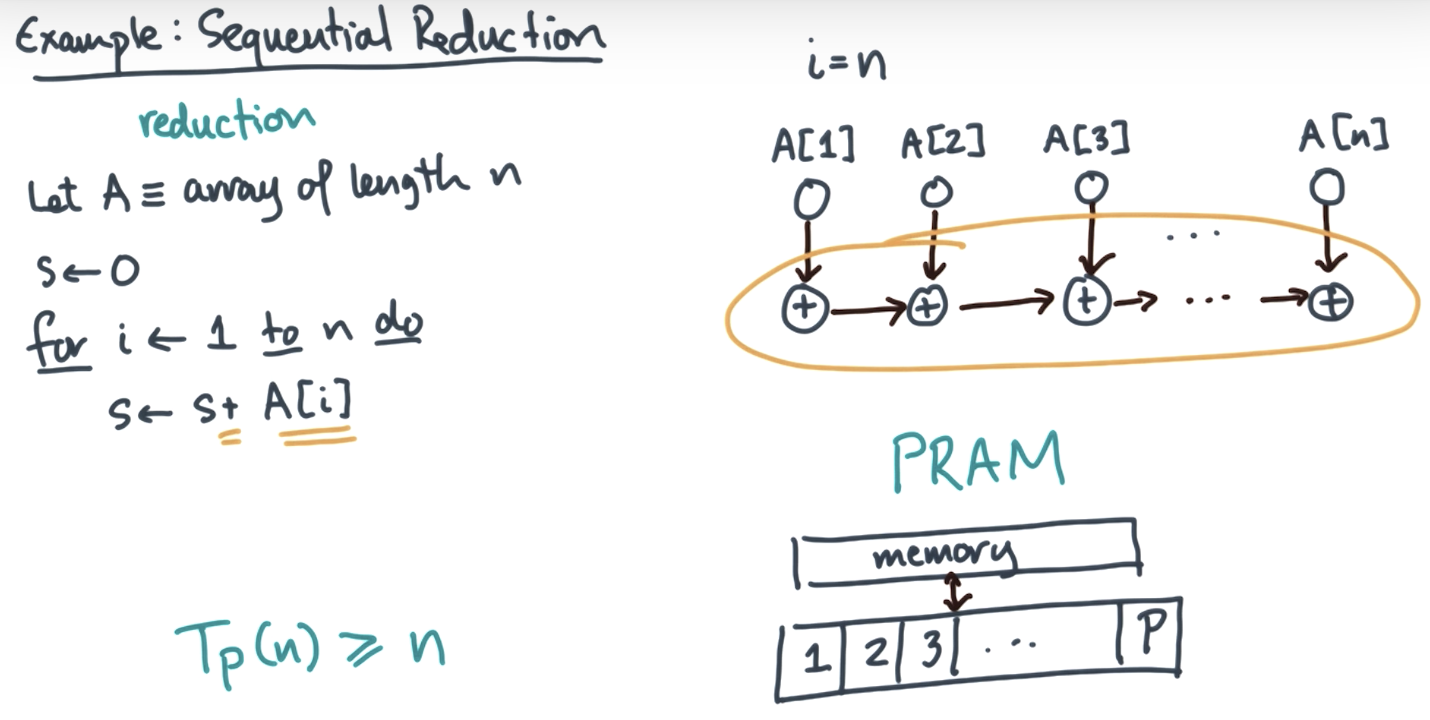
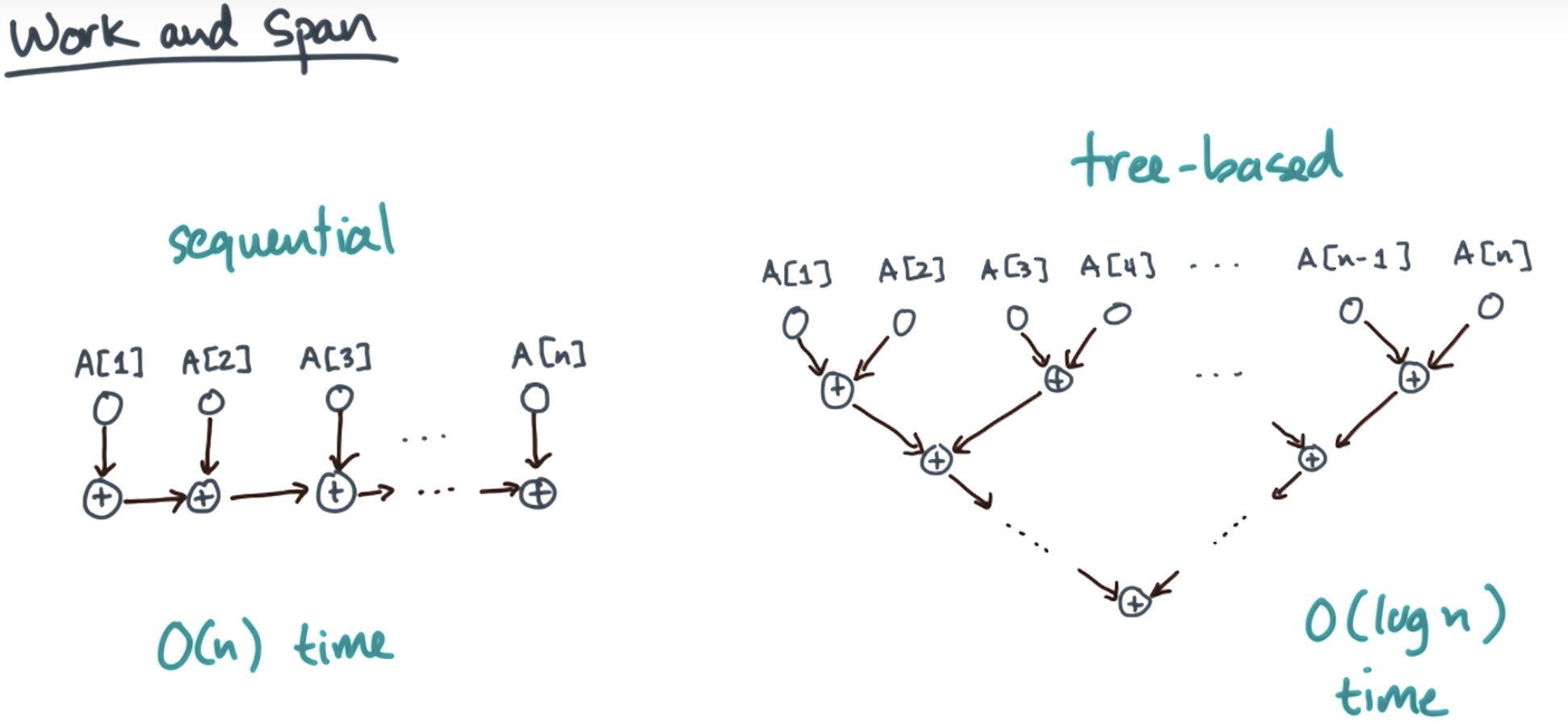
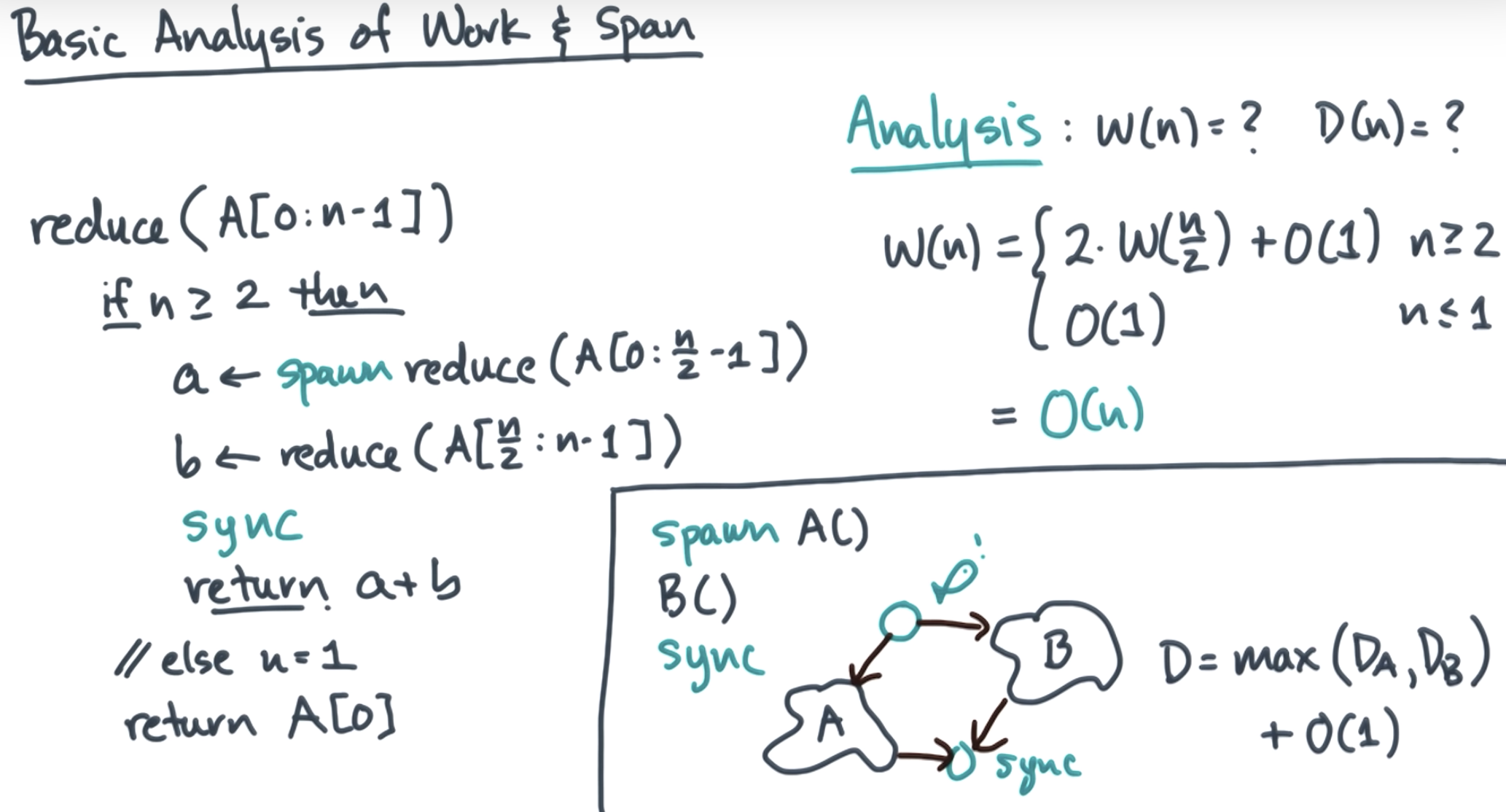
work span analysis


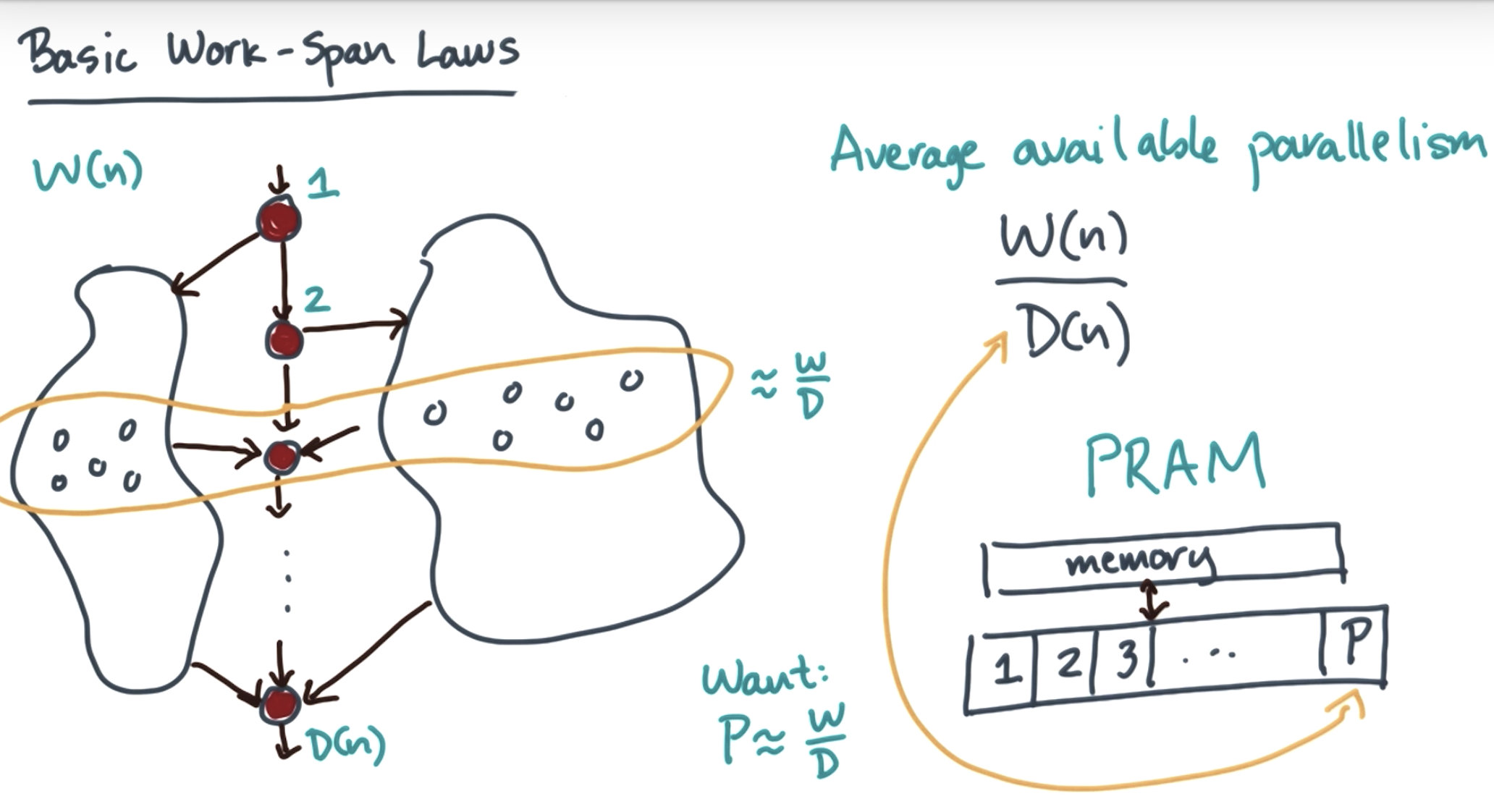


https://maths-people.anu.edu.au/~brent/pub/pub022.html


second condition
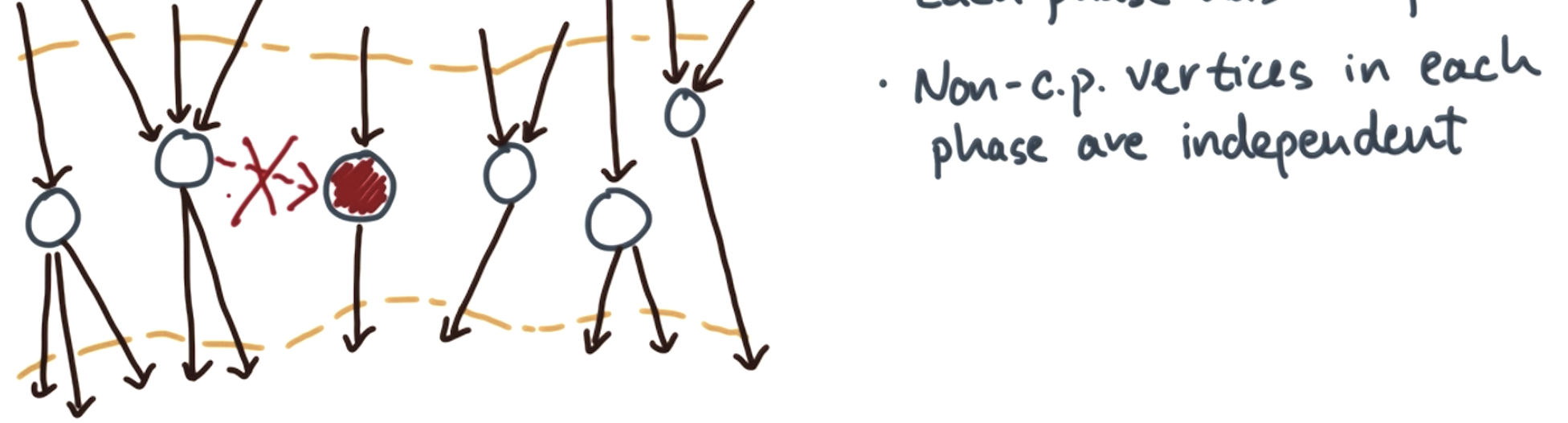

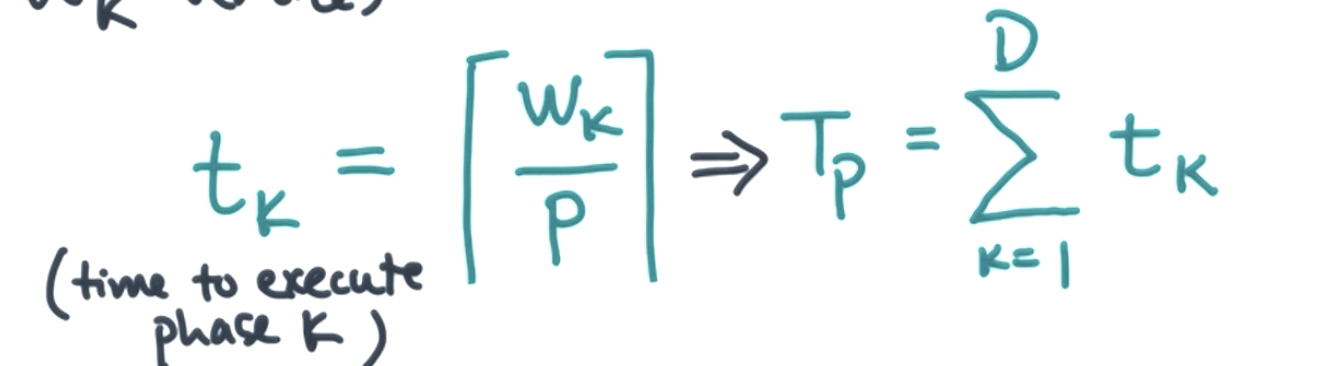
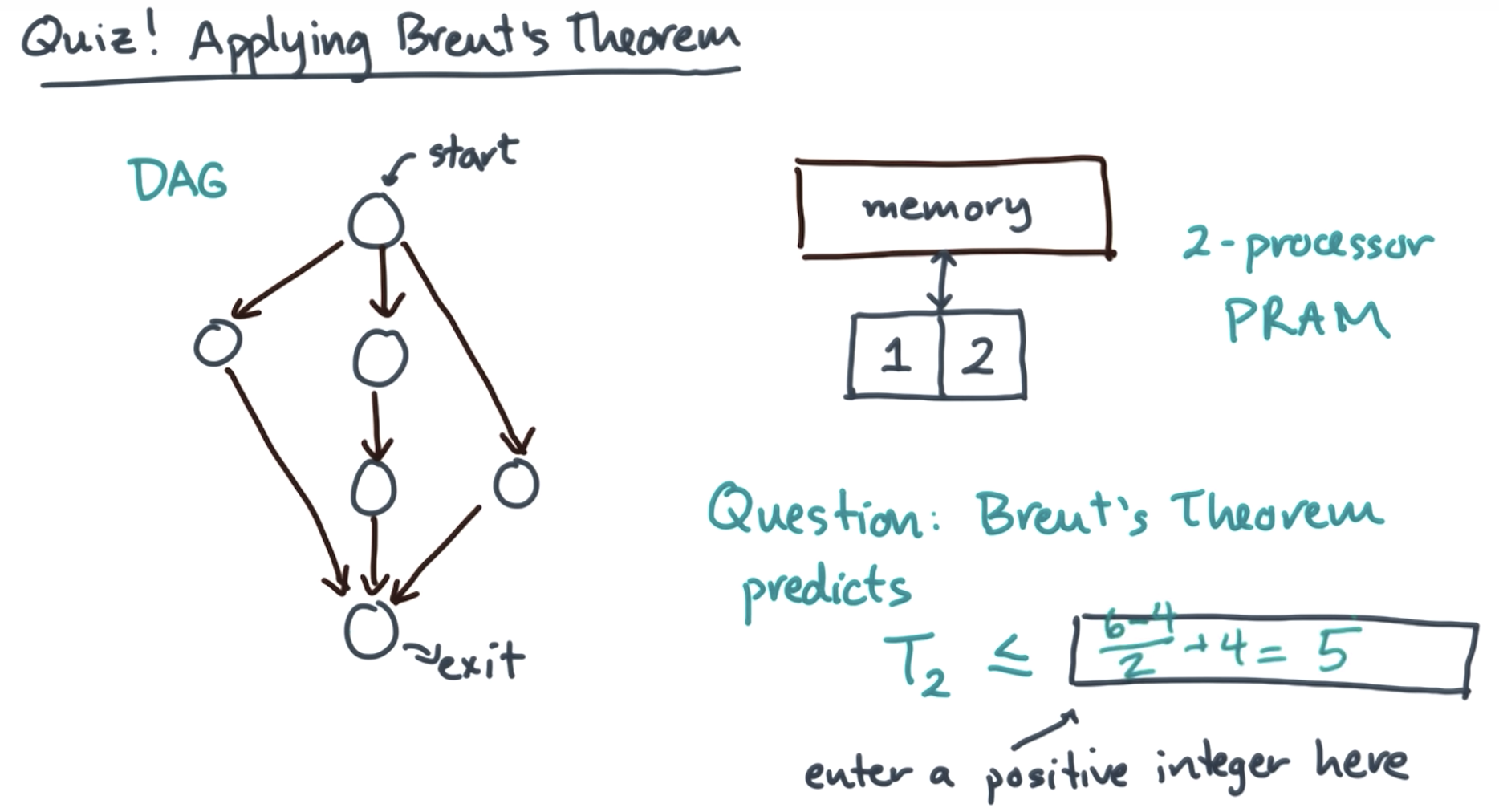
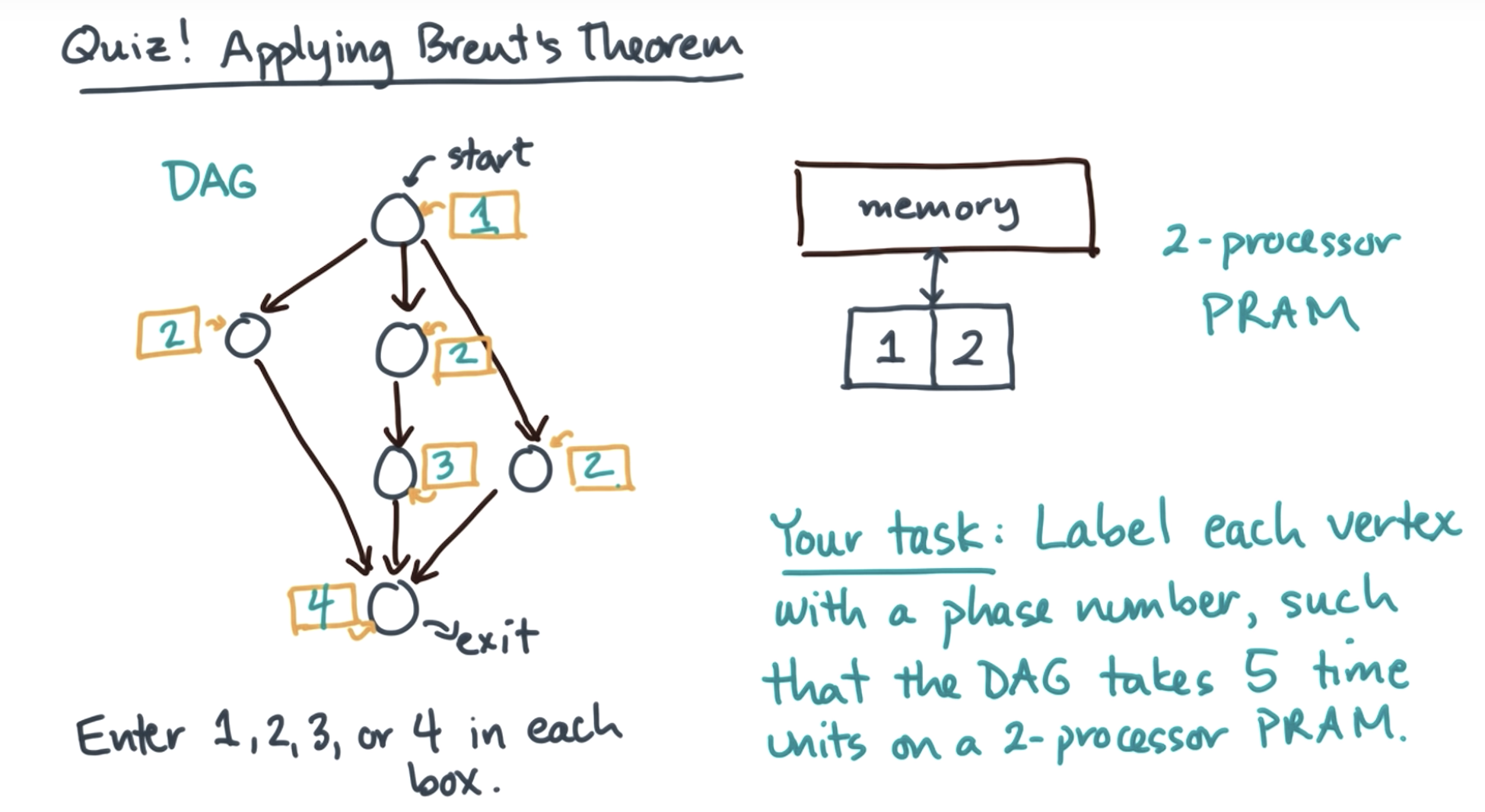
brent's theorem:

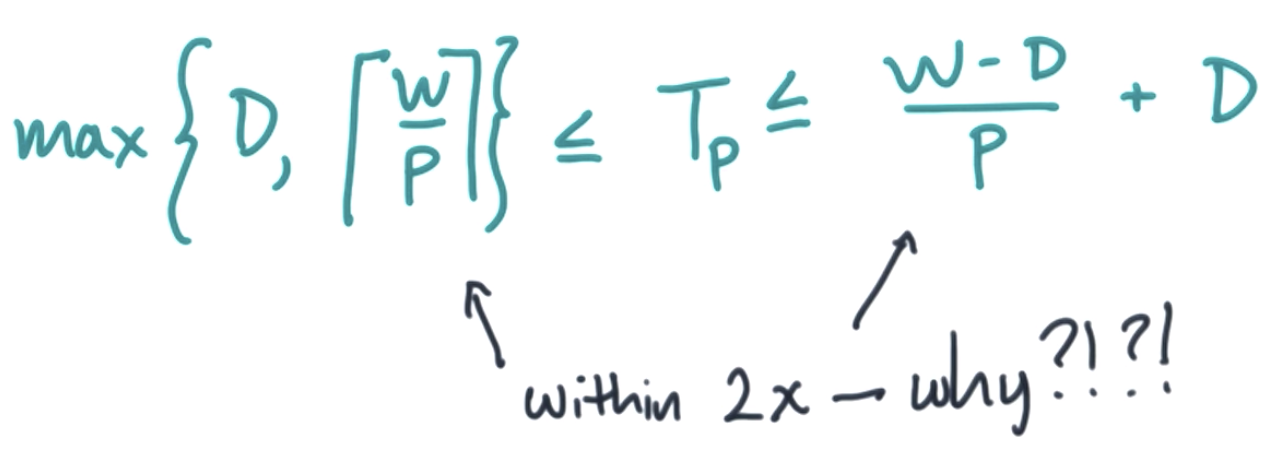
https://crd-legacy.lbl.gov/~dhbailey/dhbpapers/twelve-ways.pdf



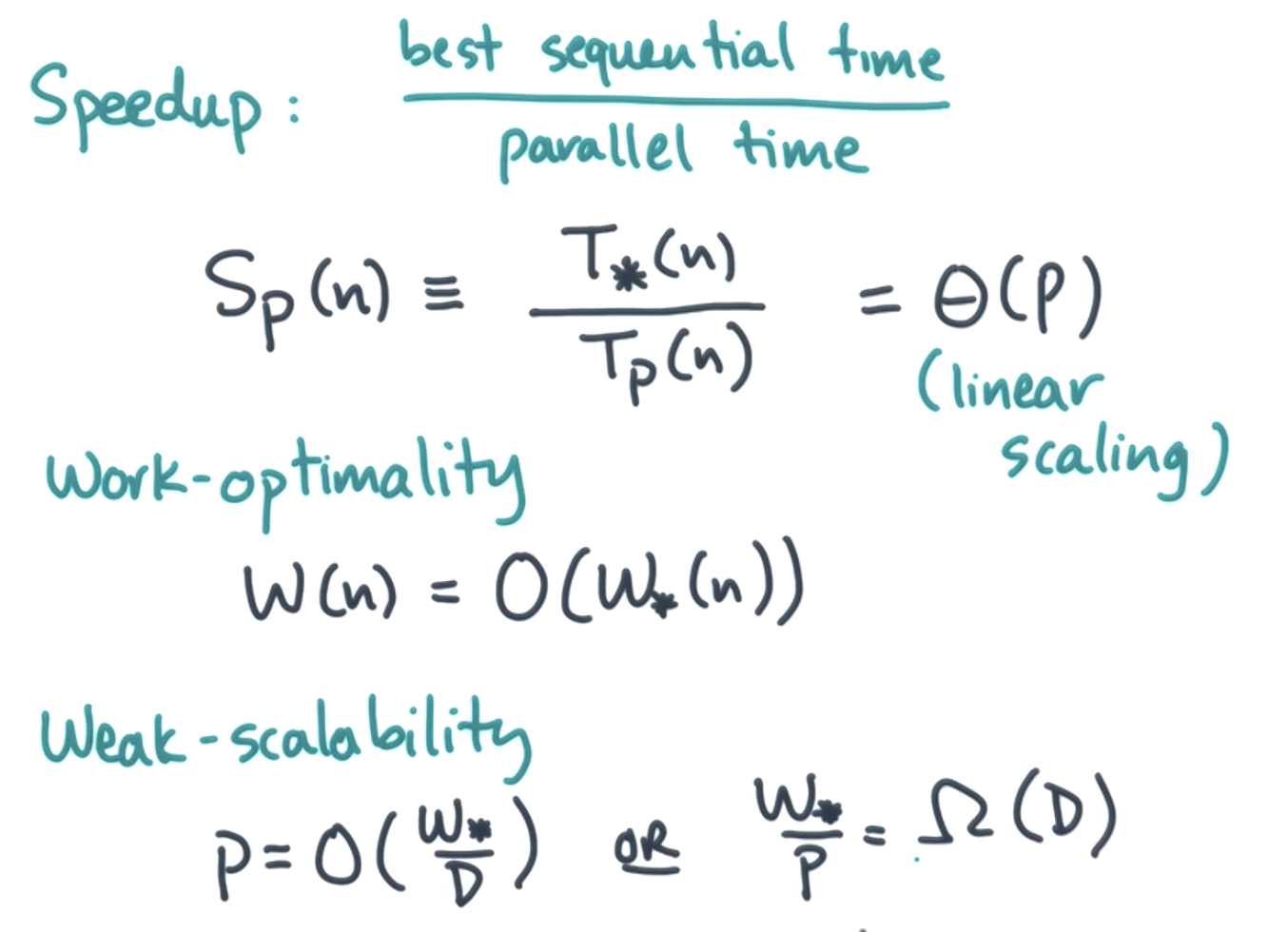

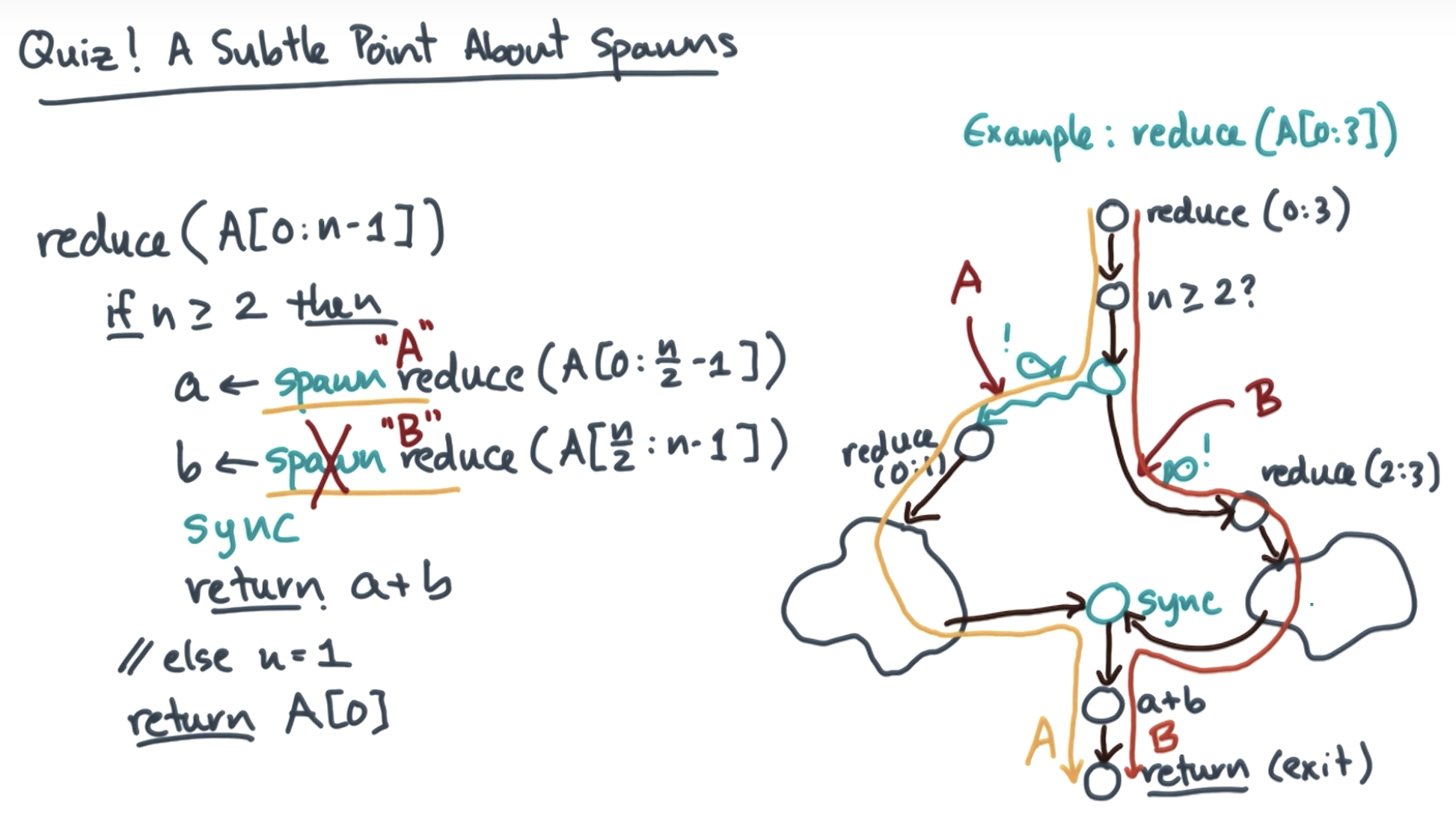
The correct answer depends on the situation.




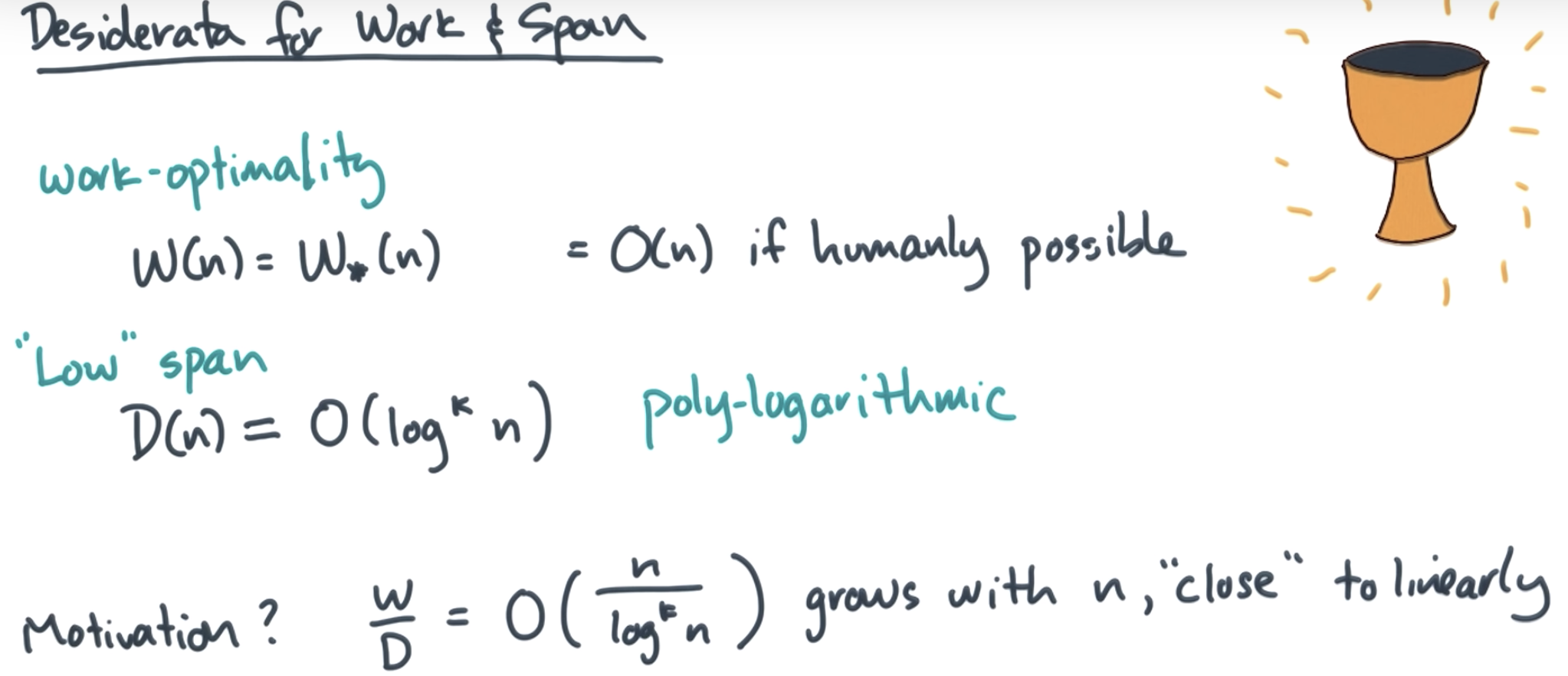
The Holy Grail for span is to find a poly-logarithmic algorithm




replace par-for with a procedure call


for i loop, the y[i]s are independent from each other
but for j loop, every component depends on y[i]

eg

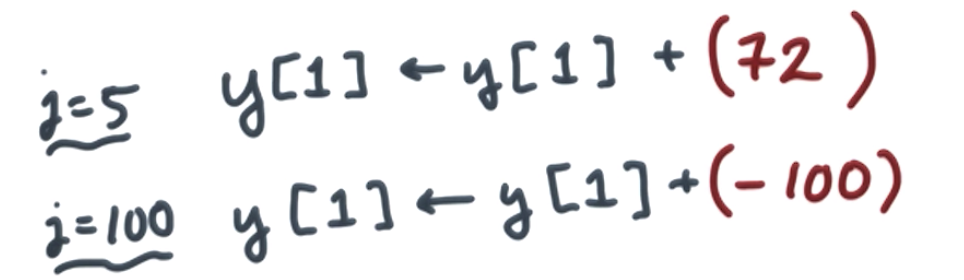

![]()


j loop is linear and executed by n times.


t[:] ← A[i,:] cdot x[:]
linear work and logarithmic span (look at the forth slide of this page)

https://www.cprogramming.com/parallelism.html

