剑指Offer面试题：19.包含Min函数的栈

一、题目：包含Min函数的栈

题目：定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的min函数。在该栈中，调用min、push及pop的时间复杂度都是O(1)。

　　这里我们要实现的就是min、push以及pop三个方法：

    public class MinInStack<T> where T : struct
    {
        private Stack<T> dataStack;
        private Stack<T> minStack;

        public MinInStack()
        {
            this.dataStack = new Stack<T>();
            this.minStack = new Stack<T>();
        }

        public bool IsEmpty()
        {
            return this.dataStack.Count == 0;
        }

        public T Top()
        {
            return this.dataStack.Peek();
        }

        public void Push(T item)
        {
        }

        public T Pop()
        {
        }

        public T Min()
        {
        }
    }

二、解题思路

2.1 核心步骤

　　把每次的最小元素（之前的最小元素和新压入栈的元素两者的较小值）都保存起来放到另外一个辅助栈里。下图展示了栈内压入3、4、2、1之后接连两次弹出栈顶数字再压入0时，数据栈、辅助栈和最小值的状态。

　　从表中我们可以看出，如果每次都把最小元素压入辅助栈，那么就能保证辅助栈的栈顶一直都是最小元素。

2.2 代码实现

　　（1）Push方法

    public void Push(T item)
    {
        // 把新元素添加到数据栈
        dataStack.Push(item);
        // 当新元素比之前的最小元素小时，把新元素插入辅助栈里；
        // 否则把之前的最小元素重复插入辅助栈里
        if (minStack.Count == 0 || item.CompareTo(minStack.Peek()) < 0)
        {
            minStack.Push(item);
        }
        else
        {
            minStack.Push(minStack.Peek());
        }
    }

　　（2）Pop方法

    public T Pop()
    {
        T item = dataStack.Pop();
        if(minStack.Count > 0)
        {
            minStack.Pop();
        }

        return item;
    }

　　（3）Min方法

    public T Min()
    {
        return minStack.Peek();
    }

三、单元测试

3.1 测试用例

    [TestMethod]
    public void MinTest1()
    {
        MinInStack<int> stack = new MinInStack<int>();
        stack.Push(3);
        Assert.AreEqual(stack.Min(),3);
    }

    [TestMethod]
    public void MinTest2()
    {
        MinInStack<int> stack = new MinInStack<int>();
        stack.Push(3);
        stack.Push(4);
        Assert.AreEqual(stack.Min(), 3);
    }

    [TestMethod]
    public void MinTest3()
    {
        MinInStack<int> stack = new MinInStack<int>();
        stack.Push(3);
        stack.Push(4);
        stack.Push(2);
        Assert.AreEqual(stack.Min(), 2);
    }

    [TestMethod]
    public void MinTest4()
    {
        MinInStack<int> stack = new MinInStack<int>();
        stack.Push(3);
        stack.Push(4);
        stack.Push(2);
        stack.Push(3);
        Assert.AreEqual(stack.Min(), 2);
    }

    [TestMethod]
    public void MinTest5()
    {
        MinInStack<int> stack = new MinInStack<int>();
        stack.Push(3);
        stack.Push(4);
        stack.Push(2);
        stack.Push(3);
        stack.Pop();
        Assert.AreEqual(stack.Min(), 2);
    }

    [TestMethod]
    public void MinTest6()
    {
        MinInStack<int> stack = new MinInStack<int>();
        stack.Push(3);
        stack.Push(4);
        stack.Push(2);
        stack.Push(3);
        stack.Pop();
        stack.Pop();
        Assert.AreEqual(stack.Min(), 3);
    }

    [TestMethod]
    public void MinTest7()
    {
        MinInStack<int> stack = new MinInStack<int>();
        stack.Push(3);
        stack.Push(4);
        stack.Push(2);
        stack.Push(3);
        stack.Pop();
        stack.Pop();
        stack.Pop();
        Assert.AreEqual(stack.Min(), 3);
    }

    [TestMethod]
    public void MinTest8()
    {
        MinInStack<int> stack = new MinInStack<int>();
        stack.Push(3);
        stack.Push(4);
        stack.Push(2);
        stack.Push(3);
        stack.Pop();
        stack.Pop();
        stack.Pop();
        stack.Push(0);
        Assert.AreEqual(stack.Min(), 0);
    }

3.2 测试结果

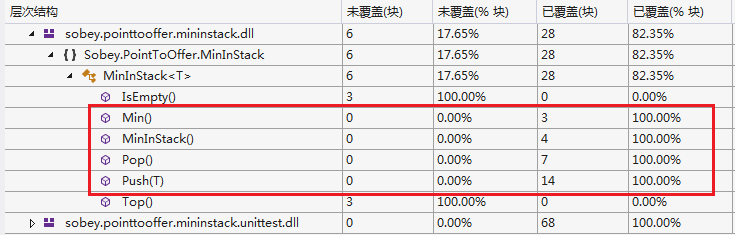
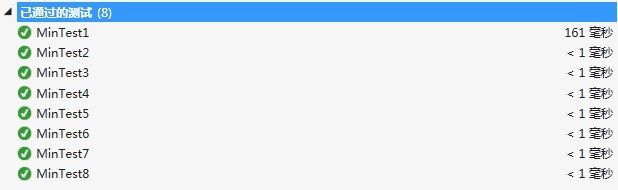
　　（1）测试通过情况

　　（2）代码覆盖率

作者：周旭龙

出处：http://edisonchou.cnblogs.com

本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文链接。