0.PTA得分截图
1.本周学习总结
1.1 总结树及串内容
1.1.1串
(1)串的定义:串(string)是由零个或多个字符组成的有限序列,又名叫字符串。一般记为s="a1a2...an",其中,s是串的名,用双引号括起来的字符序列是串的值;ai (1≤i≤n)可以是字母、数字或其他字符;串中字符的数目n成为串的长度。零个字符的串称为空串(null string),它的长度为0,可以直接用双引号“""”表示。串
串对于线性表的操作有很大区别,线性表更关注的是单个元素的操作,比如查找一个元素,插入或删除一个元素,但串中更多的是查找子串位置、得到指定位置子串、替换子串等操作。
(2)串的bf算法
假设从主串S="abcabcba"中,找到子串T="abcba"的位置,需要以下步骤
①主串S第一位开始,S与T前三位“abc”匹配成功,但第四个字母不一样,第一位匹配失败。

②主串S第二位开始,主串S首字母是b,T是a,失败

③主串S第三位开始,主串S首字母是c,T是a,失败

④主串S第四位开始5个字母全匹配,成功

这个算法就是对主串的每一个字符作为子串开头,与要匹配的字符串进行匹配,对主串进行大汛换,每个字符开头做T长度的小循环,直到匹配成功或全部遍历完成为止。
int BF(char S[],char T[])
{
int index=0;
int i=0;
int j=0;
while(S[i]!='\0'&&T[j]!='\0')
{
if(S[i]==T[j])//如果匹配成功,则继续比较下一对字符
{
i++;
j++;
}
else//如果匹配不成功,主串和子串回溯坐标。index记录的是每次匹配时的开始位置
{
index++;
i=index;
j=0;
}
}
if(T[j]=='\0') return index+1;
else return 0;
}
(3)串的kmp算法
void getnext(String T, int* next)
{
int i, j;
i = 1;
j = 0;
next[1] = 0;
while (i < T[0]) /*T[0]表示串T的长度*/
{
if (j == 0 || T[i] == T[j])/*T[i]表示后缀的单个字符*/
/*T[j]表示前缀的单个字符*/
{
i++;
j++;
next[i] = j;
}
else
j = next[j];/*若字符不相同,则j值回溯*/
}
}
这段代码目的是为了计算出当前要匹配的串T的next数组
/*返回子串T在主串S中第pos个字符之后的位置。若不存在,则函数返回值为0。*/
int KMP(String S, String T,int pos)
{
int i = pos; /*i 用于主串S当前位置下标值,若pos不为1,则从pos位置开始匹配 */
int j = 1; /*j 用于子串T中当前位置下标值*/
int next[255]; /* 定义一next数组*/
getnext(T, next); /*对串工作分析,得到next数组*/
while (i <= S[0] && j <= T[0]) /*若i小于S的长度且j小于T的长度时,循环继续*/
{
if (j == 0 || S[i] == T[j])
{
i++;
j++;
}
else /*指针后退重新开始匹配*/
j = next[j]; /* j退回合适的位置,i值不变*/
}
if (j > T[0])
return i - T[0];
else
return 0;
}
1.1.2树
(1)二叉树的存储结构
二叉树是非线性结构,其存储结构可以分为两种,即顺序存储结构和链式存储结构。
顺序存储结构:二叉树的顺序存储,就是用一组连续的存储单元存放二叉树中的结点。即用一维数组存储二叉树中的结点。
因此,必须把二叉树的所有结点安排成一个恰当的序列,结点在这个序列中的相互位置能反映出结点之间的逻辑关系。用编号的方法从树根起,自上层至下层,每层自左至右地给所有结点编号。依据二叉树的性质,完全二叉树和满二叉树采用顺序存储比较合适,树中结点的序号可以唯一地反映出结点之间的逻辑关系,这样既能够最大可能地节省存储空间,又可以利用数组元素的下标值确定结点在二叉树中的位置,以及结点之间的关系。
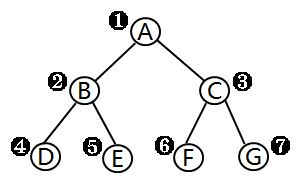
将这棵二叉树存入到数组中,相应的下标对应其同样的位置:

但是对于一般的非完全二叉树来说,如果仍然按照从上到下、从左到右的次序存储在一维数组中,则数组下标之间不能准确反映树中结点间的逻辑关系,可以在非完全二叉树中添加一些并不存在的空结点使之变成完全二叉树,(把不存在的结点设置为“^”)不过这样做有可能会造成空间的浪费,如下图所示,然后再用一维数组顺序存储二叉树。
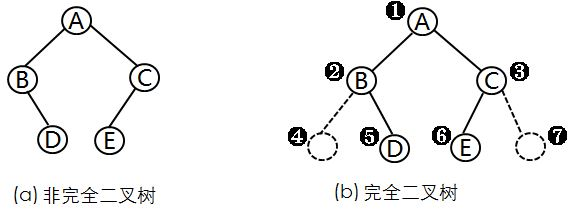

缺点是:有可能对存储空间造成极大的浪费,在最坏的情况下,一棵深度为k的右斜树,它只有k个结点,却需要2^k-1个结点存储空间。这显然是对存储空间的严重浪费,所以顺序存储结构一般只用于完全二叉树或满二叉树。
链式存储结构:二叉树的链式存储结构是指用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。
二叉树的每个结点最多有两个孩子,因此,每个结点除了存储自身的数据外,还应设置两个指针分别指向左、右孩子结点。如图,其中data是数据域,lchild和rchild都是指针域,分别存放指向左孩子和右孩子的指针。

(2)二叉树遍历
1.前序遍历
规则是若二叉树为空,则空操作返回,否则先访问根结点,然后前序遍历左子树,再前序遍历右子树。
/*二叉树的前序遍历递归算法*/
void PreOrderTraverse(BiTree T)
{
if(T == NULL)
return;
printf("%c",T->data);/*显示结点数据,可以更改为其他对结点操作*/
PreOrderTraverse(T->lchild); /*再先序遍历左子树*/
PreOrderTraverse(T->rchild); /*最后先序遍历右子树*/
}
2.中序遍历
规则是若树为空,则空操作返回,否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树。
/*二叉树的中序遍历递归算法*/
void InOrderTraverse(BiTree T)
{
if(T == NULL)
return;
InOrderTraverse(T->lchild); /*中序遍历左子树*/
printf("%c",T->data);/*显示结点数据,可以更改为其他对结点操作*/
InOrderTraverse(T->rchild); /*最后中序遍历右子树*/
}
3.后序遍历
规则是若树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后是访问根结点。
/*二叉树的中序遍历递归算法*/
void PostOrderTraverse(BiTree T)
{
if(T == NULL)
return;
PostOrderTraverse(T->lchild); /*后序遍历左子树*/
PostOrderTraverse(T->rchild); /*后序遍历右子树*/
printf("%c",T->data);/*显示结点数据,可以更改为其他对结点操作*/
}
4.层序遍历
规则是若树为空,则空操作返回,否则从树的第一层,也就是根结点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问。
1.2.谈谈你对树的认识及学习体会。
通过对树这一章的学习,发现树这一结构的复杂性和变化的多样性是前面的线性表无法比拟的,在数据结构中算是较重要的一部分。其中,二叉树是最重要的一种树,二叉树存储结构、建法、遍历及应用等知识都需要好好掌握,递归在建立和遍历二叉树中都有着广泛应用。