关于electron的基本调试

介绍

调试是开发中必不可少的一个过程，electron分为主进程和渲染进程，所以需要有分别调试这两个进程

 

渲染进程调试

electron渲染进程的调试跟web开发的调试过程差不多一样，因为这个进程相当于Chromium 的一个窗口，在开发环境中可以设置：win.webContents.openDevTools() 来打开devtools来调试代码。

 

接下来就可以对渲染进程进行调试，

 

vue-devtools

通常我们是使用vue+electron的模式进行开发，而在平时vue开发中，我们通常使用vue-devtools进程代码的调试，那么在electron中，我们就要想办法去加载vue-devtools这个插件

在electron-builder这个模板中提供了installVueDevtools这个模块去加载vue-devtools

import {installVueDevtools } from "vue-cli-plugin-electron-builder/lib"
...
app.on("ready",()=>{
   if(isDevelopment && !process.env.IS_TEST) {
   // Install Vue Devtools
       try {
         await installVueDevtools()
        }catch (e) {
         console.error('Vue Devtools failed to install:', e.toString())
    }
  }
})

然而这个installVueDevtools需要上网，才能下载vueDevtool到本地，所以我们需要另外一个版本，经过多方面的尝试，得到如下这种办法，首先下载在git下载vue-devtools编译后，把编译的文件放到项目如图：

 

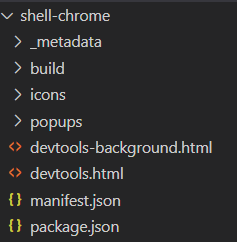
然后在通过electron的session模块加载

session.defaultSession.loadExtension(
      path.resolve(__dirname, "../shell-chrome")
    ).catch(e => {
      console.error("Vue Devtools failed to install:", e.toString());
    }).then(e => console.log(e));

效果如下

 

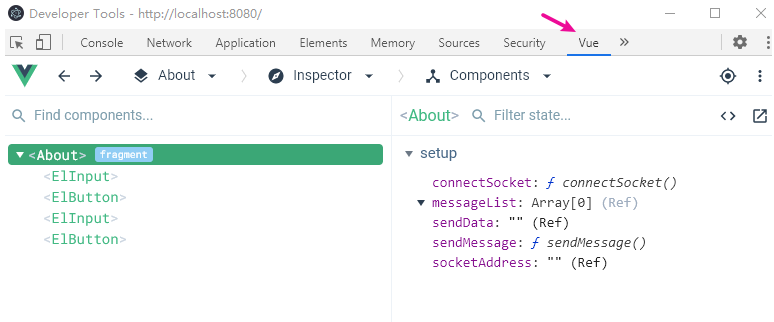
主线程调试

需要配置vscode，打开vscode的debug 添加 配置

{
    "version": "1.3.0",
    "configurations": [
      {
        "name": "Debug Main Process",
        "type": "node",
        "request": "launch",
        "cwd": "${workspaceFolder}",
        "runtimeExecutable": "${workspaceFolder}/node_modules/.bin/electron",
        "program": "${workspaceFolder}/src/main.ts",
        "protocol": "inspector",
        "args" : ["."]
      }
    ]
  }

不过有点坑的是不支持import的需要是用require才行不然会报错：

 

所以基本上我是使用console.log来调试

 

总结

electron的调试基本是这些，虽然很简单，但是也有不少人不知道的，特别是vue-devtools