惯例开始的废话
真的不开学了吗,家里蹲一学期?顶不住了

作业part2
第三章写过了,就写写第四章的学习笔记吧
第四章主线
生成模型
- 第三章主要介绍的贝叶斯决策是生成模型,而生成模型有优势,但是也有诸多的劣势
譬如高纬需要大量样本,但是随着维度的升高,样本的量是指数级增长。所以对于一些复杂情况,就需要判别模型。
判别模型不仅不需要大量的样本,而且还省去了观测似然概率的估计
然后介绍了线性判据,代入判别表达式,fx<0和fx>0为两类,
但是运用条件肯定是两类或者多类要线性可分,如果线性不可分的情况,那么线性判据就失效了。
一般线性判据,如果是二维,就是直线,三维是平面,高纬就是超平面
而其中两个重要参数w和w0,就是主要要求得的参数,得到之后,线性分类器也就得到了
解域的概念
而在学习的过程中,首先的问题就是解域
这两个参数的解究竟在哪个范围,确定了范围再求出最优解
也就是在解域中求得最优解
并行感知机or串行感知机
*首先对于数据预处理,使两类在超平面的同一侧
*并行感知机和串行感知机是以样本的给出方式划分的,样本一次全部给出称为并行,一个一个给出称为串行
而使用的求解w和w0的算法类似,而且目标函数都是一致的,也就是目的都是一致的,使得被错误分类的样本尽可能少
并行感知机
并行感知机的算法是,目标函数对于参数求偏导,当偏导数为0,则求得极值。
当然要求目标函数是凸函数或者凹函数,不然会出现求得的值并不是最优解的情况。
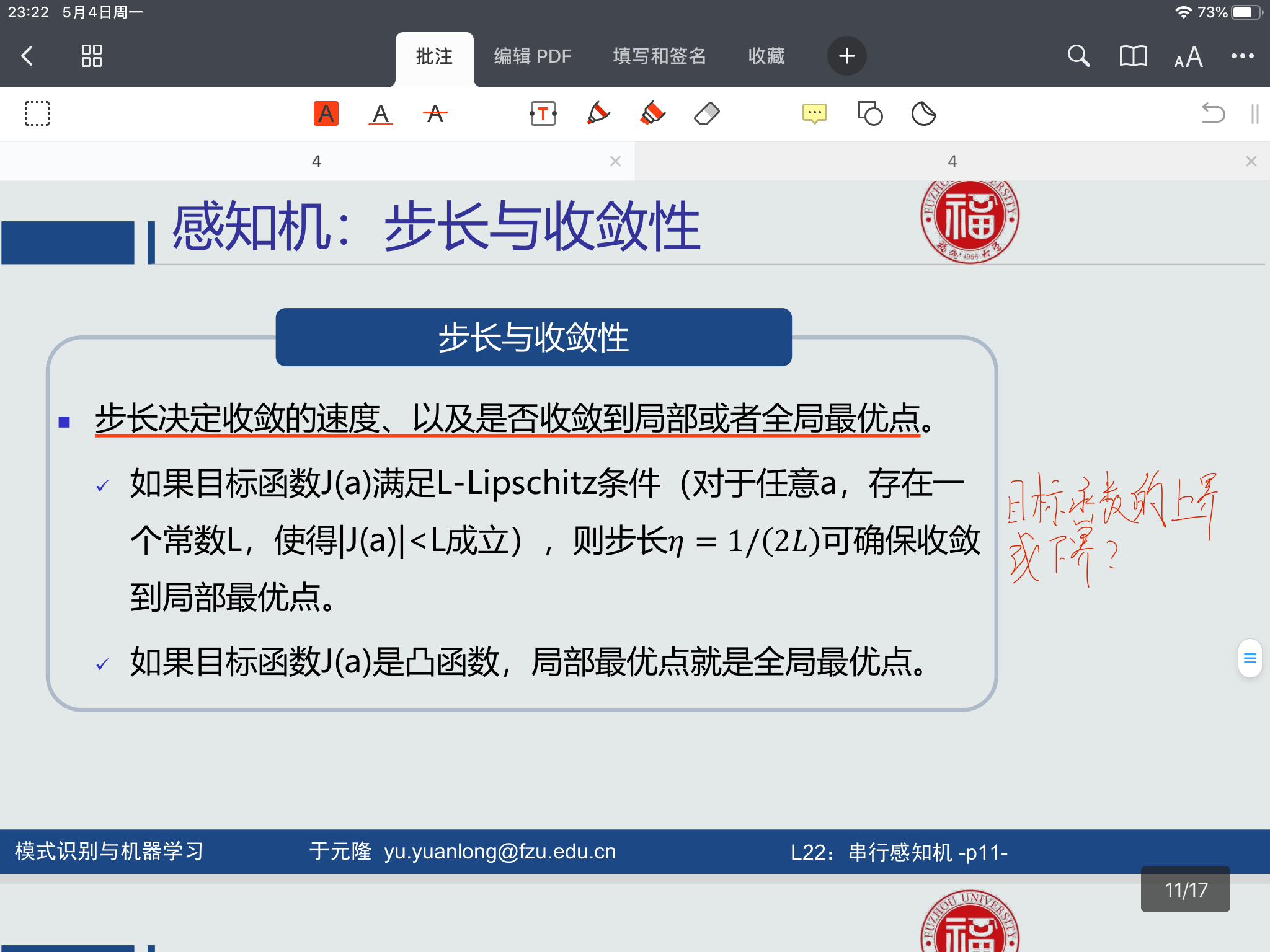
而并行感知机算法中的参数的求解使用的是梯度下降法,其中步长的选取很重要
步长小了,迭代次数很多,学习很慢,步长大了,会越过极值点,产生震荡。
而迭代过程的停止条件,所有训练样本代入判别函数,都>0
或者更新的目标函数值小于某个可以接受的误差值
更常用的一种方法是迭代一定的次数就停止
串行感知机
目标函数和并行感知机相同
而算法也类似,只是学习过程不太一致,是一个一个去学习样本,调整参数
感知机的收敛
也就是前面的说的最后求出的解,究竟是极值还是最值,这边给出了一个判据
感知机的泛化
加入约束条件,避免要求解的参数为0
好像没有正面,我也不懂为什么,QWQ
Fisher判据
这个,在我的理解中,是一种不同的找出线性判据的方法而已,算是数据清洗吧,我觉得
主要就是利用一些方法进行降维,然后尽量增大类间距离(类间散度),减小类内距离(类内散度)
其中的目标函数也是根据这个思路设计的,然后求解思路还是目标函数对待求参数求偏导,差不多
支持向量机
大概设计用来和Fisher差不多,也是增大类间散度吧,我觉得目的是相近的
但是方法有差异,支持向量机,是选两类中距离决策边界最大的训练样本,使这两个向量距离尽可能大,来达到增大类间散度的目的。这两个向量被称作支持向量。
而目标函数当然就是,这个距离d。
但是还存在着约束条件,就是样本代入判别函数,大于1(对数据和判别函数进行了处理,所以不是大于0),也就是能够对所有样本进行正确分类。然后就涉及到了,约束条件下的最优求解问题。
拉格朗日乘数法
这个方法,我记得大一高数就学过,用来求解条件下的最优解
而这里的方法是同样的,将约束条件乘以变量,比如c
- 然后fx=目标函数+c*约束条件
- fx对x求偏导
- fx对c求偏导
这种方法,如果是多个约束条件,就对其余的约束条件做相同操作。
而使用的时候,要分不同的情况,所以需要提前求解出极值点,就是目标函数对x求偏导,使其为0 - 极值点在可行域内,则直接取极值点就可以
- 极值点在可行域边界,要在该点出,fx和gx负梯度方向相反
拉格朗日对偶问题
在拉格朗日问题中,可能会出现对于约束条件进行操作后,仍有约束条件的可能,也就是拉格朗日函数带有约束条件
那么就需要拉格朗日对偶法,进行求解
方法是求得主函数L的下界,然后求下界对约束条件系数的最大值
使用对偶函数还有另一个优点,就是对偶函数是凹函数,可以保证局部极值点就是全局极值点
支持向量机学习算法
这一节,主要就是使用拉格朗日对偶方法对支持向量机进行求解
求得最佳的w和w0
然后
然后就没了,线性模型是否可以用于回归问题
当然是可以的,但是老师没继续录了,gg