logistic regression用于二分类的情况。即Y∈{0,1}。
模型
对于分布形式如下的样本:
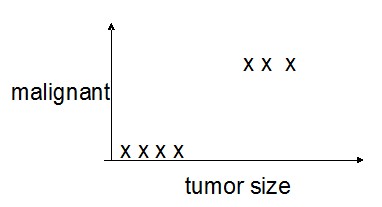
如果使用linear regression的话,可以拟合出一条类似下图的曲线:

通过增加一个阈值,我们也可以做二分类,例如,假定阈值为0.5:
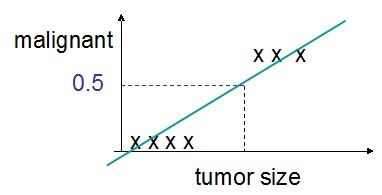
那么,可以写成:
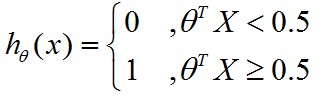
但是这种方式在面对类似这样的数据分布时,会有问题:
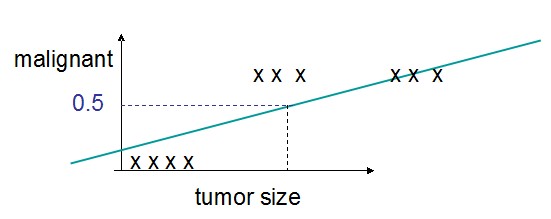
图中的回归线为了拟合到右边的3个奇异点而变得非常斜,这不是我们希望看到的。
为此,我们为logistic regression另外提出了一种模型:
linear regression的计算模型是:hθ(x)=θTx
logistic regression的计算模型是:hθ(x)=g(θTx)
注意:我们增加了一个g(z)函数,其中z=θTx
g(z)函数表示一个数据从0到1的分布,使得y∈(0,1)
一般的,我们取
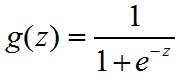
g(z)的图像为:
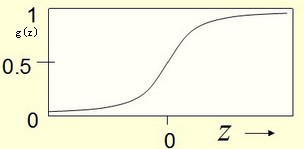
这里函数被称为sigmod函数,也称logistic函数。为什么要选择这样的函数,可以看 @老师木 写的【为什么我们喜欢用sigmoid这类S型非线性变换?】。
现在,我们的hθ(x)就变为了
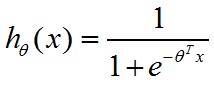
其中,θ为参数。hθ(x)∈[0,1]
惩罚函数 cost function
要对监督型模型进行训练,我们就需要一个cost函数来做penalty。在linear regression中,我们使用error square来做cost。但在现在模型下,如果使用error square的话,会使cost 函数变成一个非凸函数(non-convex),这样不容易进行optimization。
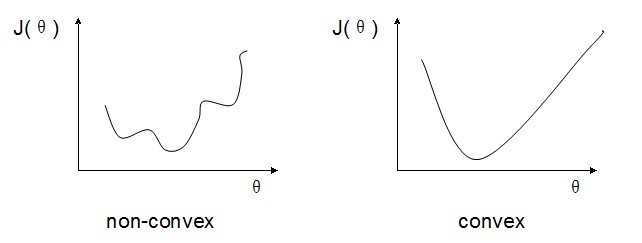
现在,我们假设只有一个样本,且y=1.
如果使用error square的方式的话,则有